$Project Greater Ed Logo$

What Integrals Are and the Fundamental Theorem of Calculus

Business Calculus Area, Continuous Accumulation, and Definite Integrals What Integrals Are and the Fundamental Theorem of Calculus

Estimating Areas Under Curves

Suppose we have the graph below and we want to know the exact area under the curve (technically its a line, but all graphs are usually called “curves” no matter what their shape is).

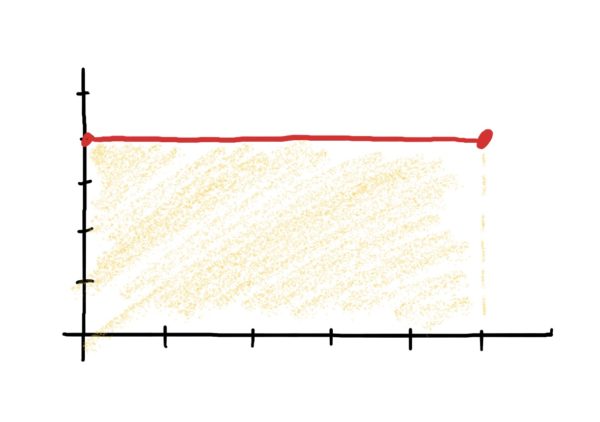
constant function with area underneath shaded

Clearly, one could apply the good ol’ area formula for quadrilaterals: $Length\cdot Width = Area$. It’s a fairly easy computation when the function is a flat line. However, suppose we have a more complicated graph, such as

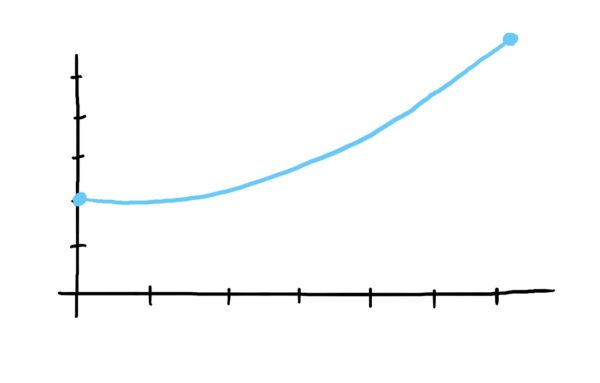
We don’t (yet) have a tidy way of computing the area under this curve. Maybe we can use boxes to estimate the area under the curve? Lets try it this way: Use six boxes of equal width (call this width $\Delta x$), and whose heights are dictated by where the top-left corner of each box touches the function.

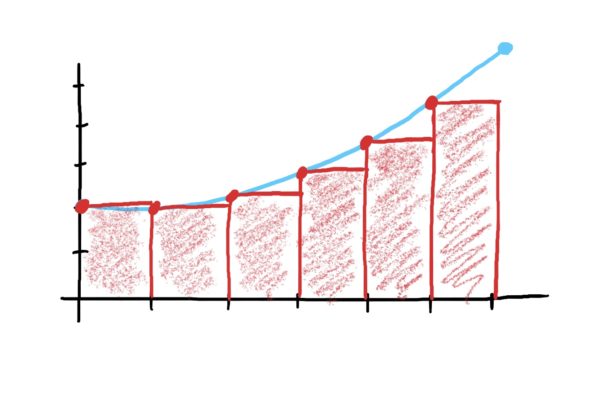
approximating the area under the curve using 6 boxes of equal width

Then, what we can do is add up the areas of each of these boxes to get the total area.

computation of all areas being added up to get the total area

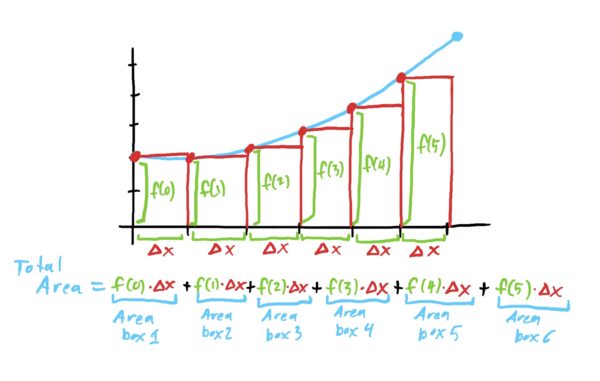
Notice, though, that this area is not the TRUE area under the curve; it is merely an estimate. There are gaps under our function that are not covered by our boxes, and so there is area that is “missing” from our calculations above.

What one can do to get a better approximation is drive up the number of boxes between the interval’s endpoints so you have many thin boxes, each of which touches the graph at its top-left endpoint.

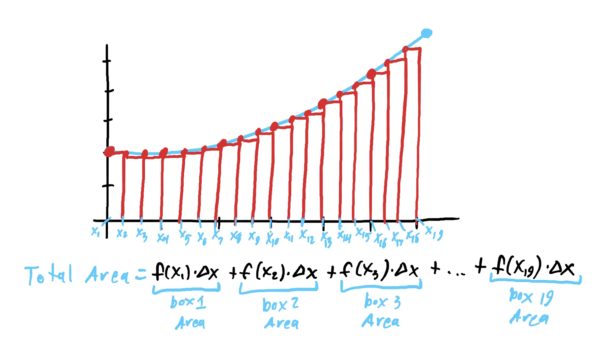
Approximating the area under the curve using many boxes

Still, even with many more boxes like in the above, we still only have an estimate – a really good estimate, but still an estimate – because we still have small little areas above each box that are unaccounted for. This would happen no matter how many boxes you use. But again, notice that the missing area is getting smaller and smaller when we use more boxes. So, as the number of boxes approaches infinity, the area estimate approaches the TRUE area under the curve. Sounds a lot like a limit! In fact, we have a special name and notation for this limit.

Definite Integral

Let $f$ be a continuous function (i.e. a function with no holes or jumps) defined on some interval $[a,b]$. The area under the the graph of $f$ on the interval $[a,b]$, called the definite integral of $f$ on $[a,b]$, denoted as $\int^b_a f(x)\ dx$, is given by the limit
$$\int^b_a f(x)\ dx=\lim_{n\rightarrow \infty}f(x_1)\cdot \Delta x+f(x_2)\cdot \Delta x+…+f(x_{n-1})\cdot \Delta x+f(x_n)\cdot \Delta x$$
where $\Delta x =\frac{b-a}{n}$ is the width of each box, and the $x_1$, $x_2$, etc. are the $x$-values of the top-left endpoints of each of your boxes.

You can think of the integral sign $\int$ as a “sexy letter ‘s’ ” which stands for “sum.” $f(x)$ represents the height of the box whose top-left endpoint is at $x$ and whose width is “$dx$”.

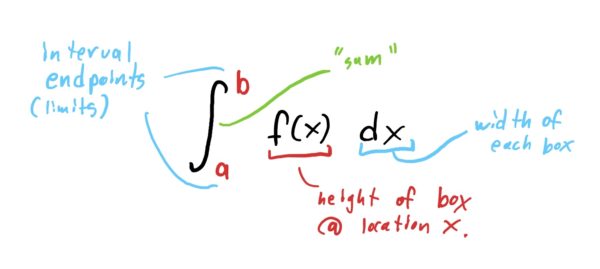
Note that is impractical or even impossible to compute areas under curves using this limit directly (though, computers tend to use similar approximation strategies). Thankfully, people far smarter than me figured out and proved the following result which makes computing integrals a lot easier!

Fundamental Theorem of Calculus

Let $f$ be a continuous function defined on interval $[a,b]$ and suppose that $f$ has antiderivative $F$. Then
$$\int^b_a f(x)\ dx = F(b)-F(a)$$

Basically, what this theorem is saying is: “Find an antiderivative of $f$, then plug in the endpoints of your interval $[a,b]$ and then subtract the results.” Super easy!

Note that the above theorem is technically “part 2” of a two-part “fundamental theorem of Calculus,” but it is usually the part that most often comes to mind when one thinks of said theorem.

What we are asked to compute is the area of the shaded region below the graph depicted below.

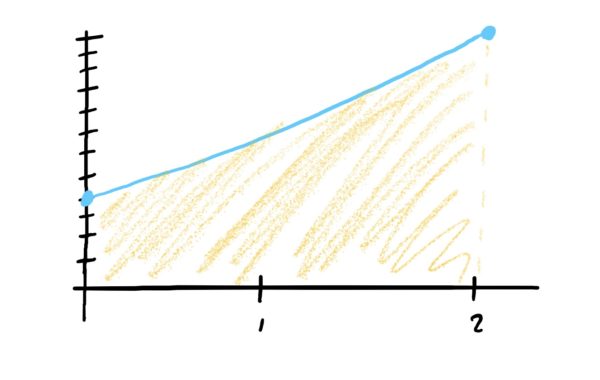
So, we use the fundamental theorem of calculus to pull this off. First, compute an antiderivative of $f$ and call it $F(x)$:

$$F(x) = \frac{x^3}{3}+x^2+4x$$

Then, plug in $b=2$ and $a=0$ into the above and subtract!

$$\begin{align}F(2)-F(0) &= (\frac{2^3}{3}+2^2+4)-(\frac{0^3}{3}+0^2+4)\\&=\frac{32}{3}-4\\&=\frac{20}{3}\end{align}$$

Yup. That easy.

Who Cares?

Integrals have a wide array of uses well beyond just finding area under a curve. Because, at its core, an integral is a tool for summing up many, many small things, it can also be used to find totals of things that happen over very short time frames (or other short measures). A quick example is given below to illustrate what I mean.

Totaling Over a Larger Timeframe with More Data

Suppose we have a similar problem of finding a company’s total number of sales over a 6-year period, where the number of sales (in millions) at any moment is modeled by a continuously changing function as graphed below, and given by the function \(f(x)=x^3-x^2+3.

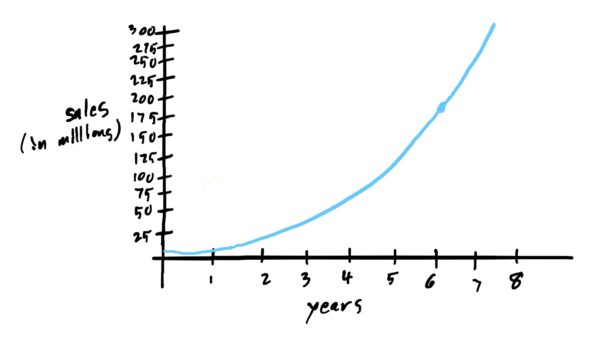
graph modeling sales from moment to moment over a 6-year timeframe

The company might be interested in the total number of sales from the start of the timeframe in question (i.e. where $x=0$). However, the problem is that the number of sales varies continuously. That is, the number of sales is different from minute-to-minute. There is thus just so much data that it would be impractical or impossible to add up all sales from minute-to-minute over the course of years. If we are thinking in terms of box areas, this would entail adding up MANY little box areas, all of equal (but tiny) width.

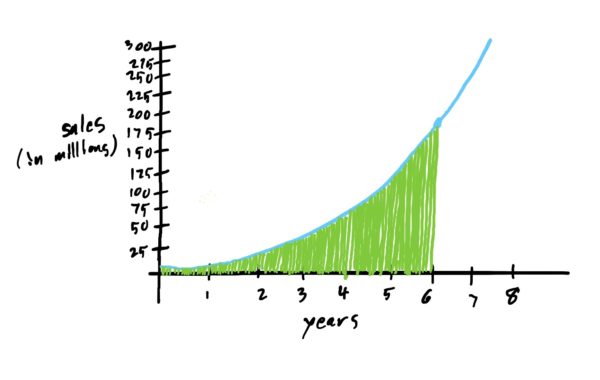
approximating the area under the curve using a bajillion little boxes

Since we are essentially asking for the total area under the curve conveniently given by a rule, we can just apply the fundamental theorem of calculus:

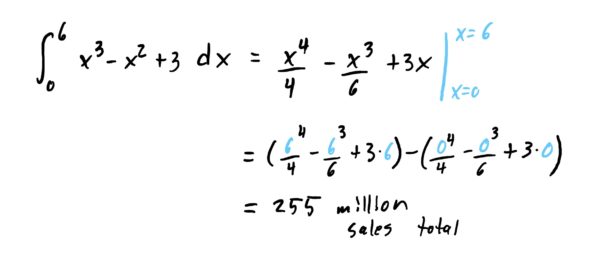
showing all the work of the integral computation which was explained above.

Thus, we get that the area under the curve, and thus the total number of sales from the start of year-$0$ to year-$6$ is $255$ million.

Compute the following areas

Try really hard! … jk….Start by taking the antiderivative of each term, then plug in your interval endpoints and subtract your results.

Calculating Areas and Definite Integrals (its the same for both):

Start by finding the antiderivative $F(x)$ of the stuff inside the integral
Find $F(b)$ by plugging in the upper limit (i.e. the thing in the superscript of the integral sign) into the antiderivative you found earlier
Find $F(a)$ by plugging in the lower limit into the antiderivative.
Compute $F(b)-F(a)$

Fundamental Theorem of Calculus (Part 2):

If $F(x)$ is an antiderivative of $f(x)$, then $\int^b_a f(x)\ dx=F(b)-F(a)$

Area$=\frac{7}{3}$

Note that the function $f(x)=1$ is flat with height 1. On the interval given, what shape does the graph of this function make?

Start by finding the antiderivative $F(x)$ of the stuff inside the integral
Find $F(b)$ by plugging in the upper limit (i.e. the thing in the superscript of the integral sign) into the antiderivative you found earlier
Find $F(a)$ by plugging in the lower limit into the antiderivative.
Compute $F(b)-F(a)$

Fundamental Theorem of Calculus (Part 2):

If $F(x)$ is an antiderivative of $f(x)$, then $\int^b_a f(x)\ dx=F(b)-F(a)$

Net Area$=4$

Start by taking the antiderivative of each term, then plug in your interval endpoints and subtract your results.

Start by finding the antiderivative $F(x)$ of the stuff inside the integral
Find $F(b)$ by plugging in the upper limit (i.e. the thing in the superscript of the integral sign) into the antiderivative you found earlier
Find $F(a)$ by plugging in the lower limit into the antiderivative.
Compute $F(b)-F(a)$

Fundamental Theorem of Calculus (Part 2):

If $F(x)$ is an antiderivative of $f(x)$, then $\int^b_a f(x)\ dx=F(b)-F(a)$

Net Area$=\frac{7}{6}$

Compute the following definite integrals

Start by taking the antiderivative of each term, then plug in your upper and lower limits, and subtract the results.

Calculating Areas and Definite Integrals (its the same for both):

Start by finding the antiderivative $F(x)$ of the stuff inside the integral
Find $F(b)$ by plugging in the upper limit (i.e. the thing in the superscript of the integral sign) into the antiderivative you found earlier
Find $F(a)$ by plugging in the lower limit into the antiderivative.
Compute $F(b)-F(a)$

Fundamental Theorem of Calculus (Part 2):

If $F(x)$ is an antiderivative of $f(x)$, then $\int^b_a f(x)\ dx=F(b)-F(a)$

$\int^1_{-1} 3x^2+x+1\ dx=4$

Start by taking the antiderivative of each term, then plug in your upper and lower limits, and subtract the results.

Calculating Areas and Definite Integrals (its the same for both):

Start by finding the antiderivative $F(x)$ of the stuff inside the integral
Find $F(b)$ by plugging in the upper limit (i.e. the thing in the superscript of the integral sign) into the antiderivative you found earlier
Find $F(a)$ by plugging in the lower limit into the antiderivative.
Compute $F(b)-F(a)$

Fundamental Theorem of Calculus (Part 2):

If $F(x)$ is an antiderivative of $f(x)$, then $\int^b_a f(x)\ dx=F(b)-F(a)$

$\int^1_{-1} 4\ dx=8$

Start by taking the antiderivative of each term, then plug in your upper and lower limits, and subtract the results.

Fundamental Theorem of Calculus (Part 2):

If $F(x)$ is an antiderivative of $f(x)$, then $\int^b_a f(x)\ dx=F(b)-F(a)$

Calculating Areas and Definite Integrals (its the same for both):

Start by finding the antiderivative $F(x)$ of the stuff inside the integral
Find $F(b)$ by plugging in the upper limit (i.e. the thing in the superscript of the integral sign) into the antiderivative you found earlier
Find $F(a)$ by plugging in the lower limit into the antiderivative.
Compute $F(b)-F(a)$

$\int^1_0 x^{1/2}\ dx=\frac{2}{3}$

First, convert radicals to fractional powers, then find the antiderivative.

Fundamental Theorem of Calculus (Part 2):

If $F(x)$ is an antiderivative of $f(x)$, then $\int^b_a f(x)\ dx=F(b)-F(a)$

Calculating Areas and Definite Integrals (its the same for both):

Start by finding the antiderivative $F(x)$ of the stuff inside the integral
Find $F(b)$ by plugging in the upper limit (i.e. the thing in the superscript of the integral sign) into the antiderivative you found earlier
Find $F(a)$ by plugging in the lower limit into the antiderivative.
Compute $F(b)-F(a)$

$\int^1_0 x^{\frac{1}{3}}+\sqrt{x}\ dx=\frac{17}{12}$

First, convert radicals to fractional powers, and bring powers of $x$ in denominators up to the numerators (making the exponent negative), then find the antiderivative.

Start by finding the antiderivative $F(x)$ of the stuff inside the integral
Find $F(b)$ by plugging in the upper limit (i.e. the thing in the superscript of the integral sign) into the antiderivative you found earlier
Find $F(a)$ by plugging in the lower limit into the antiderivative.
Compute $F(b)-F(a)$

Fundamental Theorem of Calculus (Part 2):

If $F(x)$ is an antiderivative of $f(x)$, then $\int^b_a f(x)\ dx=F(b)-F(a)$

$\int^4_1 3\sqrt{x}+\frac{1}{x^{1/2}}\ dx=16$

First, convert radicals to fractional powers, and bring powers of $x$ in denominators up to the numerators (making the exponent negative), then find the antiderivative.

Start by finding the antiderivative $F(x)$ of the stuff inside the integral
Find $F(b)$ by plugging in the upper limit (i.e. the thing in the superscript of the integral sign) into the antiderivative you found earlier
Find $F(a)$ by plugging in the lower limit into the antiderivative.
Compute $F(b)-F(a)$

Fundamental Theorem of Calculus (Part 2):

If $F(x)$ is an antiderivative of $f(x)$, then $\int^b_a f(x)\ dx=F(b)-F(a)$

$\int^4_1 \frac{1}{\sqrt{x} +\frac{5}{x^2}\ dx=\frac{23}{4}$

Previous Lesson

Back to Lesson

Next Topic