Using U-Sub with Exponential Functions
Recall How Derivatives of Exponents Work
Suppose \(f(x)=e^{x^2+1}\). How does one go about deriving this function?
First, we note that the exponent \(x^2+1\) is the “inside function” which is being plugged into \(e^x\). So, to derive this we need to use the chain rule. The work and result of this is shown below.
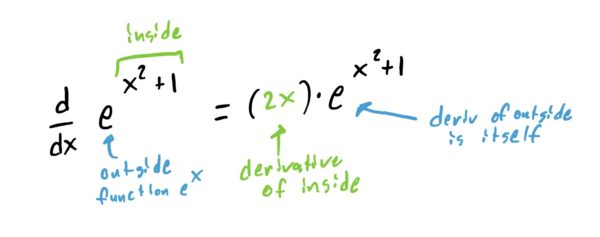
U-Sub With Exponentials
Suppose now that we are given the task of finding
$$\int 3x^2\cdot e^{x^3}\ dx$$
To find this indefinite integral, we can “undo” the chain rule using u-substitution, noting that the “inside function” that we will let be our \(u\) is the exponent \(x^3\). The full process for this is shown below.
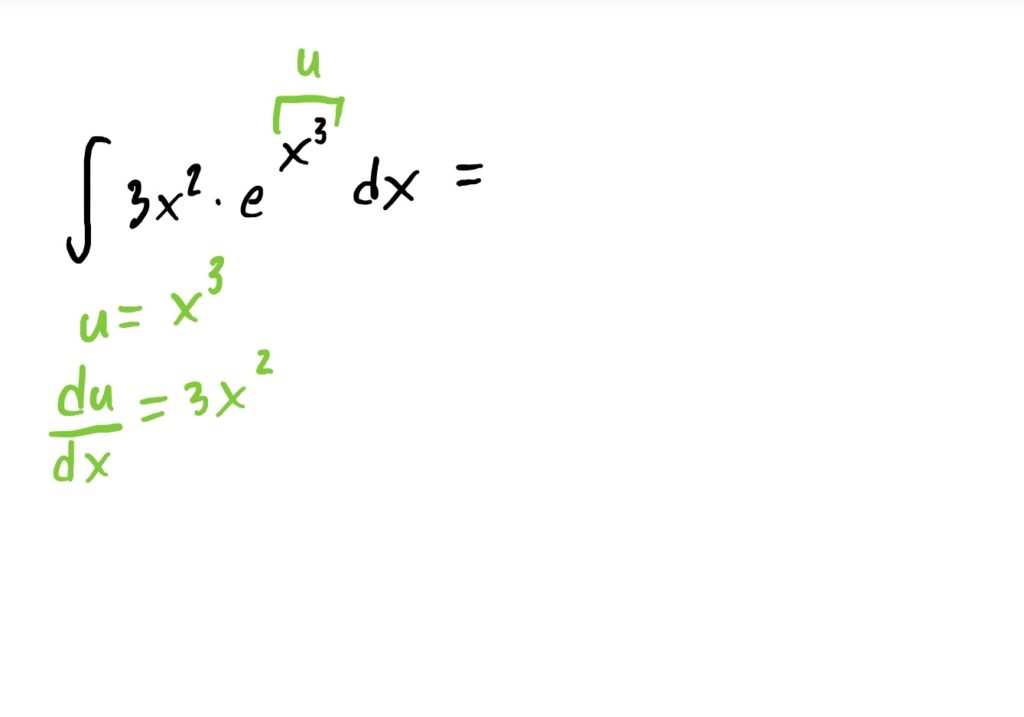
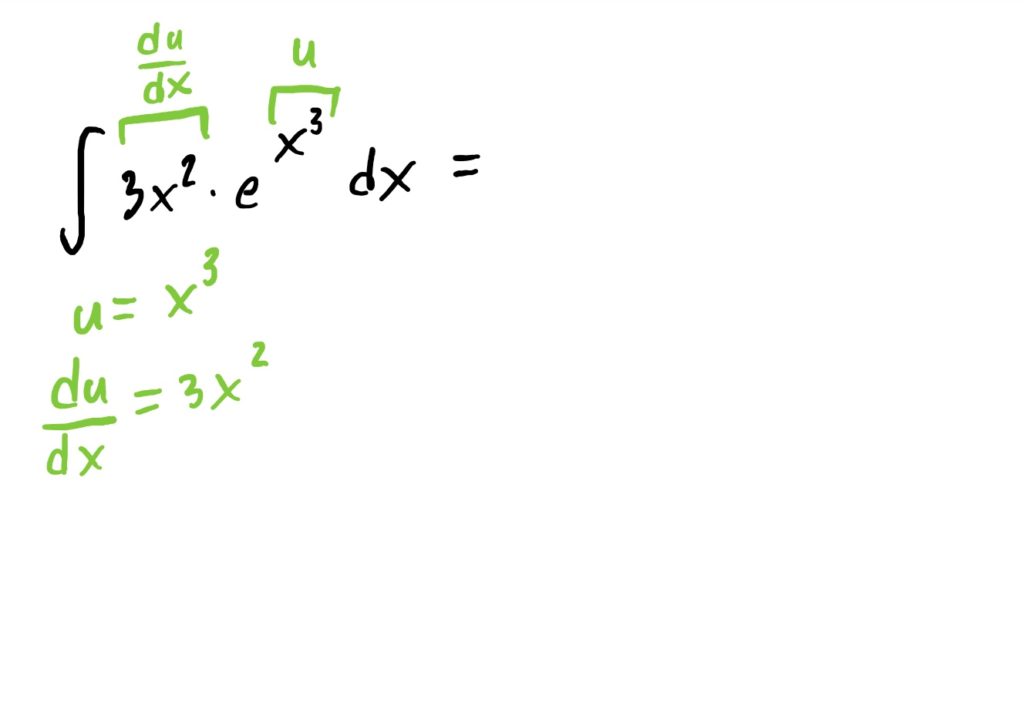
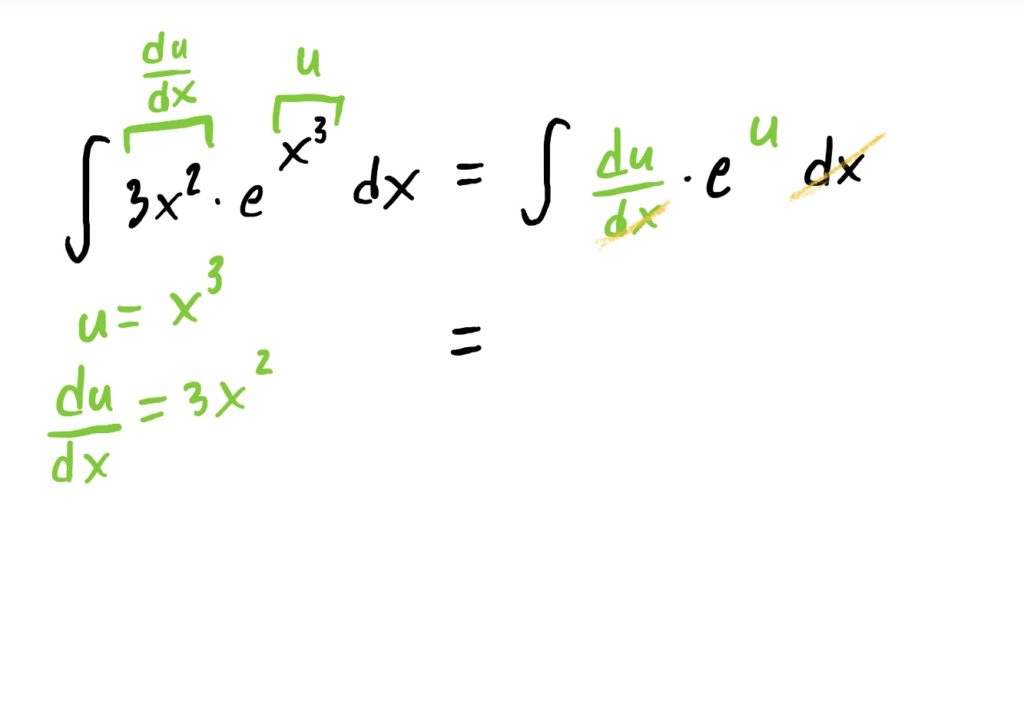
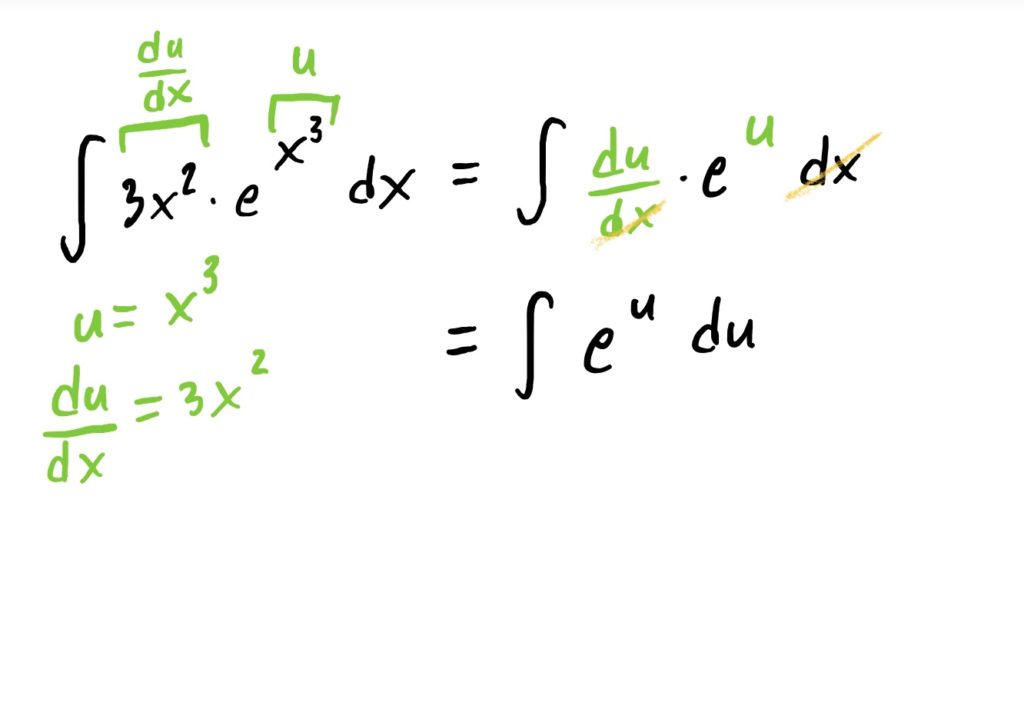
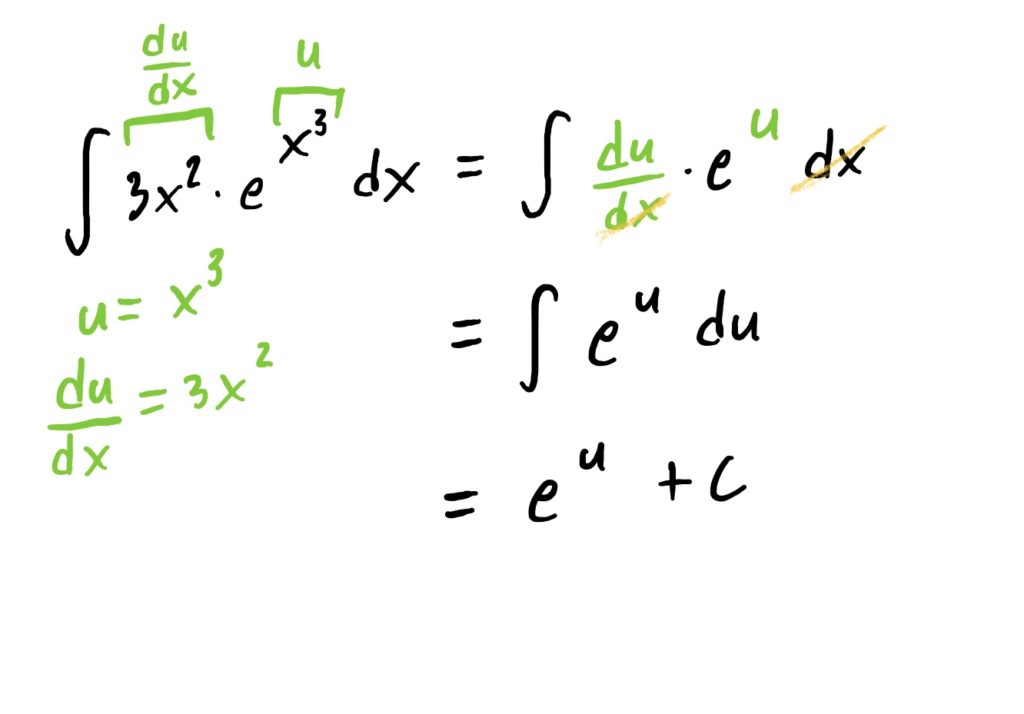
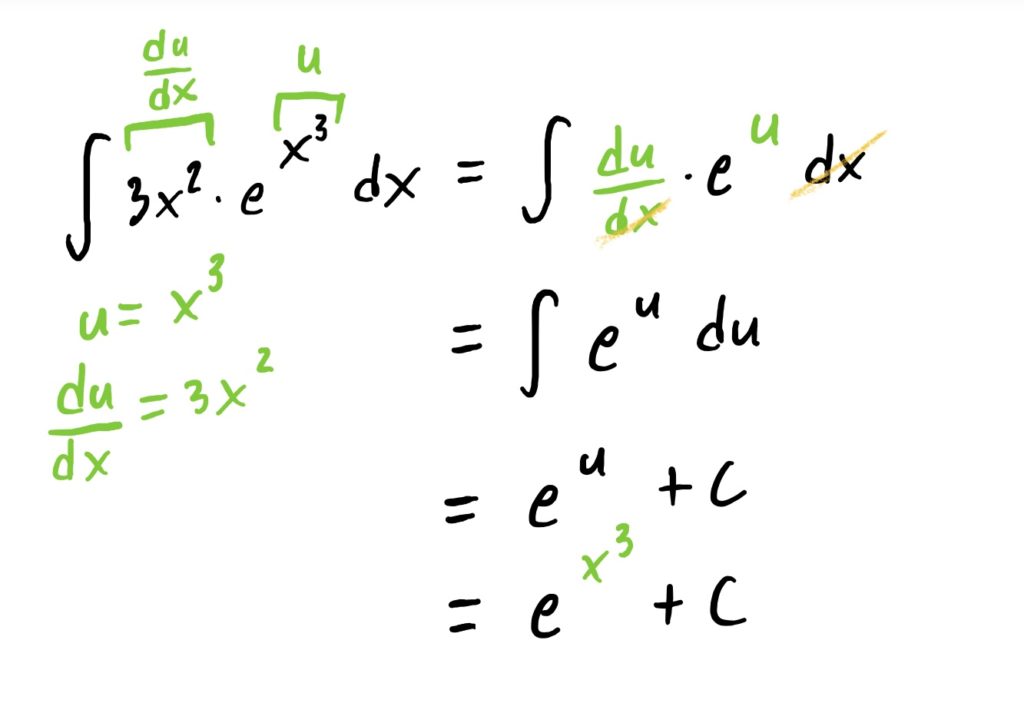
All of the problems you see below essentially work the same way. You might need to do a bit of algebraic manipulation of the \(\frac{du}{dx}\) equation so that you can carry out your substitution correctly.
Compute the following antiderivatives
Let \(u=x^2\).
- First find an “inside function” and let it be called \(u\).
- Find the derivative of \(u\), \(\frac{du}{dx}\)
- Find where the expressions you have for \(u\) and \(\frac{du}{dx}\) appear in the integral and replace them in the integrand with \(u\) and \(\frac{du}{dx}\). You may need to first rearrange the equations for \(u\) or \(\frac{du}{dx}\) before substituting. Your integral should have no \(x\)’s anymore after subbing.
- integrate as usual. Don’t forget “+C”
- plug back in your \(u\) formula and call it a day
- (If computing a definite integral, then plug in upper and lower limits in for \(x\), and subtract the results.)
\(e^{x^2}+C\)
Let \(u=2x^3+1\)
- First find an “inside function” and let it be called \(u\).
- Find the derivative of \(u\), \(\frac{du}{dx}\)
- Find where the expressions you have for \(u\) and \(\frac{du}{dx}\) appear in the integral and replace them in the integrand with \(u\) and \(\frac{du}{dx}\). You may need to first rearrange the equations for \(u\) or \(\frac{du}{dx}\) before substituting. Your integral should have no \(x\)’s anymore after subbing.
- integrate as usual. Don’t forget “+C”
- plug back in your \(u\) formula and call it a day
- (If computing a definite integral, then plug in upper and lower limits in for \(x\), and subtract the results.)
\(e^{2x^3+1}+C\)
Let \(u=x^2+x\).
- First find an “inside function” and let it be called \(u\).
- Find the derivative of \(u\), \(\frac{du}{dx}\)
- Find where the expressions you have for \(u\) and \(\frac{du}{dx}\) appear in the integral and replace them in the integrand with \(u\) and \(\frac{du}{dx}\). You may need to first rearrange the equations for \(u\) or \(\frac{du}{dx}\) before substituting. Your integral should have no \(x\)’s anymore after subbing.
- integrate as usual. Don’t forget “+C”
- plug back in your \(u\) formula and call it a day
- (If computing a definite integral, then plug in upper and lower limits in for \(x\), and subtract the results.)
\(e^{x^2+x}+C\)
Let \(u=(\ln(x)+1)^2\)
- First find an “inside function” and let it be called \(u\).
- Find the derivative of \(u\), \(\frac{du}{dx}\)
- Find where the expressions you have for \(u\) and \(\frac{du}{dx}\) appear in the integral and replace them in the integrand with \(u\) and \(\frac{du}{dx}\). You may need to first rearrange the equations for \(u\) or \(\frac{du}{dx}\) before substituting. Your integral should have no \(x\)’s anymore after subbing.
- integrate as usual. Don’t forget “+C”
- plug back in your \(u\) formula and call it a day
- (If computing a definite integral, then plug in upper and lower limits in for \(x\), and subtract the results.)
\(\frac{1}{2}e^{(\ln(x)+1)^2}+C\)
