Using Potato Diagrams
Since functions can be thought of as rules that determine what output you get from a given input, we can represent a function simply using an arrow diagram (I like to call them potato diagrams), which consists of two bubbles and arrows pointing from a given function input and to its corresponding output.

We can evaluate the value of a function given a specific input simply by following the arrow from the given input to the output it points to.
For example, with the function given in the potato diagram above, one can evaluate the value of \(f(2)\) by following the arrow from \(2\) in the left potato to the output of the function in the right potato to get \(f(2)=5\).
REMEMBER: Expressions like \(f(2)\) mean “find what comes out of the function if you plug in 2.” This interpretation will be helpful later when we talk about functions defined using means other than potato diagrams. So… burn it into your brain!
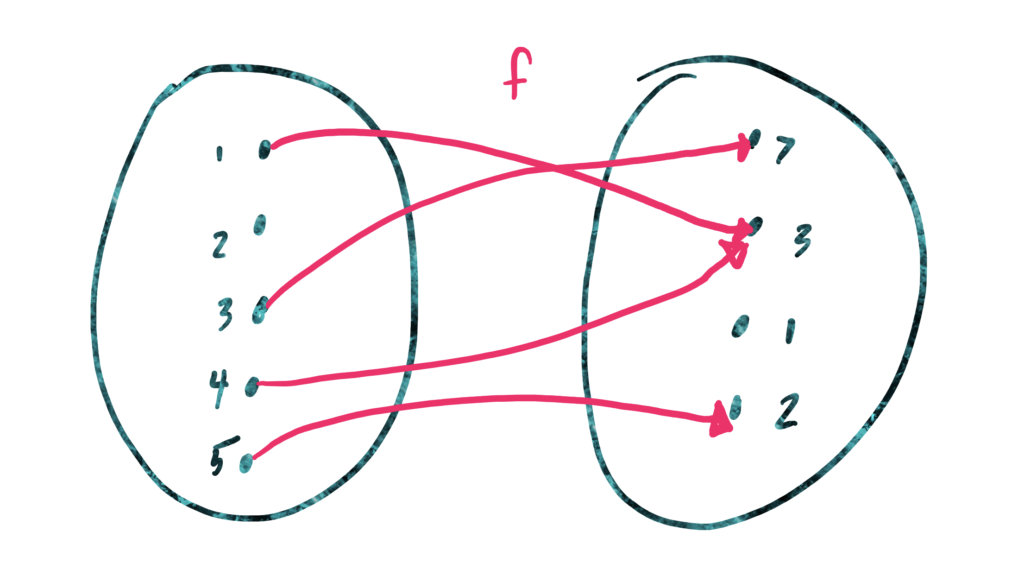
\(f(1)=3\), \(f(3)=7\), and \(f(5)=2\)
Remember that \(f(x)\) means “what is the output of the function on input \(x\)” (where \(x\) is a number). Follow the arrows from \(1, 3\) and \(5\), respectively, in the left potato to their corresponding output in the right potato.

Solution: \(f(2)=4\), \(f(5)=-1\), and \(f(3)=0\).
Remember that \(f(x)\) means “what is the output of the function on input \(x\)” (where \(x\) is a number). Follow the arrows from \(2, 5\) and \(3\), respectively, in the left potato to their corresponding output in the right potato.

Solution: \(\{1,3\}\).
This problem is asking the opposite question, compared to the last two problems. Here, we want to know all possible inputs that give a specific output. So, look for arrows pointing TO \(5\), finding all the elements in the left potato (your possible inputs) that have arrows pointing from them to the number \(5\). Put those inputs in curly brace set notation (because the problem asked for a set).
