The Power Rule for Antiderivatives
The Power Rule for Derivatives… But In Reverse
As indicated in the header, the power rule for antiderivatives is noting more than the power rule for derivatives in reverse! With derivatives, you start by taking the exponent and moving it to the front, and subtract \(1\) from the exponent. With antiderivatives, you start by ADDING \(1\) to the exponent, and then DIVIDE by the (new) exponent; hence the \(n+1\) in the denominator. This similarity is illustrated in the step-diagram below.
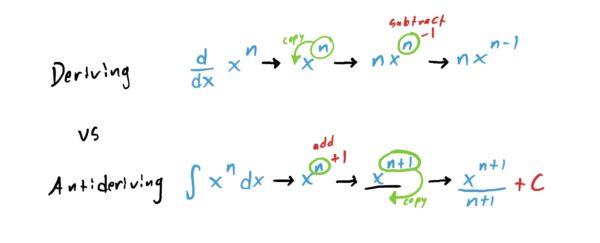
Using the strategy listed above, we start by adding \(1\) to the exponent, giving us an exponent of \(5\), and then divide by that new exponent of \(5\). Whenever we want to find the indefinite integral of a function, we always have to remember to put a “+C” at the end of our final answer to represent the “unknown constant” that was “derived away” to give you the function you started with. All this is shown below in one single step (because it doesn’t need to be more complicated than that).
$$\begin{align} \int x^4\ dx&=\frac{x^5}{5}+C\end{align}$$
A Special Note for Constants and \(f(x)=x\)
We have a neat rule for antideriving things like \(x^2\) or \(x^{25}\) or even \(x^{\frac{2}{3}}\) (yes, the rule works even when you have fractions or decimals as exponents), but what about constant functions like \(f(x)=6\), where the function is just a number? Or how about \(f(x)=x\)?
In either of these cases, it looks like there is “no power” that we can add \(1\) in order to use the power rule. Technically, there IS an implicit power on \(x\) for both of these. Note that if \(a\) is any real number,
$$\begin{align}f(x)&=a\\&=ax^0\end{align}$$
This works because \(x^0=1\). Similarly,
$$\begin{align}f(x)&=x\\&=x^1\end{align}$$
So, now that we can actually “see” the exponents, antideriving these is a piece of cake.
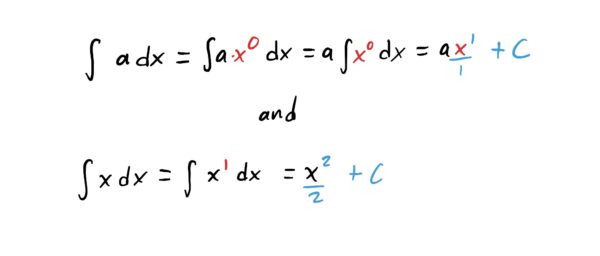
Antideriving Linear Combinations of Functions
Just like with derivatives, antiderivatives can be taken “term-by-term” and “carry along the coefficients.” This is made explicit in the theorem below.
Essentially, what this says is “antiderive each term separately, and bring the constants out in front along for the ride until the end.” Put another way, integrals can be “distributed” and “pass through” constants out in front of functions. How this works is demonstrated in the quick example below.
Using the theorem above, we distribute the integral sign to all three terms, moving the constants out front in order to be multiplied later.
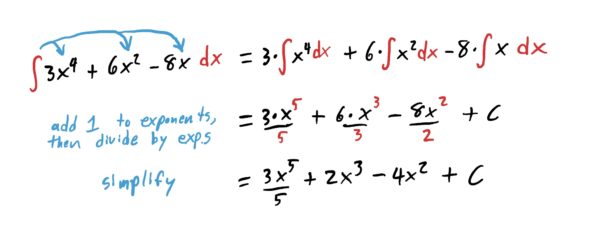
Use the power rule for antiderivatives
For powers of \(x\), add 1 to the exponent, then divide by the new exponent.
Power Rule for Antiderivatives: \(\int x^n\ dx=\frac{x^{n+1}}{n+1}+C\)
\(\int x^2\ dx=\frac{x^3}{3}+C\)
Use the power rule for antiderivatives
For powers of \(x\), add 1 to the exponent, then divide by the new exponent.
Power Rule for Antiderivatives: \(\int x^n\ dx=\frac{x^{n+1}}{n+1}+C\)
\(\int x+1\ dx=\frac{x^2}{2}+x+C\)
Use the power rule for antiderivatives
For powers of \(x\), add 1 to the exponent, then divide by the new exponent.
Power Rule for Antiderivatives: \(\int x^n\ dx=\frac{x^{n+1}}{n+1}+C\)
\(\int 5x^3+4x^2+2\ dx=5\frac{x^4}{4}+4\frac{x^3}{3}+2x+C\)
There is a hidden/invisible number 1 inside that integral
For powers of \(x\), add 1 to the exponent, then divide by the new exponent.
Power Rule for Antiderivatives: \(\int x^n\ dx=\frac{x^{n+1}}{n+1}+C\)
\(\int \ dx=x+C\)
There is a hidden/invisible number 1 inside that integral
For powers of \(x\), add 1 to the exponent, then divide by the new exponent.
Power Rule for Antiderivatives: \(\int x^n\ dx=\frac{x^{n+1}}{n+1}+C\)
\(\int \frac{2x^{\frac{1}{2}}}{3} +x^{\frac{1}{4}}\ dx=\frac{4x^{\frac{3}{2}}}{9}+\frac{4x^{\frac{5}{4}}}{5}+C\)
Power rule for antiderivatives works the same way for fractional exponents
For powers of \(x\), add 1 to the exponent, then divide by the new exponent.
Power Rule for Antiderivatives: \(\int x^n\ dx=\frac{x^{n+1}}{n+1}+C\)
\(\int x^{\frac{1}{2}} -3\sqrt[3]{x}\ dx=\frac{2x^{3}{2}}{3}-\frac{9x^\frac{4}{3}}{4}+C\)
Power rule for antiderivatives works the same way for fractional exponents
For powers of \(x\), add 1 to the exponent, then divide by the new exponent.
Power Rule for Antiderivatives: \(\int x^n\ dx=\frac{x^{n+1}}{n+1}+C\)
\(\int x^{-4} +\sqrt{x}\ dx=-\frac{x^{-3}}{3}+\frac{2x^{\frac{3}{2}}}{3}+C\)
Power rule for antiderivatives works the same way for fractional exponents
For powers of \(x\), add 1 to the exponent, then divide by the new exponent.
Power Rule for Antiderivatives: \(\int x^n\ dx=\frac{x^{n+1}}{n+1}+C\)
\(\int 3x^{-2}-x^{-3}\ dx=-3x^{-1}+\frac{x^{-2}}{2}+C\)
Power rule for antiderivatives works the same way for fractional exponents
For powers of \(x\), add 1 to the exponent, then divide by the new exponent.
Power Rule for Antiderivatives: \(\int x^n\ dx=\frac{x^{n+1}}{n+1}+C\)
\(\int 5x^{-4}+\frac{3}{x^2}\ dx=-\frac{5x^{-3}}{3}-3x^{-1}+C\)
Convert radical to fractional power, then bring all powers of x up to the numerator, making the exponent negative.
For powers of \(x\), add 1 to the exponent, then divide by the new exponent.
Power Rule for Antiderivatives: \(\int x^n\ dx=\frac{x^{n+1}}{n+1}+C\)
\(\int \frac{3}{x^3}+\frac{1}{\sqrt{x}}\ dx=-\frac{3x^{-2}}{2}+2x^{\frac{1}{2}}+C\)
Convert radical to fractional power, then bring all powers of x up to the numerator, making the exponent negative.
For powers of \(x\), add 1 to the exponent, then divide by the new exponent.
Power Rule for Antiderivatives: \(\int x^n\ dx=\frac{x^{n+1}}{n+1}+C\)
\(\int \frac{1}{2\sqrt{x}}-\frac{3}{\sqrt[3]{x}}\ dx=x^{\frac{1}{2}}-\frac{9x^{\frac{2}{3}}}{2}+C\)
FOIL/Expand. Then hit with power rule
For powers of \(x\), add 1 to the exponent, then divide by the new exponent.
Power Rule for Antiderivatives: \(\int x^n\ dx=\frac{x^{n+1}}{n+1}+C\)
\(\int x\cdot(1+x^2)\ dx=\frac{x^2}{2}+\frac{x^4}{4}+C\)
FOIL/Expand. Then hit with power rule
For powers of \(x\), add 1 to the exponent, then divide by the new exponent.
Power Rule for Antiderivatives: \(\int x^n\ dx=\frac{x^{n+1}}{n+1}+C\)
\(\int (x-1)(x+1)\ dx=\frac{x^3}{3}-x+C\)
FOIL/Expand. Then hit with power rule. Of course, you want to convert radicals to fractional powers
For powers of \(x\), add 1 to the exponent, then divide by the new exponent.
Power Rule for Antiderivatives: \(\int x^n\ dx=\frac{x^{n+1}}{n+1}+C\)
\(\int (x-\sqrt{x})(x+\sqrt{x})\ dx=\frac{x^3}{3}-\frac{x^2}{2}+C\)
FOIL/Expand. Then hit with power rule. Of course, you want to convert radicals to fractional powers
For powers of \(x\), add 1 to the exponent, then divide by the new exponent.
Power Rule for Antiderivatives: \(\int x^n\ dx=\frac{x^{n+1}}{n+1}+C\)
\(\int (1+\sqrt{x})^2\ dx=x+\frac{4x^{\frac{3}{2}}}{3}+\frac{x^2}{2}+C\)
Distribute the denominator to each term in the numerator. In other words, break apart the fraction.
For powers of \(x\), add 1 to the exponent, then divide by the new exponent.
Power Rule for Antiderivatives: \(\int x^n\ dx=\frac{x^{n+1}}{n+1}+C\)
\(\int \frac{x-1}{x^3}\ dx=-x^{-1}+\frac{x^{-2}}{2}+C\)
Distribute the denominator to each term in the numerator. In other words, break apart the fraction.
For powers of \(x\), add 1 to the exponent, then divide by the new exponent.
Power Rule for Antiderivatives: \(\int x^n\ dx=\frac{x^{n+1}}{n+1}+C\)
\(\int \frac{2\sqrt{x}+x^2}{x}\ dx=4x^{\frac{1}{2}}+\frac{x^2}{2}+C\)
Distribute the denominator to each term in the numerator. In other words, break apart the fraction.
For powers of \(x\), add 1 to the exponent, then divide by the new exponent.
Power Rule for Antiderivatives: \(\int x^n\ dx=\frac{x^{n+1}}{n+1}+C\)
\(\int \frac{3x^2-\sqrt{x}}{\sqrt{x}}\ dx=\frac{6x^{\frac{5}{2}}}{5}-x+C\)
