$Project Greater Ed Logo$

The Derivative as a Function

Business Calculus The Derivative as a Limit of an Average Rate of Change The Derivative as a Function

The Derivative as a Function

Recall the definition of the ($h$-form of the) derivative at a given $x$-value.

$h$-Form of the Derivative at a Given $x$-Value

Let $f$ be a function defined on an interval $I$ and let $x=c$ be an $x$-value inside this interval. The (first) derivative of $f$ at $x=c$, denoted $f'(c)$, is given by the following:
$$f'(c)=\lim_{h\rightarrow 0} \frac{f(c+h)-f(c)}{h}$$

Now suppose that we want to use this definition of the derivative to find the derivative of the function $f(x)=x^2$ at several different $x$-values, say $x=1,2,3$ and $4$. The process for finding the derivative in each of these four cases is the same; as is the computations required to compute the final answer. This is exhibited in the table below.

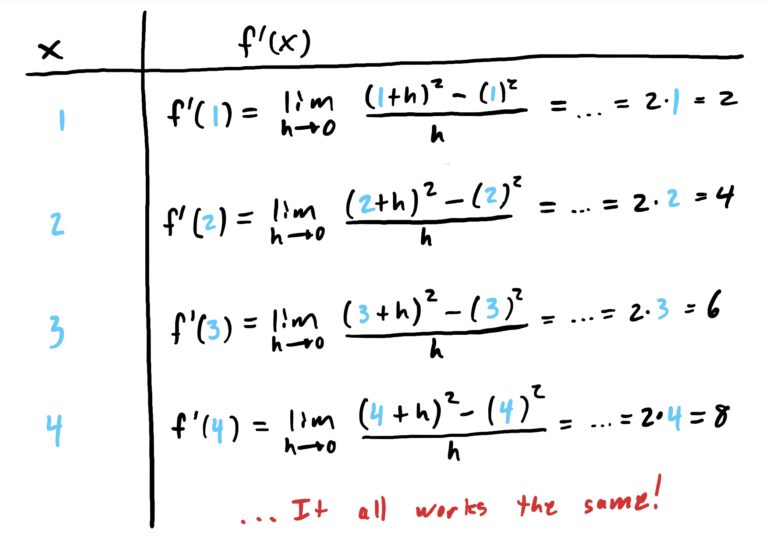
table of derivative results for the function x^2 at the x-values x=1,2,3,4

Since the process of computing this derivative is basically the same, with the only thing that changes being the $x$-values, we could surmise that the process would be the same for any other $x$-value we choose. So, since the process is the same regardless of the $x$-value, why don’t we simply use a “placeholder symbol” for our $x$-value and carry out the process as usual. Let’s call this placeholder (for lack of more appropriate options) “$x$.” Then the derivative at $x$ is computed as:

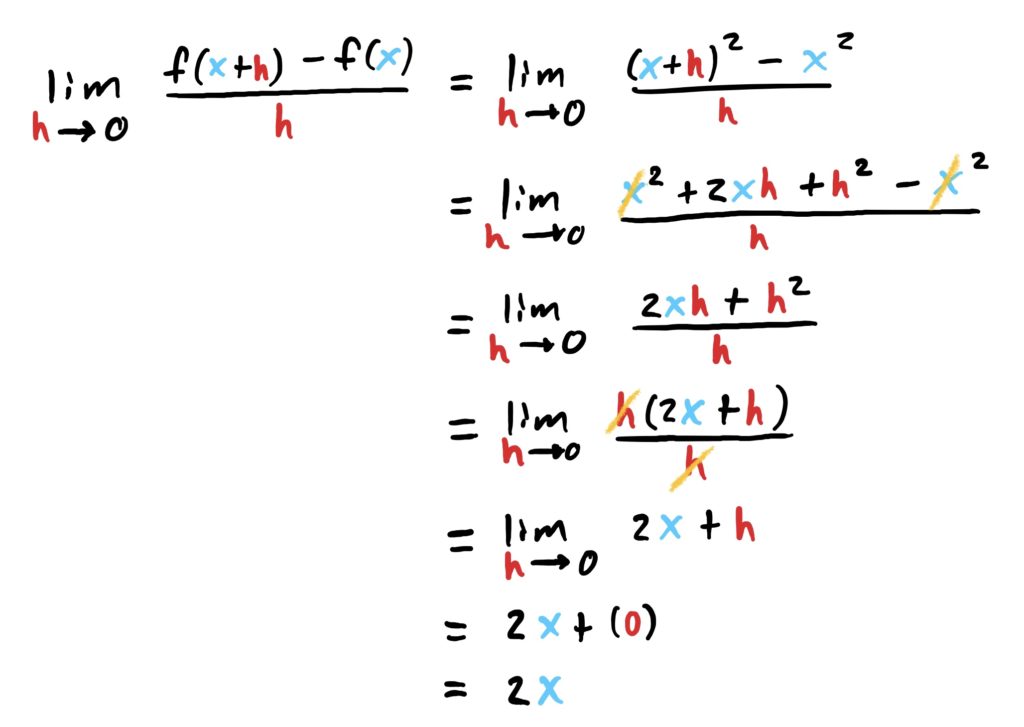
steps for the derivative of x^2 which eventually gives you a result of 2x

Since $x$ was a placeholder for any $x$-value we wanted to find the derivative at, and given that everything above is equal, we essentially have a formula that will tell us the derivative of $f(x)=x^2$ no matter what $x$ is. You can confirm this by plugging $x=1,2,3,4$ into the formula $f'(x)=2x$ and compare with the derivatives in the table we built earlier to see that this formula works.

In general, this idea allows us to build a formula that gives us the slope (or instantaneous rate of change) of a function at any $x$-value we like.

$h$-Form of the Derivative of a Function

Let $f$ be a function defined on an open interval $I$. The (first) derivative of $f$ (on $I$, denoted $f'(x)$, is given by the following:
$$f'(x)=\lim_{h\rightarrow 0} \frac{f(x+h)-f(c)}{h}$$
A function whose derivative exists for every point in $I$ is said to be differentiable (on $I$).

Key Idea

The formula for the derivative of a function $f$ on an open interval $I$ gives you a new function (or, if you prefer, a “formula”) that tells you the slope / instantaneous rate of change of $f$ at any $x$-value on that interval.

Try some of the examples below for finding the derivative of various functions!