Subtracting Binary Numbers
Recall How to Subtract Two Numbers
When we first learned how to subtract multi-digit decimal numbers such as \(7242\) and \(5127\), we learned that if a digit in the first (top) number was less than the digit in the second number written below it (in the subtraction) then we needed to “borrow” a \(1\) from the column to the left of the digits we are trying to subtract. Viz:
In more complicated cases, we need to “chain borrow” across several columns when the next column has a zero (can’t borrow money from someone who has no money… same principle here). This is illustrated in the subtraction of \(10003\) and \(5624\) as below.
We do the exact same thing when subtracting any pair of numbers in any other base. See the following Quick Example for how this works in base 2.
Working from right-to-left, we see that in the rightmost column, we have a pair of \(1\)’s. These can be immediately subtracted, leaving you a result of \(0\).
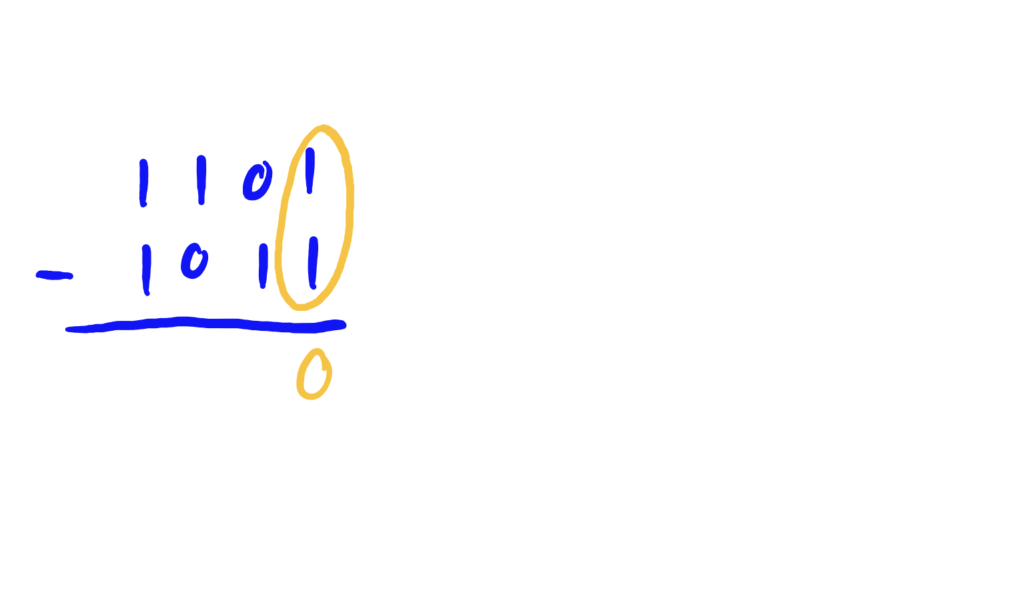
In the column second-from-right, note that we have a \(0\)-digit in the top number and a \(1\)-digit in the bottom number. This means we need to “borrow” a \(1\) from the third-from-right column in order to carry out the subtraction.
In the third-from-right column, we have \(0\)’s in the top and bottom number’s digits, so there is nothing to do here… so we write a zero as the result.
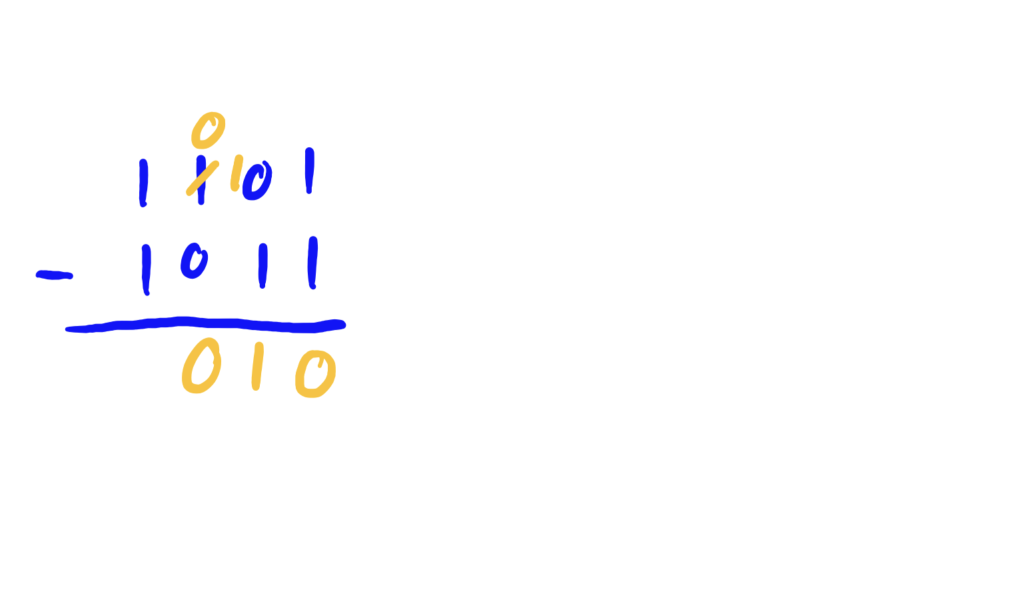
In the last column, we have \(1\)’s in both the top and bottom numbers, so we can subtract these directly, which gives us a final answer.
