$Project Greater Ed Logo$

Set Intersections

Discrete Mathematics Set Operations Set Intersections

Set Intersections

Let $A$ and $B$ be sets. The intersection of the sets $A$ and $B$, denoted $A\cap B$ is the set of all elements that are contained in BOTH $A$ AND $B$.

In other words, the intersection of two sets produces a new set containing what $A$ and $B$ have in common.

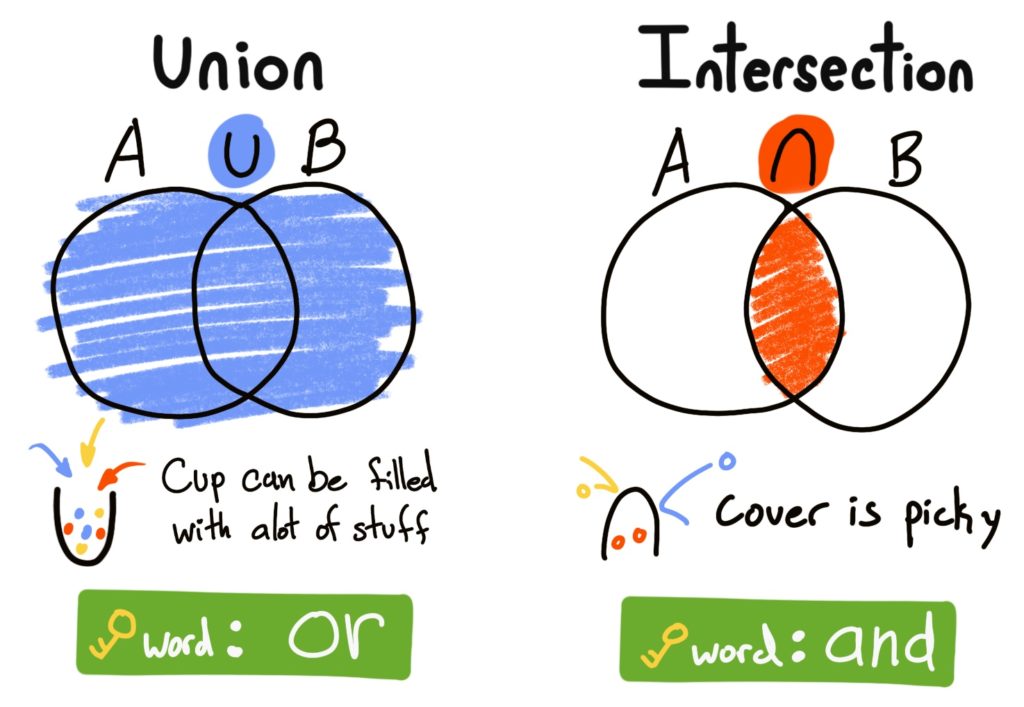
Helpful Mnemonic Devices: Think of the symbol “$\cap$” as the letter “N” in the word “iNtersection” and the symbol “$\cup$” as the letter “U” in the word “Union”. Here’s a visual to help.

$A\cap B=\{3,4,5\}$

The elements 3, 4, and 5 are the only elements that are in BOTH $A$ and $B$. No other element is contained in both sets.

$B\cap C=\{3.14, 5\}$.

Notice that the elements 3.14 and 5 are the ONLY elements that appear in BOTH $B$ and $C$. Thus, they are the only elements in the intersection of the two sets.

$U\cap A=\{1,3,5,7\}=A$

Notice that the elements that are in both sets consist of all the elements in $A$. Hence, the intersection of both sets is simply that; the set $A$.

$B\cap C=\{\}=\emptyset$.

Notice that the two sets have nothing in common. So, the intersection of $B$ and $C$ is empty, which we can represent either as $\{\}$ or $\emptyset$.

$I\cap J=(2,5)$

It is easier to find this result by shading in the interval $I$ and $J$ on a number line and then figuring out where they overlap. As a verbal explanation, $I$ contains all numbers (decimals included) from 0 up to 5 (not including 0 or 5), and $J$ contains all numbers from 2 to 10 (not including 2 or 10), these sets overlap, or intersect, from 2 to 5, but do NOT include either of 2 or 5 since neither 2 nor 5 was included in both $I$ and $J$. See number line below.

$A\cap B=(2,4]$.

The sets $A$ and $B$ have in common all numbers from 2 up to 4 AND including 4 (since $4\in B$). While 2 is contained in $A$, it is NOT contained in $B$, so 2 is NOT in the intersection of the two sets. See number line below.

$J\cap K=\emptyset$.

Notice that $J$ stops at 1, whereas $K$ starts at 4. There is no overlap of these two intervals, and so, they have nothing in common. As always, we designate any set that contains nothing by writing $\emptyset$. (NOTE: we typically don’t write an empty interval, such as $(\ )$for situations like this; just use the empty set notation). The number line for this situation is below.

$I\cap K=[0,3)$.

Notice that the interval $I$ starts at $0$ and includes $0$ and the second interval $J$ ends at $3$. The intervals overlap where indicated in red below.

Previous Topic

Back to Lesson

Next Topic