Product Rule
Deriving Products of Functions
Up until now, we have discussed ways of deriving powers of \(x\), the natural exponential function \(e^x\), and linear combinations of these sorts of functions (i.e. these sorts of functions added or subtracts from one another, perhaps with constant coefficients, such as \(3x^4-2e^x+4\). Now how could we go about deriving products of functions, such as \(x^2\cdot e^x\)? Unfortunately, it is not as easy as just taking the derivative of \(x^2\) and \(e^x\) and multiplying the results. But it’s also not terribly complicated.
In other words, to find the derivative of a product \(f(x)\cdot g(x)\), derive the first function and leave the second alone, then derive the second and leave the first alone, and then add the results. Let’s see this method in action.
Since we have two functions being multiplied, namely \(2x^3\) and \(e^x\), we need to use the product rule. Letting \(f(x)=2x^3\) and \(g(x)=e^x\), the product rule gives us the following result.
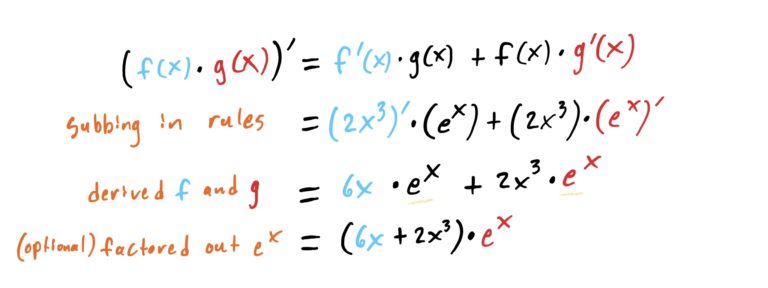
Remember and repeat the following to yourself: “derive the first, leave the second alone, then derive the second, leaving the first alone… then add it all together”
Products of Multiple Functions
What does one do if you have multiple functions being multiplied? How do you derive something like
$$e^x\cdot(x^2+1)\cdot (x^3-2x)\ \ ?$$
It turns out that the rule for deriving a function with several functional factors, such as the above, is very similar to how one handles two functions being multipled.
That is, you derive the first function \(f\) in the first term, leaving the other two alone, derive the second function \(g\) in the second term, leaving the other two alone, and lastly derive the third function \(h\), leaving the other two alone. Then, you add it all together.
Let \(f(x)=e^x\), \(g(x)=x^2+1\) and \(h(x)=x^3-2x\). Then the three-function product rule says
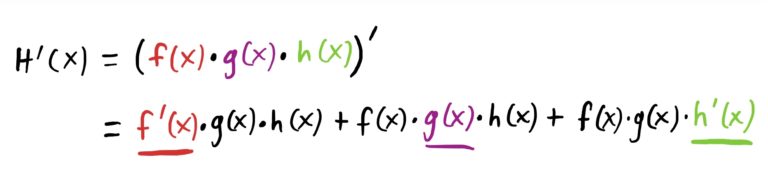
Now, substituting in our \(f\), \(g\), and \(h\), we have
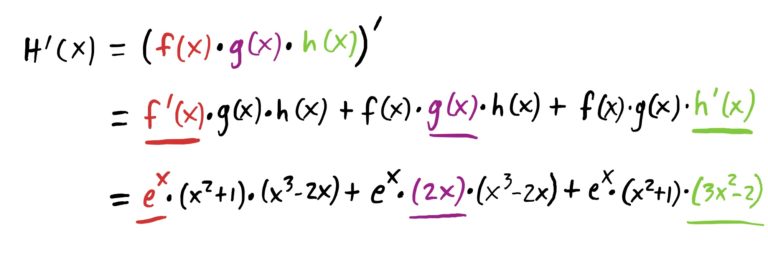
Once you get to this point, you certainly can FOIL/distribute out everything and combine like-terms, or even factor out an \(e^x\), but the problem didn’t ask us to simplify, so we wont. The last line above is the correct derivative, in all of its long-ass glory.
Remember: In the first term, derive the first function. In the second term, derive the second function, in the third term, derive the third function.
This idea above for deriving products can be generalized to four, five, or even more functions being multiplied!
Finding Tangent Lines with the Product Rule
The process of finding tangent lines using doesn’t change. We just have a new way of computing a function’s slope at a given point through use of the product rule. See the example below.
Remember, to find the tangent line at a given point, we need a slope \(m\) at that point and the \(x\) and \(y\)-values at that point as well. Let’s first compute \(m\) by finding the derivative of \(H\) at \(x=1\).
The function \(H\) is the same as the one given in a prior example. We found through the product rule that
$$\begin{align}H'(x)&=(2x^3\cdot e^x)’\\&=(6x+2x^3)\cdot e^x\end{align}$$
If you want to see how this was computed, click the dropdown below.
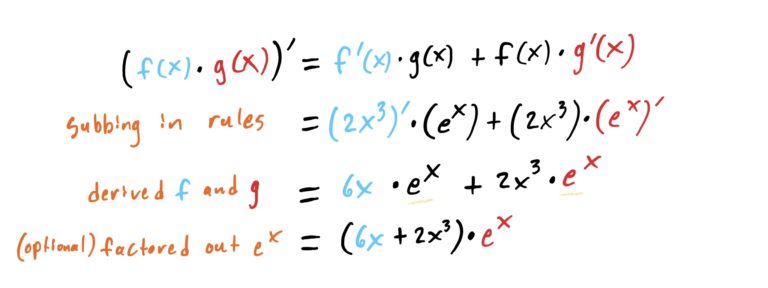
Note that
$$\begin{align}m&=H'(1)\\&=(6(1)+2(1)^3)e^1\\&=8e\\&\approx 21.74624\end{align}$$
Now that we have our slope, we need an \(x\) and \(y\)-value for the point that the function \(H\) and the tangent line have in common. We already are given the \(x\) value. To find the \(y\)-value, simply plug \(x\) into \(H\) (NOT \(H’\)). This gives us:
$$\begin{align} H(1)&=2(1)^3\cdot e^1\\&=2e\\&=5.43656\end{align}$$
In summary, we have \(m=21.74624\), \(x_0=1\), \(y_0=5.43656\). Plug this all into point-slope form \((y-y_0)=m(x-x_0)\). This gives us
$$(y-5.43656)=21.74624(x-1)$$
Solving for \(y\) gives us: \(y=21.74624x-16.30968\). The end!