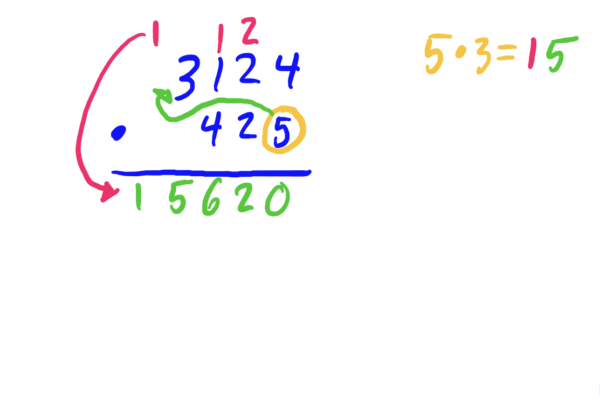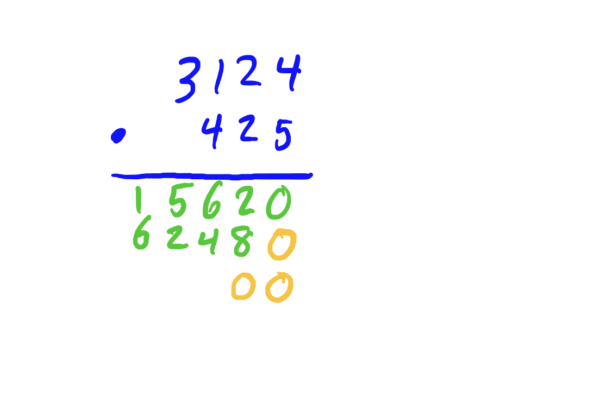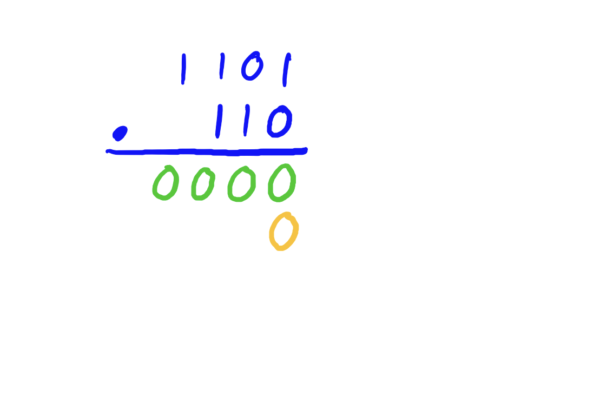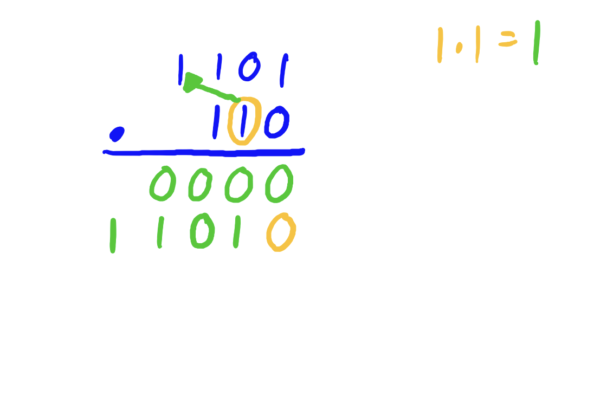Module 1: Basic Set Theory
Set Operations
4 Topics
Module 2: Modular Arithmetic, Divisibility, and the Fundamental Theorem of Arithmetic
Module 3: Functions and Relations
Functions Basics
4 Topics
Module 4: Truth Tables and Symbolic Logic
Truth Tables
2 Topics
Conditional Statements
2 Topics
Module 5: Basic Direct Proofs
Basic Direct Proofs
3 Topics
Module 6: Proof Techniques Part 1: Contrapositive and Contradiction
Module 7: Sequences, Sums, and Products
Module 8: Proof Techniques Part 2: (Weak) Induction
Module 9: Recurrence Relations and Recursion
Module 10: Counting Systems (Binary, Hex, Octal, etc.)
Arithmetic in Binary
4 Topics
Module 11: Combinatorics
Module 12: Graph Theory
Paths and Circuits
2 Topics
Module 13: Review
Multiplying Binary Numbers
Multiplying Numbers without Calculators…
Recall that when you first learned to multiply two multi-digit numbers such as \(3124\cdot 425\), you probably used the following procedure:
Step 1: Multiply each digit of the top number by the \(1\)’s digit of the bottom number, keeping the \(1\)’s digit, and carrying the \(10\)’s digit
Step 2: Write a zero below the \(1\)’s digit of what you got in the last step, then repeat step 1, but with the \(10\)’s digit of the second number. Be sure to add the number that got carried in the last step to your answer here.
Step 3: Write a pair of zeros under the \(1\)’s digit and \(10\)’s digit of the last line, and repeat step 1 with the \(100\)’s digit of the second number. Be sure to add any carried numbers to your answer.
Step 4: Add up all three lines to get the final answer.
How Multiplication Works in Base 2
It turns out that multiplication of numbers works exactly the same way in binary, except with the added benefit that you won’t ever need to carry a digit to the next location. In other bases, carrying will be required when the product of the digits you’re multiplying give you a product that is bigger than the base. Perhaps more on this later.

Step 1: Multiply each digit of the top number by the \(1\)’s digit of the bottom number
Step 2: Write one zero below the \(1\)’s digit of your answer to step 1, then multiply each digit in the top number by the \(10\)’s digit in the bottom number.
Step 3: Write two zeros below the \(1\)’s and \(10\)’s digit of your answer, then multiply each digit in the top number by the \(100\)’s digit in the bottom number.
Step 4: Since we have used all digits in the bottom number, we now add up the results IN BASE 2. The final answer is the result of this addition.
\(11110_2\)
\(1101001_2\)
\(111111_2\)