$Project Greater Ed Logo$

Modulo Operator

Discrete Mathematics Modular Arithmetic Modulo Operator

Imagine you are staring at an analog clock face with the usual 12 ticks representing “hours.” If you start with the hours hand at $12$, where would you be on your clock if you added $17$ hours (i.e. $17$ hours elapsed) if you moved around the clock, well… clockwise?

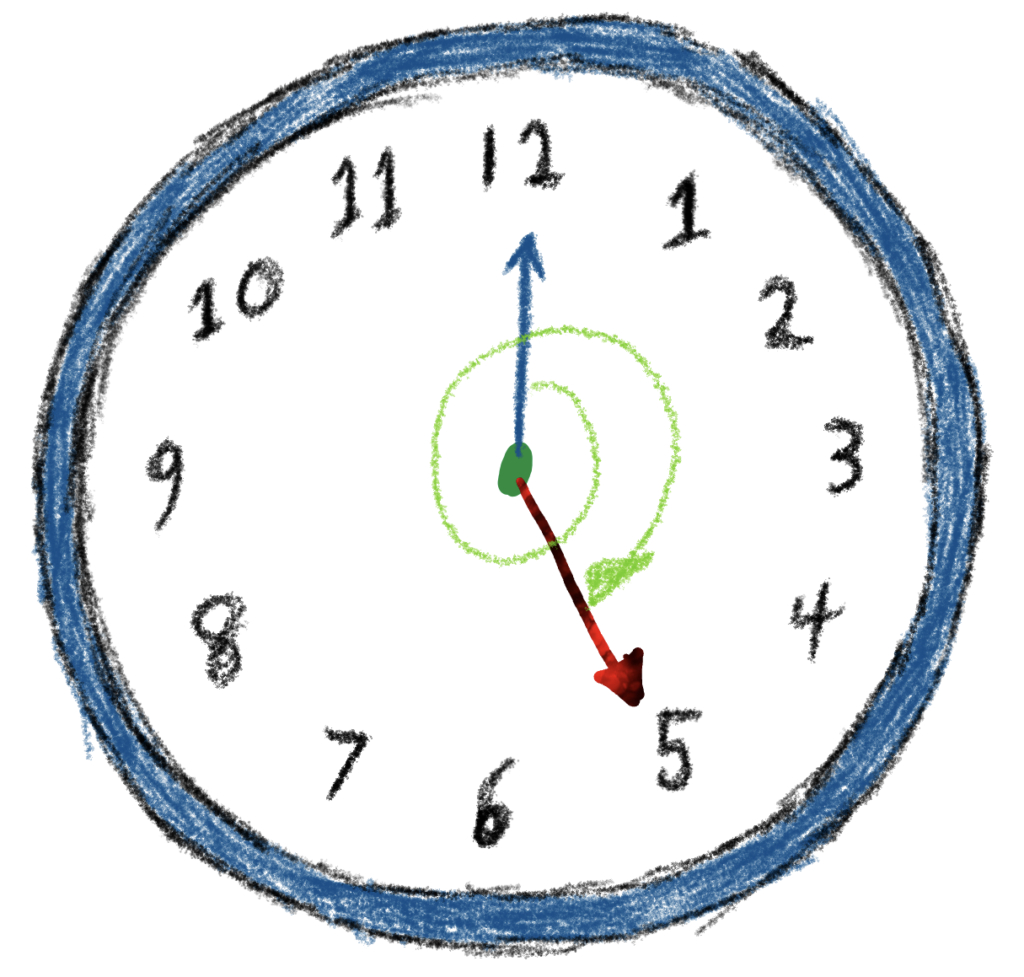
Answer: $5$-o’clock, because, as you count off $17$ hours working around the clock, well… clockwise, you will cross through your starting point at hour $12$ and then add $5$ more hours.

Now, lets change up the clock a bit so that the starting point is $0$ instead of $12$, representing that we have not counted off any hours at the start. Where on the clock would you be if you added $25$ hours?

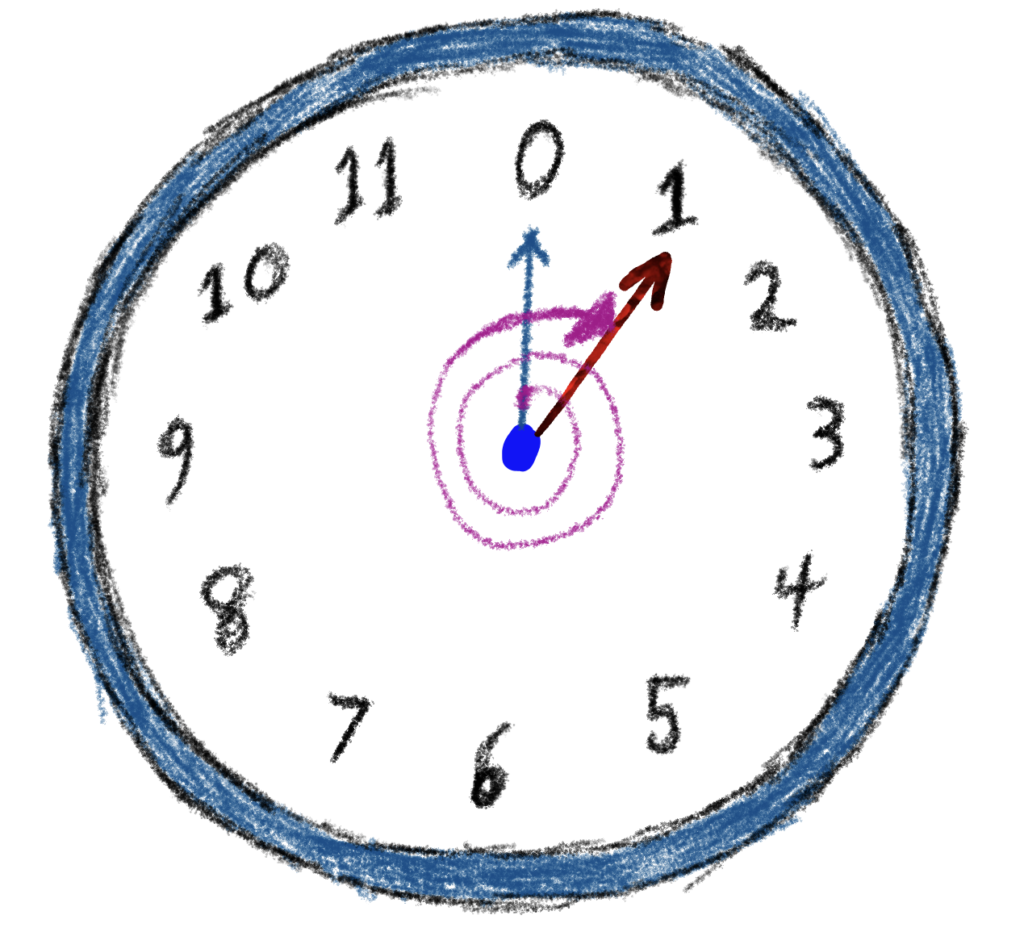
Answer: $1$-o’clock, because you’d loop around your clock twice for the first $24$ hours, landing where you started at $0$, and then adding $1$-more hour gets you to $1$-o’clock, so that the full $25$ hours has elapsed.

One more. Suppose you have instead a $6$-hour clock (as opposed to the usual $12$), and we start counting at the top of the clock, designated by a $0$. Where would you be on the clock after $23$ “hours” elapsed?

Answer: $5$-“o’clock,” because you’d loop around your clock $3$ times after 18 “hours” elapsed, landing where you started, and then adding $5$ more “hours” to get the full $23.$

If you think carefully about what was done in the last three examples, to determine where we ended up on the clock, we first divided up the number given (like $23$, for instance, in the $6$-hour clock example) by the number of hours on the clock to determine how many times we’d loop completely around the clock. Then, we added on the hours that remained to determine where we’d finally end up on the clock.

Therefore, because of this looping around the clock, all that really mattered for determining where we’d end up on the clock was the remainder that we’d get if we divided our given number of hours by the number of hours on our clock. In the last example’s case, the remainder of $23$ divided by $6$ is $5$, and so we ended up at $5$-o’clock.

This idea of “clockwork math” is quite common in many areas of math, so we formalize here in the next definition.

Modulo Operator

Let $n$ and $m$ be integers. We define the expression $n\ mod\ m$ to be the positive remainder one gets when $n$ is divided by $m$.

Note

The remainder obtained in the definition above is the same as the remainder obtained the Quotient-Remainder Theorem equation $n=mq+r$, where $0\leq r <m$. So, the remainder you get needs to be positive and less than the divisor $m$.

Key Idea

When computing $n\ mod\ m$:
If $n$ is positive, repeatedly subtract $m$ from $n$ until you get the smallest positive number possible. That number is the answer, and is the result of finding the remainder that you’d get if you divided $n$ by $m$.

If $n$ is negative, repeatedly add $m$ to itself until you get a positive number. That number is your answer and is the result of finding the positive remainder that you’d get if you divided $n$ by $m$.

To illustrate the key idea above with an example, suppose we want to compute $30\ mod\ 4$. Subtracting $4$ as many times as we can from $30$ without “going negative” (The subtraction pattern is $30, 26,22,18,14,10,6,2$) gives us $2$, i.e. the smallest possible positive number resulting from this repeated subtraction. Equivalently, $2$ is the remainder one would get when attempting to divide $30$ by $4$.

$5\ mod\ 2=1$.

$2$ evenly divides $5$ twice, leaving a remainder of $1$ and the remainder is what we want.

Subtracting $2$ from $5$ as many times as possible without “going negative” gives $1$.

$12\ mod\ 5=2$.

$5$ evenly divides $12$ twice, leaving a remainder of $2$ and the remainder is what we want.

Subtracting $5$ from $12$ as many times as possible without “going negative” gives a result of $2$ as well.

$121\ mod\ 11=0$

$11$ evenly divides $121$ eleven times, leaving a remainder of $0$ and the remainder is what we want. Don’t always need to have a remainder.

$120\ mod\ 7=1$.

$7$ divides $120$ evenly 17 times, leaving a remainder of $1$.

Subtracting $7$ from $120$ repeatedly gives us $120,113,106,99,92,85,78,71,64,57, 50, 43, 36, 29,22,15,8,1, -6$. The last positive number in this list is the division remainder we are after.

$-15\ mod\ 4=1$

Since the dividend $-15$ is negative, and we want a positive remainder, we need to “overshoot” in our division so that after dividing we have to add something smaller than $4$ back to get $-15$. Notice that $4\cdot(-4)+1=-16+1=-15$. This positive “remainder” of $1$ is exactly what we are after.

Alternatively, add $4$ to $-15$ as many times as you can until you get a positive number. When you do this, you will get the list $-15,-11,-7,-3,1$. The $1$ is the answer we are after.

$-123\ mod\ 25=2$

Since the dividend $-123$ is negative, and we want a positive remainder, we need to “overshoot” in our division so that after dividing we have to add something smaller than $25$ back to get $-123$. Notice that $25\cdot(-5)+2=-125+2=-123$. This positive “remainder” of $2$ is exactly what we are after.

Alternatively, add $25$ to $-123$ as many times as you can until you get a positive number. When you do this, you will get the list $-123, -98, -73, -48, -23,2$. The $2$ is the answer we are after.

$-101\ mod\ 15=4$

Since the dividend $-101$ is negative, and we want a positive remainder, we need to “overshoot” in our division so that after dividing we have to add something smaller than $15$ back to get $-101$. Notice that $15\cdot(-7)+4=-105+4=-101$. This positive “remainder” of $4$ is exactly what we are after.

Alternatively, add $15$ to $-101$ as many times as you can until you get a positive number. When you do this, you will get the list $-101, -86, -71, -56, -41, -26, -11, 4$. The $4$ is the answer we are after.

Previous Lesson

Back to Lesson

Next Topic