$Project Greater Ed Logo$

Injections, Surjections, and Bijections

Discrete Mathematics Functions Basics Injections, Surjections, and Bijections

In this topic, we classify functions as injective, surjective, bijective, or neither. Each of these classifications can be used to describe how two sets (i.e. the domain and codomain of the given function) are related to one another.

Injective/One-to-One Function

Let $f:A\rightarrow B$ be a function. We say that $f$ is an injection (or say “$f$ is injective” or “$f$ is one-to-one”) if for all $a,b\in A$ $f(a)=f(b)$ implies $a=b$.

Put another way, a function $f$ is injective/one-to-one if different inputs give you different outputs. A function $f$ is NOT injective/one-to-one if different inputs give you the same output. Put another way, a function is NOT one-to-one/injective if there are duplicate outputs.

Surjective/Onto Function

Let $f:A\rightarrow B$ be a function. We say that $f$ is a surjection (or say “$f$ is surjective,” or “$f$ is onto” if for every $b\in B$ there is an $a\in A$ such that $f(a)=b$.

In other words, a function $f$ is surjective if it “hits” every element in the codomain. Put another way, $f$ is surjective if the range of $f$ is equal to the codomain (the function misses no possible output).

When a function is both injective and surjective, it gets a special designation.

Bijective Function

A function $f:A\rightarrow B$ is said to be bijective (or a bijection) if it is both injective and surjective.

Another name for a bijection is one-to-one correspondence.

Essentially, a bijection is a function that uniquely pairs each element of the domain with an element in the codomain, and vice-versa. Each element of the domain is paired with a unique element of the codomain, and each element of the codomain is paired with a unique element of the domain. In other words, $f$ attains all possible outputs (it misses nothing) and there are no duplicate outputs.

$f$ is injective, but not surjective (so therefore not bijective)

Notice that there are no duplicate outputs for our function, so each element in the domain is uniquely paired with an element of the codomain. However, the function is NOT surjective because there are elements of the codomain that are not “hit” by the function; that is, using the definition of surjectivity, there is at least one element of the codomain that such that no element of the domain maps to it.

Surjective, but not injective.

The function is not injective because it has duplicate outputs. Using the definition of injectivity, there are two different inputs (such as $1$ and $3$) that have the same output.

The function is surjective because every element of the codomain is “hit” by the function. That is, for all $y\in B$ there is an element $a\in A$ such that $f(a)=y$.

Since the function is only surjective, it cannot be bijective.

Neither injective nor surjective.

Note that both $1$ and $2$ map to $1$ (i.e. they have the same $y$-value. So therefore $f$ is not injective.

Note also that the codomain is $\{1,2,3,4,5\}$ and the only $y$-values that we get out of our function are $1,3,4,5$, but not $2$.

Neither!

Note that the function is not injective because there are duplicate $y$-values (i.e. outputs). To support this, if you plug in $x=-1$ and $x=1$ you will get the same $y$-value.

Note also that the function is not surjective because there are certain $y$-values that are never “hit” by the function. To support this, we first note that the codomain of the function is implicitly the set of all real numbers $\mathbb{R}$, and secondly note that there is no input $x$-value that gives us a $y$-value of $y=-1$. Put another way, the range of the function is not the same as the codomain.

Bijective!

The function is injective because there are no duplicate $y$-values. Put another way, there are no two $x$-values that you can plug in and get the same $y$-value out for. Every $x$-value is associated with a unique $y$-value.

Also, the function is onto because there is no $y$-value that is “missed” by the function. That is, for any real number $y$-value $b$ you can think of, there is an $x$ value $a$ that can be plugged into the function so that $f(a)=b$.

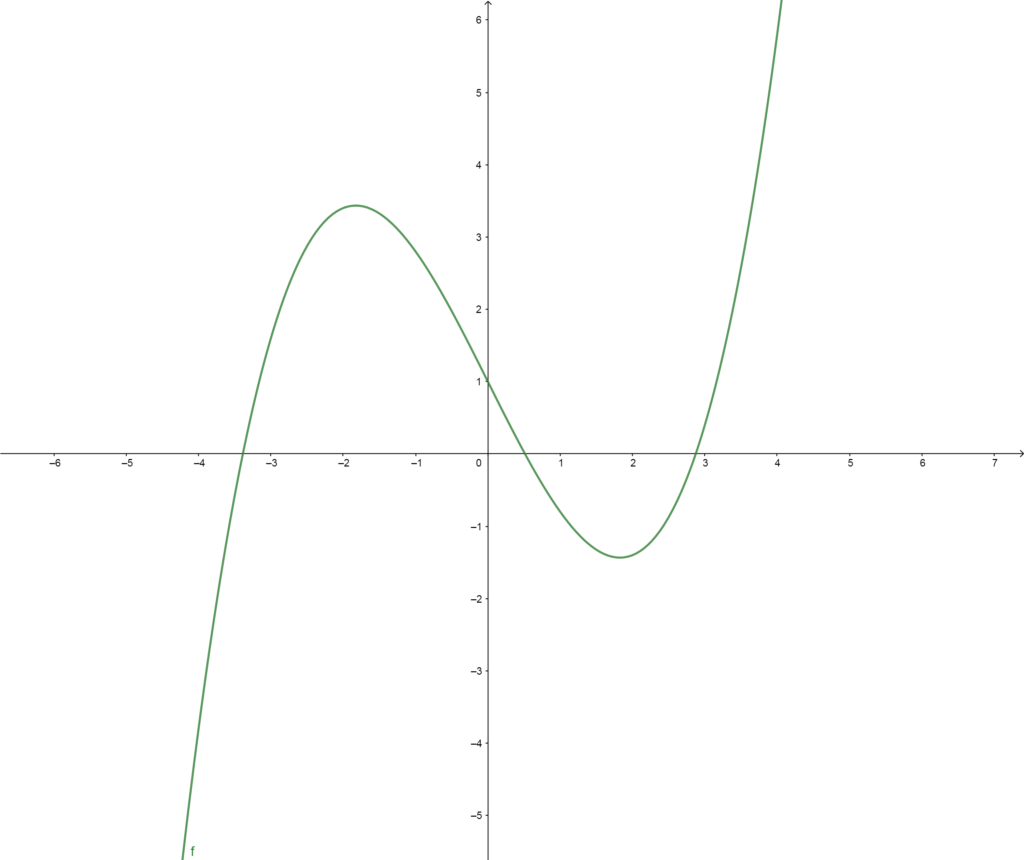
Surjective, but not injective.

The function is NOT injective because there are duplicate outputs. Note that the function’s graph crosses the $x$-axis three times, so there are three $x$-values for which we get the output $y$-value $y=0$.

We can conclude that $|B|=5$ as well!

Since $f$ is bijective, it is one-to-one and onto. Therefore, every input is mapped to a unique output, with no repeated outputs. Furthermore (by surjectivity), every output has a corresponding input, so no element in the codomain is missed.

In other words, there are five arrows coming out of the five elements of $A$, all going to different places so that no element in the codomain is omitted. This implies that the order of $A$ and $B$ must be the same.

Previous Topic

Back to Lesson

Next Lesson