$Project Greater Ed Logo$

Initial Value Problems: Solving for C

Business Calculus Antiderivatives and Basic Rules for Such Initial Value Problems: Solving for C

Recall where the “+C” came from

Let $y(x)$ be a function and suppose we are given it’s derivative $y'(x)=3x^2$. If our goal is to use this information to find the original function $y$ from it’s derivative, we note that the power rule for antiderivatives gives us an antiderivative $x^3$. While it is certainly true that $\frac{d}{dx} x^3 = y'(x)$ (i.e. $x^3$ ‘s derivative matches the one we were given) it is NOT the only function with this derivative! Notice that the functions $x^3+1$, $x^3+5000$, $x^3-5.124$ and $x^3+412384182$ all have the same derivative of $3x^2$, making each of these (and infinitely many others) a perfectly valid answer for what $y(x)$ could be.

Notice also that the difference between all these candidate answers for $y(x)$ is the constant we are adding or subtracting to/from the $x^3$. All of these different constants would vanish when you derive any of these candidates, giving you $y'(x)=3x^2$.

Thus, if we simply started with the derivative $y'(x)=3x^2$ and we want to find the original function $y(x)$ whose derivative is $y'(x)=3x^2$, we would write $y(x)=x^3+C$ where the $+C$ represents the constant that would get derived away when going from $y$ to $y’$. Because that constant got “derived away,” there is not enough information to determine what that constant was originally.

Sometimes, we are given enough information that would help us determine what C is.

Finding the Constant C

Suppose, again, that we are given a function’s derivative $y'(x)=3x^2$ and we are again tasked with determining the antiderivative $y(x)$ of $y'(x)$ given also a little extra information: $y(1)=4$ (i.e. we know a single point that the graph of $y$ passes through).

In the last section we said that there are many possible antiderivatives for $y'(x)=3x^2$, all of which differ by a constant $C$. Specifically, we said that the original function $y$ must have the form $y(x)=x^3+C$ where $C$ is an unknown constant.

Recall from a precalculus or algebra course that when you add or subtract a constant $C$ to/from a function this has the effect of shifting the function’s graph up or down by $C$. Because of this, our solution for $y(x)$ can be any of the following graphed functions (which are all shifted up or down based on what $C$ is).

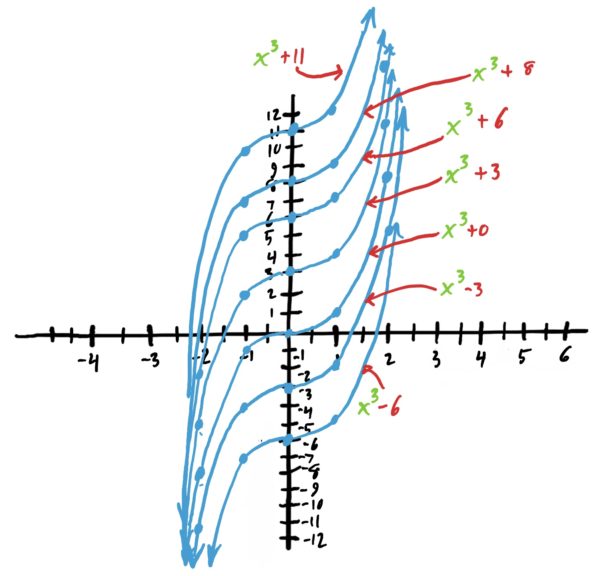
x^3+c for various values of C graphed out

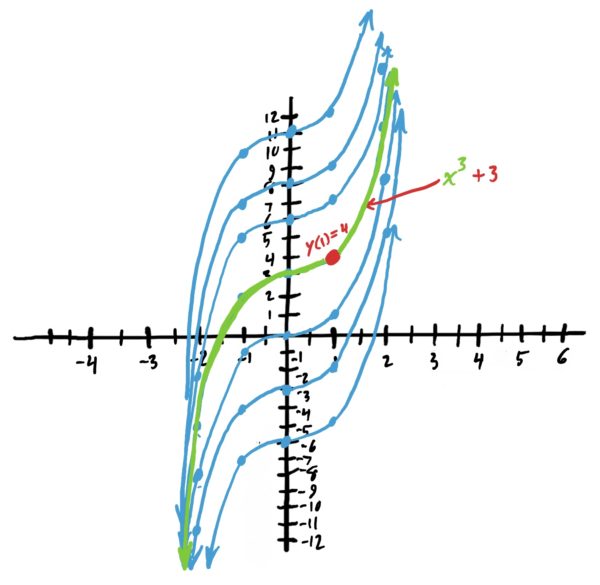
So, if we know that $y(1)=4$, which of these graphs is the function we want for $y(x)$? Since $y(x)=x^3+C$ for some $C$, and $y(1)=4$ we know that $(1)^3+C=4$ (when we plug in $x=1$ and set it equal to $y=4$). Solving for $C$ gives us $C=3$. Therefore, our antiderivative of $y'(x)=3x^2$ given that $y(1)=4$ is $y(x)=x^3+3$. The correct antiderivative graph is highlighted below. Note that the condition of $y(1)=4$ essentially told us which one we wanted (and therefore what $C$ is).

Solving Initial Value Problems (i.e. Solving for $C$)

Suppose you are given a function’s derivative $f'(x)$ (perhaps written as $\frac{dy}{dx}$) and are asked to find the original function $f(x)$ given initial value information $f(x_0)=y_0$ where $x_0$ and $y_0$ are real numbers. The steps are:

1.) Find the indefinite integral of $f'(x)$, $\int f'(x)\ dx$: That is, find an antiderivative of $f'(x)$ using whatever rules for antiderivatives you need, including a $+C$ at the end to represent the unknown constant.

2.) Plug $x_0$ into your result, and set it equal to $y_0$

3.) Solve for $C$ and plug it in for the $C$ in step 1.

We start by finding the indefinite integral $\int 2x+1\ dx$. This is

$$y(x)=\int 2x+1\ dx = x^2+x+C$$

for some unknown $C$ that we will solve for next.

We are given that $y(0)=5$. So this implies

$$(0)^2+(0)+C=5$$

But this immediately gives us that $C=5$. Therefore the antiderivative of $\frac{dy}{dx}=2x+1$ where $y(0)=5$ is

$$y(x)=x^2+x+5$$

Solving up from second (or more) derivatives

Suppose you are given a function’s second derivative $y”(x)=5x$ and an initial condition for the derivative $y'(x)$ and the original function $y(x)$, specifically $y'(0)=1$ and $y(0)=3$. To go from teh second derivative given all the way up to the original function, simply rinse-and-repeat the steps above! You’ll end up antideriving twice and solving for an unknown constant twice. This is illustrated in the mini example below.

Start by finding the antiderivative of $y”(x)=5x$. This will give us a general form for the first derivative $y'(x)$.

$$y'(x)=\int 5x\ dx=\frac{5x^2}{2}+C$$

Before antideriving again to get $y(x)$ we need to first find $C$. Plug in the initial value information $y'(0)=1$. This gives us that

$$\frac{5(0)^2}{2}+C=1$$

which implies (after simplifying) that $C=1$. Therefore, $y'(x)=\frac{5x^2}{2}+1$.

Now we want to find $y(x)$, so we repeat the process above.

$$\int \frac{5x^2}{2}+1\ dx=\frac{5x^3}{6}+x+C$$

Since we know that $y(0)=3$, the above implies

$$\frac{5(0)^3}{6}+(0)+C=3$$

Which implies $C=3$. Therefore, we have the final answer for $y(x)$:

$$y(x)=\frac{5x^3}{6}+x+3$$

First find the antiderivative of the function given, then plug in the given x-value 0, and set the result equal to 1. Solve for C.

Power Rule for Antiderivatives: $\int x^n\ dx=\frac{x^{n+1}}{n+1}+C$