$Project Greater Ed Logo$

How the Method Works

Business Calculus The U-Substitution Method How the Method Works

Recall the Chain Rule for Derivatives

Suppose you have a function like $f(x)=(x^3+1)^5$ and you want to find $f'(x)$. We would use the chain rule, which tells us to first derive the “outside function” $(—-)^5$, leave the inside alone, and then multiply by the derivative of the inside function. This gives you $f'(x)= 5\cdot (x^3+1)^4\cdot 3x^2 = 15x^2\cdot (x^3+1)^4$.

Now, what if instead we were given the function $f(x)=15x^2\cdot (x^3+1)^4$ and we are asked to antiderive it? Noting that antideriving is just “backwards deriving,” I can put on my Sherlock Holmes hat and observe that the chain rule was probably used to get the derivative $f(x)=15x^2\cdot (x^3+1)^4$ because the derivative of the inside is $3x^2$ which is close to what we have on the outside. So, in order to antiderive this, if I could somehow work backwards by removing the derivative of the inside function from that $15x^2$ on the outside and then antiderive the outside $(—-)^5$, that would give me an antiderivative of $f(x)$. This idea is entirely encapsulated in the idea of U-Substitution given explicitly below.

(The Basic) U-Substitution Method for Antideriving

Suppose you are given a function of the form $h(x)=f(g(x))\cdot g'(x)$ and your goal is to find the indefinite integral of $h$, $\int f(g(x))\cdot g'(x)\ dx$. The steps are as follows:
1. Identify the inside function and let it be called $u$ (so $u=g(x)$).

2. Derive $u$ to get $\frac{du}{dx}$. That is $\frac{du}{dx}=g'(x)$

3. Replace your $g(x)$ and $g'(x)$ functions in the integrand with your $u$ and $\frac{du}{dx}$ respectively, and “cancel the $dx$” in the denominator of $\frac{du}{dx}$ with the differential $dx$ at the end of the integral so there are no more $x$’s anywhere.

4. Antiderive as usual using whatever rules are needed.

5. Replace any remaining $u$’s in your result with $g(x)$.

First we identify the inside function and call it $u$:

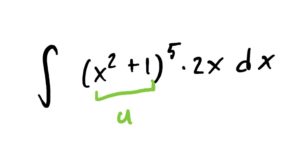
Then we derive our $u=x^2+1$ to get $\frac{du}{dx}=2x$. Now, every place we see $x^2+1$ we will replace it with a $u$ and every place we see $2x$ we will replace it with $\frac{du}{dx}$, and then “cancel” the $dx$’s.

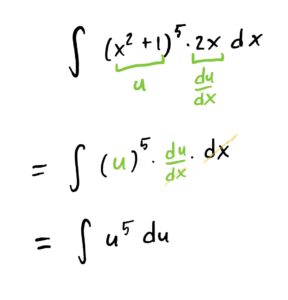
Now that we have no $x$’s in the integrand and only have $u$’s, we will antiderive the current integrand in terms of $u$ as usual:

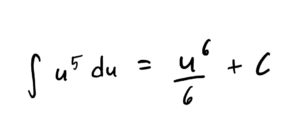
Lastly, we replace all $u$’s with $x^2+1$ to get the final answer (because the original problem was in terms of $x$, not these $u$’s that we substituted to help with the problem).

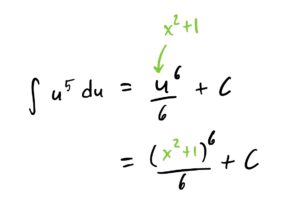
Making alterations to the $\frac{du}{dx}$ Equation

Suppose we want to find $\int (x^5+3)^6\cdot x^4\ dx$. Now if we let $u=x^5+3$, then $\frac{du}{dx}=5x^4$ which is NOT EXACTLY what we have being multiplied on the outside. As such, we cannot carry out the substitution just yet because of this mismatch. We need to make a few alterations to the $\frac{du}{dx}$ equation before we can substitute. This is illustrated in the quick example below.

Let $u=x^5+3$. Then note that $\frac{du}{dx}=5x^4$. Since we have $x^4$ in the integrand, we will get $x^4$ by itself on one side of the equation $\frac{du}{dx}=5x^4$ so we have something to replace the $x^4$ with. Thus, we have:

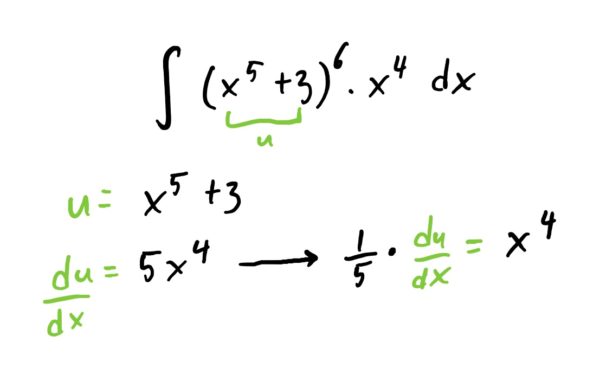
rearranging the du/dx equation to get the x^4 by itself

Now we can replace $x^5+3$ with $u$ and $x^4$ with $\frac{1}{5}\cdot \frac{du}{dx}$ respectively. This gives us

Now we can antiderive as usual in terms of $u$, bringing the $\frac{1}{5}$ along for the ride.

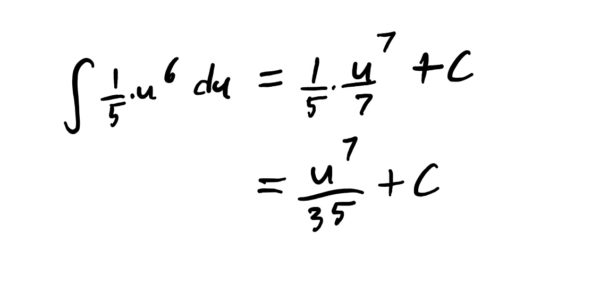
Lastly, we replace the $u$ with the original $x^5+3$ and call it a day:

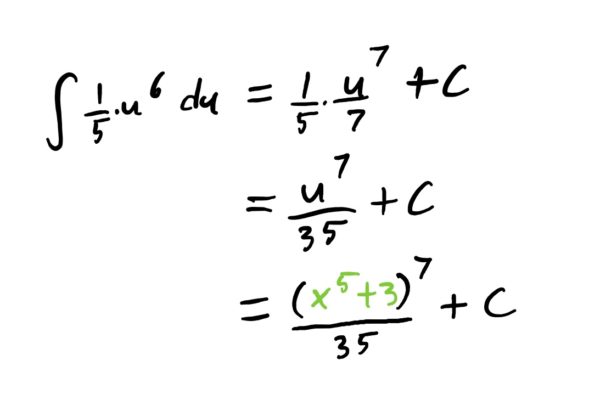
Compute the following antiderivatives

Let $u=x^3+1$

First find an “inside function” and let it be called $u$.
Find the derivative of $u$, $\frac{du}{dx}$
Find where the expressions you have for $u$ and $\frac{du}{dx}$ appear in the integral and replace them in the integrand with $u$ and $\frac{du}{dx}$. You may need to first rearrange the equations for $u$ or $\frac{du}{dx}$ before substituting. Your integral should have no $x$’s anymore after subbing.
integrate as usual. Don’t forget “+C”
plug back in your $u$ formula and call it a day
(If computing a definite integral, then plug in upper and lower limits in for $x$, and subtract the results.)

$\frac{(x^3+1)^{21}}{21}+C$

Let $u=2x+1$

First find an “inside function” and let it be called $u$.
Find the derivative of $u$, $\frac{du}{dx}$
Find where the expressions you have for $u$ and $\frac{du}{dx}$ appear in the integral and replace them in the integrand with $u$ and $\frac{du}{dx}$. You may need to first rearrange the equations for $u$ or $\frac{du}{dx}$ before substituting. Your integral should have no $x$’s anymore after subbing.
integrate as usual. Don’t forget “+C”
plug back in your $u$ formula and call it a day
(If computing a definite integral, then plug in upper and lower limits in for $x$, and subtract the results.)

$\frac{(2x+1)^{301}}{602}+C$

Let $u=3x+5$

First find an “inside function” and let it be called $u$.
Find the derivative of $u$, $\frac{du}{dx}$
Find where the expressions you have for $u$ and $\frac{du}{dx}$ appear in the integral and replace them in the integrand with $u$ and $\frac{du}{dx}$. You may need to first rearrange the equations for $u$ or $\frac{du}{dx}$ before substituting. Your integral should have no $x$’s anymore after subbing.
integrate as usual. Don’t forget “+C”
plug back in your $u$ formula and call it a day
(If computing a definite integral, then plug in upper and lower limits in for $x$, and subtract the results.)

$\frac{(3x+5)^{3.5}}{10.5}+C$

Let $u=x^2+x$. Also, convert radical to fractional power.

First find an “inside function” and let it be called $u$.
Find the derivative of $u$, $\frac{du}{dx}$
Find where the expressions you have for $u$ and $\frac{du}{dx}$ appear in the integral and replace them in the integrand with $u$ and $\frac{du}{dx}$. You may need to first rearrange the equations for $u$ or $\frac{du}{dx}$ before substituting. Your integral should have no $x$’s anymore after subbing.
integrate as usual. Don’t forget “+C”
plug back in your $u$ formula and call it a day
(If computing a definite integral, then plug in upper and lower limits in for $x$, and subtract the results.)

$\frac{4(x^2+x)^{\frac{3}{2}}}{3}+C$

Let $u=x^2+4$

First find an “inside function” and let it be called $u$.
Find the derivative of $u$, $\frac{du}{dx}$
Find where the expressions you have for $u$ and $\frac{du}{dx}$ appear in the integral and replace them in the integrand with $u$ and $\frac{du}{dx}$. You may need to first rearrange the equations for $u$ or $\frac{du}{dx}$ before substituting. Your integral should have no $x$’s anymore after subbing.
integrate as usual. Don’t forget “+C”
plug back in your $u$ formula and call it a day
(If computing a definite integral, then plug in upper and lower limits in for $x$, and subtract the results.)

$\frac{-(x^2+4)^{-3}}{6}+C$

Let $u=x-20$

First find an “inside function” and let it be called $u$.
Find the derivative of $u$, $\frac{du}{dx}$
Find where the expressions you have for $u$ and $\frac{du}{dx}$ appear in the integral and replace them in the integrand with $u$ and $\frac{du}{dx}$. You may need to first rearrange the equations for $u$ or $\frac{du}{dx}$ before substituting. Your integral should have no $x$’s anymore after subbing.
integrate as usual. Don’t forget “+C”
plug back in your $u$ formula and call it a day
(If computing a definite integral, then plug in upper and lower limits in for $x$, and subtract the results.)

$10(x-20)^{\frac{1}{2}}+C$

Let $u=3x+1$

First find an “inside function” and let it be called $u$.
Find the derivative of $u$, $\frac{du}{dx}$
Find where the expressions you have for $u$ and $\frac{du}{dx}$ appear in the integral and replace them in the integrand with $u$ and $\frac{du}{dx}$. You may need to first rearrange the equations for $u$ or $\frac{du}{dx}$ before substituting. Your integral should have no $x$’s anymore after subbing.
integrate as usual. Don’t forget “+C”
plug back in your $u$ formula and call it a day
(If computing a definite integral, then plug in upper and lower limits in for $x$, and subtract the results.)

$\frac{2(3x+1)^{\frac{1}{2}}}{3}+C$

Let $u=x^3+\frac{3}{2}x^2$

First find an “inside function” and let it be called $u$.
Find the derivative of $u$, $\frac{du}{dx}$
Find where the expressions you have for $u$ and $\frac{du}{dx}$ appear in the integral and replace them in the integrand with $u$ and $\frac{du}{dx}$. You may need to first rearrange the equations for $u$ or $\frac{du}{dx}$ before substituting. Your integral should have no $x$’s anymore after subbing.
integrate as usual. Don’t forget “+C”
plug back in your $u$ formula and call it a day
(If computing a definite integral, then plug in upper and lower limits in for $x$, and subtract the results.)

$\frac{(x^3+\frac{3}{2}x^2)^\frac{2}{3}}{2}+C$

Let $u=\sqrt{x}+1$. It would also be helpful to convert radicals to fractional powers

First find an “inside function” and let it be called $u$.
Find the derivative of $u$, $\frac{du}{dx}$
Find where the expressions you have for $u$ and $\frac{du}{dx}$ appear in the integral and replace them in the integrand with $u$ and $\frac{du}{dx}$. You may need to first rearrange the equations for $u$ or $\frac{du}{dx}$ before substituting. Your integral should have no $x$’s anymore after subbing.
integrate as usual. Don’t forget “+C”
plug back in your $u$ formula and call it a day
(If computing a definite integral, then plug in upper and lower limits in for $x$, and subtract the results.)

$\frac{2(x^{\frac{1}{2}}+1)^3}{3}+C$

Previous Lesson

Back to Lesson

Next Topic

Business Calculus

How the Method Works

Recall the Chain Rule for Derivatives

(The Basic) U-Substitution Method for Antideriving

Making alterations to the \(\frac{du}{dx}\) Equation

Compute the following antiderivatives