$Project Greater Ed Logo$

Guessing Limits Using Tables

Business Calculus Left, Right, and Two-Sided Limits Guessing Limits Using Tables

Guessing Limits of Functions Defined by Rules Using Tables

Suppose we are given a function defined by a rule instead of a graph such as

$$f(x)=\frac{x^2+2x+1}{x+1}$$

Notice that $f(-1)$ is not defined because when you plug $x=-1$ into the rule, the denominator is equal to $0$ which gives us division by zero… which is bad/undefined. It very well may be the case that we simply have a “hole” in our function at $x=-1$ much like what we’ve seen before. To make this determination, we need to see if the two-sided limit exists at $x=-1$. However, without having the graph of the function handy, how can we go about this? (because there are some functions that you can’t have a calculator graph nicely for you, such as piecewise functions)

Guessing Left and Right-Hand Limits Using Tables

Let $f$ be a function. To compute the left-hand limit of $f$ at some $x$-value $x=c$, build a table with two columns: one for$x$-value inputs and one for corresponding $y$-value outputs. Then, select $x$-values that are slightly LESS than $c$ that get closer and closer to $c$ as you read down the list. Plug those into your function to get the $y$-value outputs that correspond with those $x$-values. Lastly, see if the $y$-values are getting closer and closer to some specific value. If they are, that $y$-value they are approaching is your guess at the limit.

To guess the right-hand limit, build your table in the same way, but with decreasing input $x$-values that get closer and closer to $x=c$ and are also greater than $x=c$.

If both the guesses for the right-hand limit and left-hand limit are the same, you therefore have a guess for the two-sided limit.

We show this method in action in the example below, which uses the function we introduced earlier.

Let’s start with our left-hand limit table. See below. Note that since we are trying to compute $\lim_{x\rightarrow -1^-} f(x)$ (i.e. the left-and limit) we want to choose $x$-values that are slightly less than $x=-1$ and that also get closer to $x=-1$ as you read down the table. Plug those into the rule and see where the $y$-values are going.

$x$	$y=\frac{x^2+2x+1}{x+1}$
$-1.1$	$-0.1$
$-1.01$	$-0.01$
$-1.001$	$-0.001$
$-1.0001$	$-0.0001$

It appears that as the $x$-values approach $x=-1$ from the left, the $y$-values are getting closer and closer to $y=0$ (from below; we are getting less and less negative), so that will be our guess for the left-hand limit of $f$ as $x\rightarrow -1$. That is:

$$\lim_{x\rightarrow -1^-}\frac{x^2+2x+1}{x+1}=0$$

Now, we do the same thing with the right-hand limit, but instead of plugging in $x$-values that are less than $x=-1$, we plug in values that are larger than it, that are decreasing and getting closer to $x=-1$. See the table below!

$x$	$y=\frac{x^2+2x+1}{x+1}$
$-0.9$	$0.1$
$-0.99$	$0.01$
$-0.999$	$0.001$
$-0.9999$	$0.0001$

As we can see, as $x\rightarrow -1^+$, the $y$-values are decreasing, getting really tiny the closer the $x$-values get to $x=-1$. So we would guess that the right-hand limit of $f$ is also $0$. Thus we would write

$$\lim_{x\rightarrow -1^+}\frac{x^2+2x+1}{x+1}=0$$

Since our guess for the right and left-hand limit are the same, we have a solid guess for the two-sided limit.

$$\lim_{x\rightarrow -1}\frac{x^2+2x+1}{x+1}=0$$

Why is it only a guess?

Why is it that we cannot simply use our tables to correctly determine a function’s limit at a given $x$-value? Simply put: because we might not be plugging in values close enough to the given $x$-value to know exactly what the function is doing incredibly close by.

For instance, suppose we had a function like the one graphed below and we wanted to compute the right-hand limit at $x=1$.

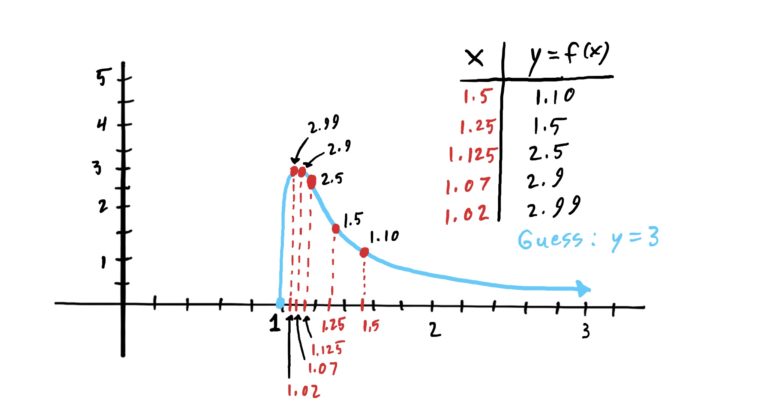
graph that dives down sharply when x is very slightly greater than 1

Notice that if we plugged in the five $x$-values you see, it would look like the $y$-values are headed toward $y=3$. We would need to plug in a few more $x$-values that were even closer to $x=1$ than the ones we chose to see that all the action is microns away from $x=1$.

Without a graph, we would never have known that the function dives down so sharply. Moreover, we wouldn’t know exactly how close to $x=1$ we’d need to choose our $x$-values to be so that we are not “tricked” into thinking the limit is $3$ instead of $0$. You would have to plug in an infinite number of $x$-values in order to not be “tricked” by the function. Hence, when using tables (or cutting to the chase and just plugging in a single number that is really close to the limit $x$-value instead of using tables) the best we can hope for is merely a guess.

Guess: $\lim_{x\rightarrow -2} 3x^2+1=13$

Guess: $\lim_{x\rightarrow -2} \frac{x^2-4}{x+2}=-4$

Guess: $\lim_{x\rightarrow -1} \frac{x^2+3x+2}{x+1}=1$

Guess: $\lim_{x\rightarrow 0} f(x)$ DNE

Guess: $\lim_{x\rightarrow 2} f(x)=4$

Guess: $\lim_{x\rightarrow 1} f(x)$ DNE

Previous Topic

Back to Lesson

Next Topic

\(x\)	\(y=\frac{x^2+2x+1}{x+1}\)
\(-1.1\)	\(-0.1\)
\(-1.01\)	\(-0.01\)
\(-1.001\)	\(-0.001\)
\(-1.0001\)	\(-0.0001\)

\(x\)	\(y=\frac{x^2+2x+1}{x+1}\)
\(-0.9\)	\(0.1\)
\(-0.99\)	\(0.01\)
\(-0.999\)	\(0.001\)
\(-0.9999\)	\(0.0001\)