$Project Greater Ed Logo$

Fundamental Theorem of Arithmetic and Factoring

Discrete Mathematics Prime Numbers and the Fundamental Theorem of Arithmetic Fundamental Theorem of Arithmetic and Factoring

(NOTE: It is definitely advised to watch the mini lecture video if you haven’t already).

When a number is composite, we often want to know what its factors are. Since every natural number is divisible by at least one prime number, it makes sense to look for the primes that divide our number. Better still, it might be more helpful to write our given number as a product of those primes. The following theorem tells us that we can always do this, and that there is only one way of doing this.

The Fundamental Theorem of Arithmetic

Every natural number aside from $1$ can be uniquely written as a product of primes (or nonnegative integer powers of primes), so that the prime factors are written in non-decreasing order.

You may have factored numbers into prime powers at some point in your life. The above theorem is what allows you to do this. Note that every natural number can be written as a product of primes, including primes themselves. In the latter case, the prime factorization is just that prime number itself!

Factoring Natural Numbers

To factor numbers, we use what are called factor trees.

To factor a number $n$ using a factor tree:

Write the number $n$ at the top of the page.
Find a divisor of $n$ and write that below $n$ and to the left, slightly. Draw a line from $n$ to this number.
Divide your $n$ by this factor, and write the result below $n$ but to the right. Draw a line from $n$ to this number.
Repeat the last two steps for each number you add to the tree until you have only primes at the bottom of the tree.
If you multiply all the primes at the base of your tree, you will (or should) get back $n$. So, write $n=$ a product of these primes, and simplify the expression so you have a product of prime powers.

Quick Example: Suppose we want to factor $n=84$. The factor tree is as follows:

So, by the factor tree above, we can write $84=2\cdot 2\cdot 3\cdot 7=2^2\cdot 3\cdot 7$.

Note

Your factor tree may look different from someone else’s, BUT, assuming you used the method correctly and write your prime powers in increasing order, your factorizations will be the same (by the uniqueness part of the Fundamental Theorem of Arithmetic).

Another Note (on Negatives)

If you are asked to factor a negative, you can use the exact same approach with factor trees as above. Note that if you have a number like $-30$, this is the same as $-1\cdot 30$. So, you can factor the $30$ as usual, and just put a $-1$ in front of your factorization to represent that the negative “comes along for the ride.”
Ex: $-30=-1\cdot 30=-1\cdot 2\cdot3\cdot 5$

$81=3^4$

$240=2^4\cdot 3\cdot 5$

$321=3\cdot 107$

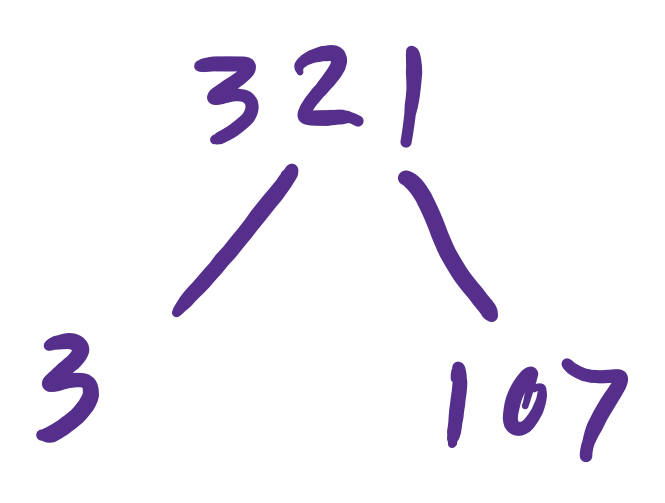
$1023=3\cdot 11\cdot 31$

$503$ is prime, so it is it’s own factorization.

Note that the primes that are less than $\sqrt{503}=22.42$ are $2,3,5,7,11,13,17,19$ and none of these primes divide $503$, so therefore $503$ must be prime, and primes are their own factorizations.

Previous Topic

Back to Lesson

Next Topic