First Derivative Test and Global Mins and Maxes
Identifying Global Mins and Maxes Using the First Derivative Test
Recall the definition of global mins and maxes of a function defined on an interval:
Essentially, a global max is where the function is “higher” than everywhere else. A global min is where the function is “lower” than everything else.
Now recall that we essentially defined local mins as \(x\)-values where the function is lowest when compared to points nearby. Similarly, local maxes are the \(x\)-values where the function is highest when compared to other points nearby.
Since local maxes are where the function is largest when compared to points close by, local maxes are candidates for global maxes. Similarly, since local mins are where the function is lowest when compared to points close by, local mins are candidates for global mins. The following image illustrates that local maxes are sometimes global maxes and that local mins are sometimes global mins.
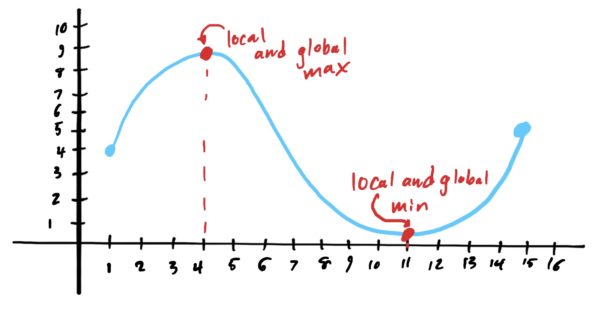
However, since we usually seek to determine local and global mins and maxes of a function defined on an interval, we might run the risk of a function having its mins and maxes at the endpoints of the interval, such as in the graph below.
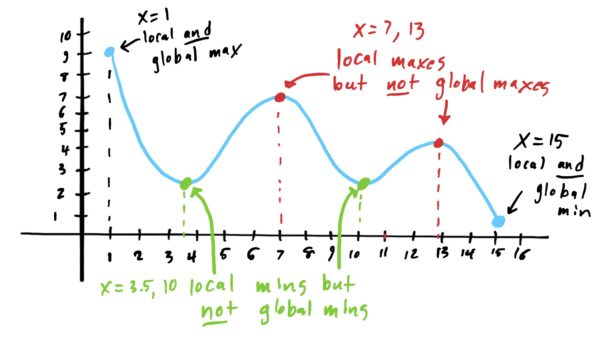
Recall that every global min is also a local min, and that every global max is a local max, but it is not true the other way around. This gives us a useful starting point for determining global mins and maxes of an entire function (especially when we don’t have a graph): find all local mins and maxes, and determine which produce the highest and lowest \(y\)-values from the original function. Since we are primarily working with smooth functions, our method for determining our global mins and maxes is even easier.
The reason this works is fairly logical: Suppose that none of your critical points are global maxes/min. Then, there is another \(x\) value where \(f\) attains its local max/min (because \(f\) is defined on a closed interval). But since global max/mins are also local max/mins then that means our list of possible mins and maxes (i.e. our critical points and endpoints) is incomplete; i.e. we missed a critical point. Assuming we found all critical points to start with, it is not possible to “suddenly have another one.” Therefore our global min or max must occur at a critical point or an endpoint of the interval.
We first find the critical points of \(f\). Super easy. Just take the derivative, set it equal to zero, and solve for \(x\). See below.
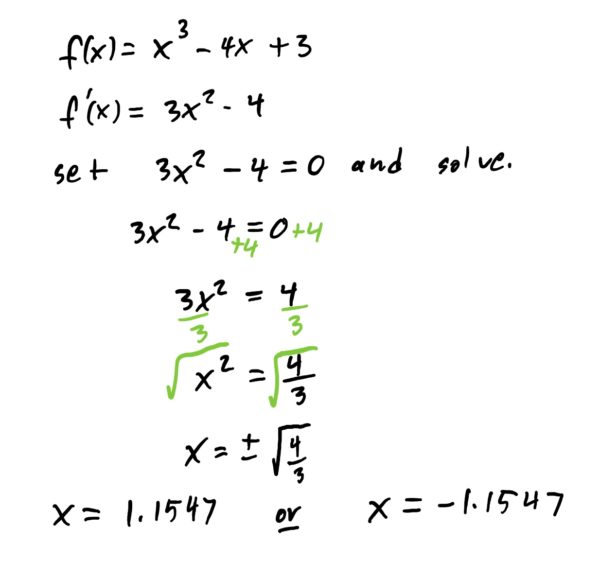
Now that we have our critical points, we know that they are either a local min or max (or neither). If we can determine that one is a global min or max, we get that it will be a local min or max by default.
At this point, to find our global mins and maxes of the function on the interval provided, we plug each of our critical points into the function, along with the endpoints \(x=-2\) and \(x=3\), and see which produce the largest and lowest \(y\)-values. The results are in the table below.
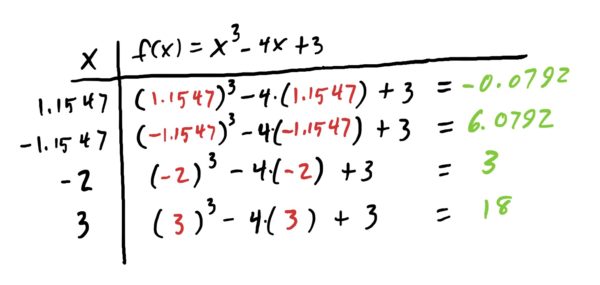
Now that we have \(y\)-values associated with all candidates for global mins and maxes, all that’s left is to pick out the \(x\) value with the biggest \(y\)-value (for the global max) and the \(x\)-value with the least \(y\)-value for the min.
Global min: \(x=1.1547\). Global Max: \(x=3\).
Its worth noticing that the min occurred at a critical point (i.e. where the derivative is zero) whereas the max occurred at \(x=3\): the boundary/interval endpoint.