Finding Extrema by Graphing
Identifying Extreme Values
As hinted at in the lesson primer, our goal is to identify the extreme values of a function; i.e. it’s highest and lowest points and where they occur. Furthermore, we are also interested in determining when a function achieves a “local top” or “local bottom,” which are essentially points that are higher (or lower) than all other points close by. We will investigate the precise definition of both absolute/global extrema and local extrema first by using graphs.
Essentially, a global max is the input \(x\)-value that produces the highest \(y\)-value the function can attain. A global min is an \(x\)-value where \(f\) produces the lowest possible output.
Notice also that the definition said “an absolute min/max,” indicating that there might be several. This can happen. There might be several \(x\)-values that produce the same “highest \(y\)-value” or the same “lowest \(y\)-value.”
Let’s see if we can identify the absolute/global mins and maxes of the graphed function below.
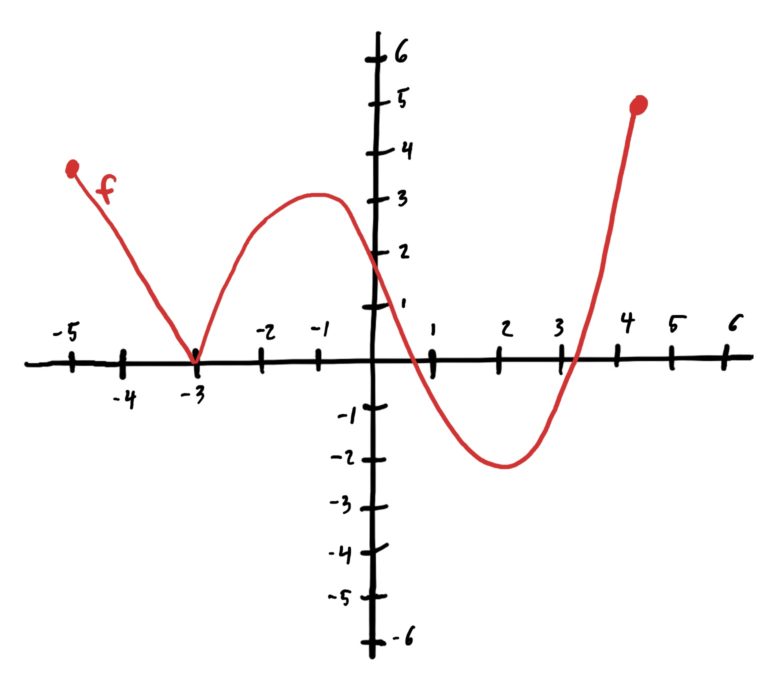
To find the global min(s), we are looking for the \(x\)-value of all points where \(f\) is lowest. \(f\) has a global min at \(x=2\). The minimum value of \(f\) is therefore \(f(2)=-2\). There are no other \(x\)-values that produce this output, so \(x=2\) is the only global min.
To find the global max, we are looking for the \(x\)-value of all points where \(f\) is highest. \(f\) has a global max at \(x=4.25\)ish. The maximum value of \(f\) is therefore \(f(4.25)=5\). \(x=4.25\) is the only global max.
In the above example, you may have been tempted to think that \(x=-5\) was a global max, or that \(x=-3\) was a global min. This is likely because the point at \(x=-5\) was higher than all \(f\)’s \(y\)-values close by. Similarly for \(x=-3\), producing a \(y\)-value lower than the other \(y\)-values close by. Still, these do not produce the absolute highest and lowest (respectively) values which is what we were after. However, this idea of “biggest and smallest close-by ” is an important one that we will now address.
Local Mins and Maxes
In the graph below, we exhibit a local maximum at \(x=2\). Note that \(x=2\) is NOT the absolute maximum of \(f\), but it is a local max because there is an interval containing \(x=2\) so that \(f(2)\geq f(x)\) for all \(x\in I\) (i.e. \(f(2)\) is higher than every other \(y\)-value produced by \(x\)-values in \(I\)).
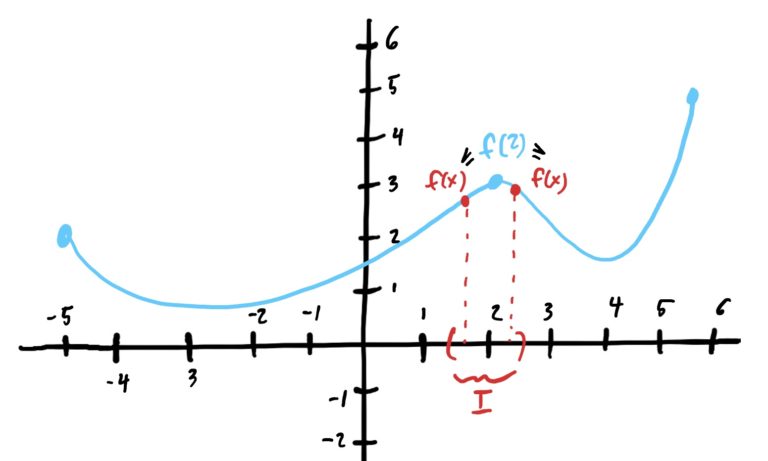
Again, its usually best just to think of local mins as the location of the highest and lowest points “nearby” (respectively).
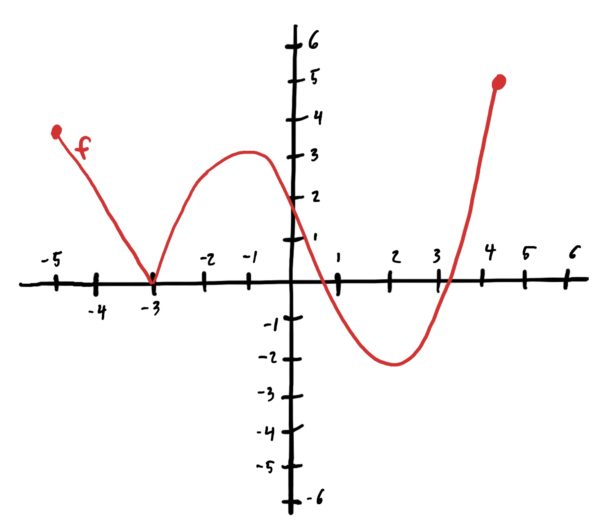
To find the local mins, we are looking for points on the graph that are lower than all other points “close by” and writing down their \(x\)-values. This gives us \(x=-3\) and \(x=2\).
Similarly, to find the local maxes, we are looking for points on the graph that are higher than all other points “close by” and writing down their \(x\)-values. This gives us \(x=-5\), \(x=-1\) and \(x=4.25\).
You can verify that these are indeed local mins by choosing any sufficiently small interval around either \(x\)-value and comparing the \(y\)-values of the points in that interval to those at the local extrema. Mins are lower and maxes are higher than those \(y\)-values of nearby points.
Important note: Global mins are also local mins. Global maxes are also local maxes. Don’t forget those in your lists.
Holey Graphs, Batman! When There Are No Mins or Maxes
Some graphs look like they should have mins or maxes at certain \(x\)-values, but in fact do not. We show this in the quick example below.
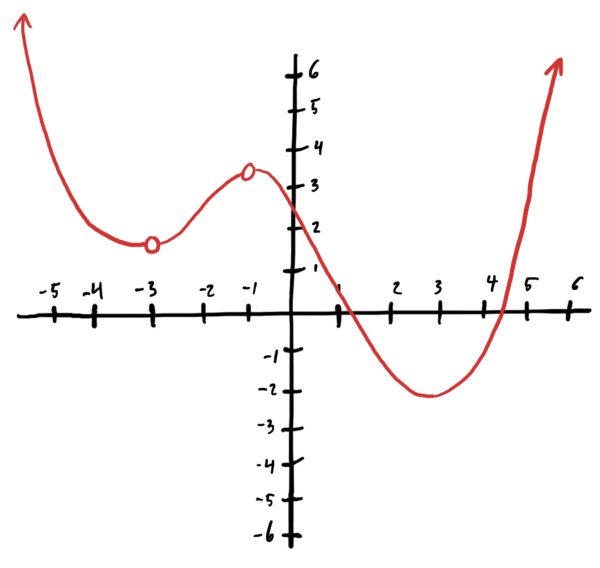
Note first that there are no maxes of any kind! You might be thinking that \(x=-1\) is a local max, but unfortunately \(f\) is not defined at \(x=-1\), so there isn’t even a \(y\)-value there for it to be bigger than others nearby! Also, note that the arrows on the ends of the graph indicate that the graph shoots into the sky in that general direction without stopping. So, again, this function has no maxes of any kind!
What about mins? We do get a min at \(x=3\). This is both a local and global min. Note that \(x=-3\) is NOT a local min because, like \(x=-1\) above, the function doesn’t have a \(y\)-value there. So there is nothing to compare nearby \(y\)-values to.
Final lists: local and global min: \(x=3\). local max: none. global max: none.
Find and classify the local and absolute extrema of the functions below
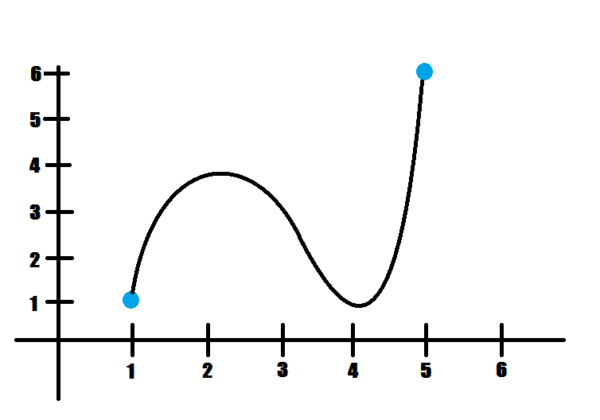
Determine the \(x\)-values where the function is largest and smallest. Don’t just look at the big dots!
Local absolute mins at \(x=1,4\), local and absolute max at \(x=5\).
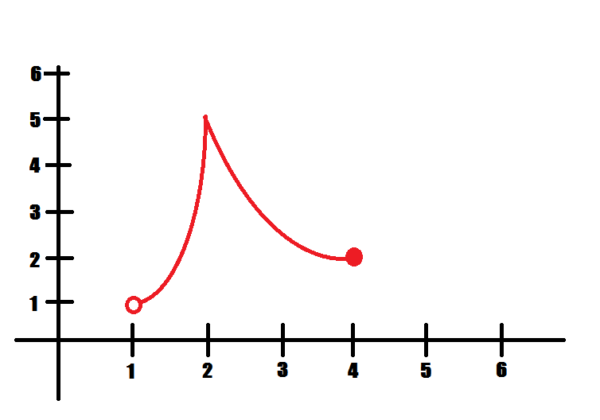
Since our function is not defined at \(x=1\), can it have a min there? Note, however, that our function is defined at \(x=4\).
local min at \(x=4\), absolute (and therefore local) max at \(x=2\). No absolute mins
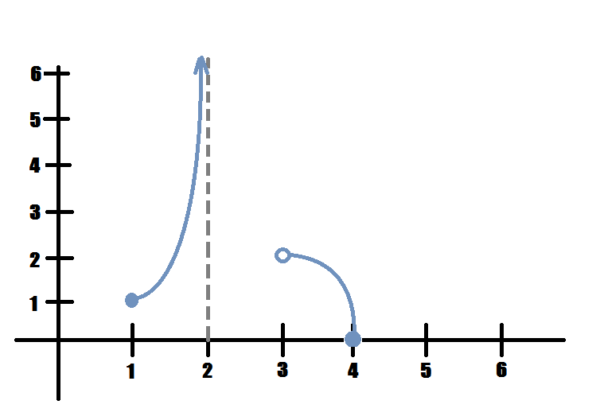
As we approach \(x=2\) on the left, the function shoots into the sky. Can we have an absolute max in this case?
local min at \(x=1\), absolute min at \(x=4\), no local or absolute maxes
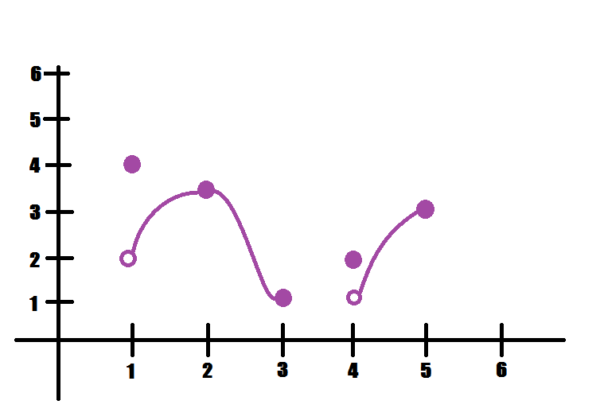
Are the points at \(x=1,4\) higher or lower than everything else nearby? Be careful!
absolute (and therefore local) min at \(x=3\), absolute (and therefore local) max at \(x=1\). Local maxes at \(x=2,4,5\)
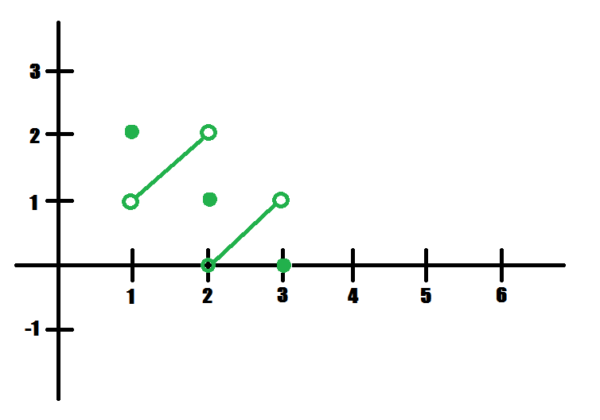
Is the point at \(x=2\) higher or lower than all points nearby? Be careful!
Absolute (and therefore local) mins at \(x=1,3,4\). Local min at \(x=2\). No local maxes.
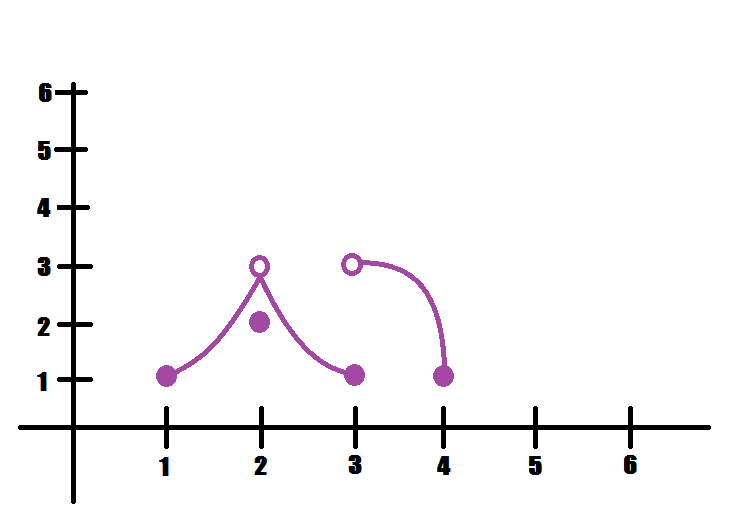
Are the points at \(x=1,3\) higher or lower than everything nearby?
Absolute min at \(x=3\). Absolute max at \(x=1\).
