Finding Derivatives as a Limit of an Average Rate of Change
Using Average Rates of Change to Find Instantaneous Rates of Change
Recall the definition of an average rate of change of a function on an interval:
Essentially, this formula gives you a “gist” of how much your function’s \(y\)-values changed from the start of your interval to the end of your interval (i.e. from your “starting \(x\)-value” to your “ending” \(x\)-value). It is also the slope of the secant line joining the points on your graph corresponding to the start and end \(x\)-values respectively. See graphical example below for a depiction of this idea.
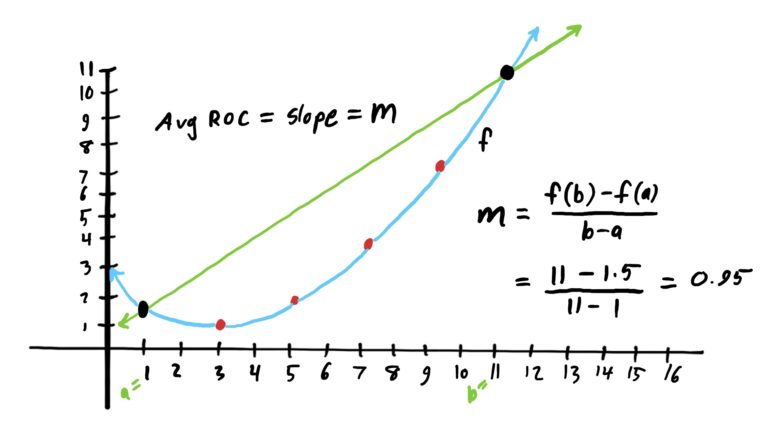
As the name indicates, an average rate of change is a RATE. It tells you how much the function’s \(y\)-values change based on a certain amount of change in \(x\). An average rate change can be thought of (at least colloquially) as the function’s “average speed” between two \(x\)-values. The higher the average rate of change, the “faster” the function is increasing between the start and end \(x\)-values.
The key with finding average rates of change is the fact we are using two endpoints: a start point and an endpoint. In computing the average rate of change we are comparing the start point to the endpoint. But what if we wanted to know exactly “how fast” the function is changing/moving at \(x=4\)? Is there a way to find the instantaneous average rate of change at exactly \(x=4\) (i.e. without having two endpoints, but only a single point to work with)?
The method: Bring your endpoints infinitely close together!
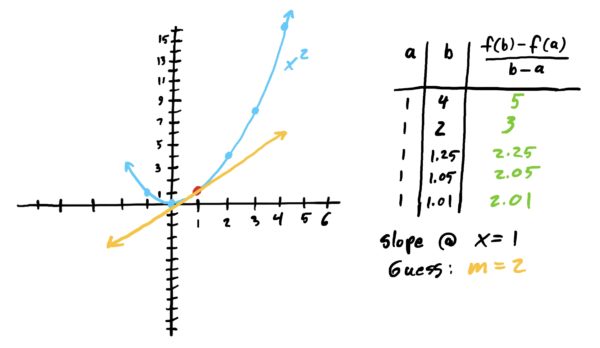
Remember when we introduced limits, we said that we can guess limits by generating a table of function \(y\)-values as the \(x\)-values got really, really close to some specific limit \(x\)-value? So too can we use this same approach to “guess” the instantaneous rate of change at a single point. We illustrate this idea with an example below.
Suppose \(f(x)=x^2\) and suppose also that we want to find the instantaneous rate of change of \(f\) at \(x=1\); i.e. we want to find the function’s “speed” at \(x=1\). We can do this by letting our starting point of our secant line be \(x=1\) and choose ending points that get progressively closer to \(x=1\) and see if we can determine what the rates of change approach. This is illustrated below.
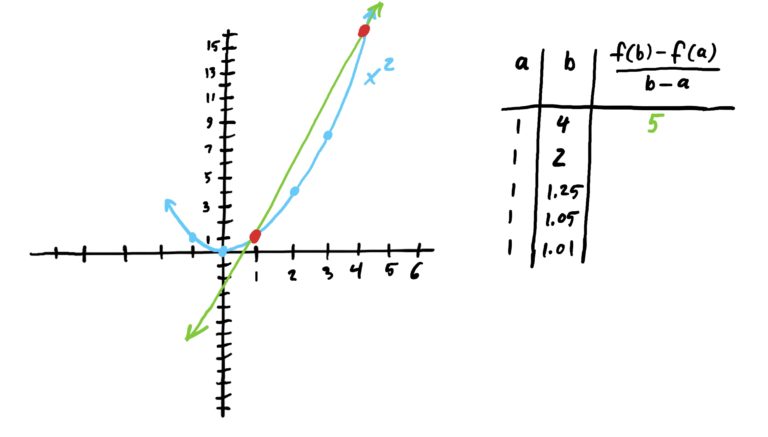
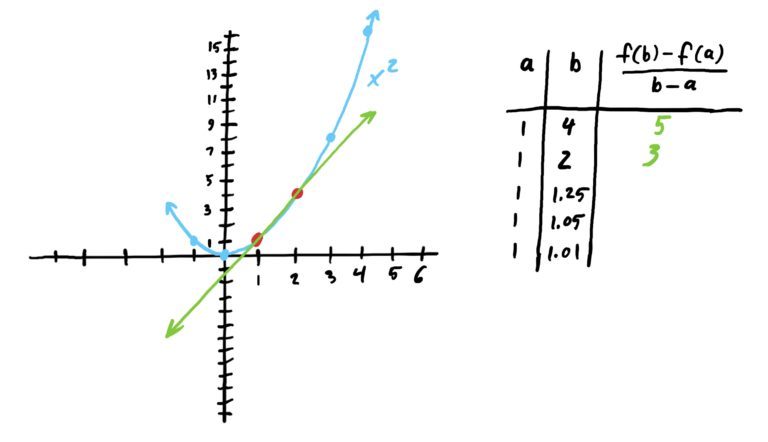
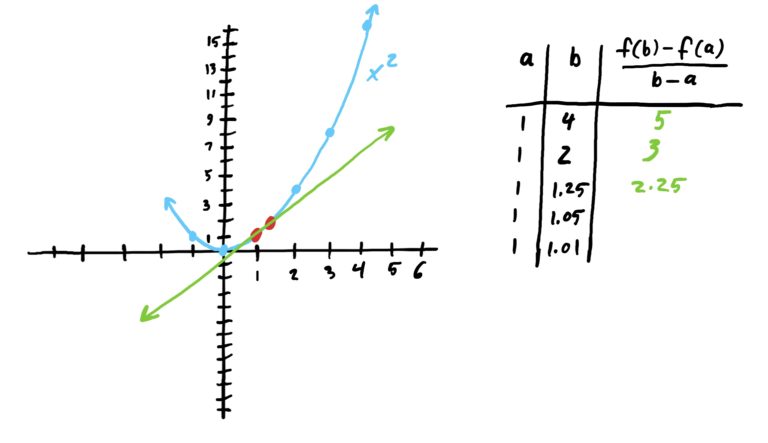
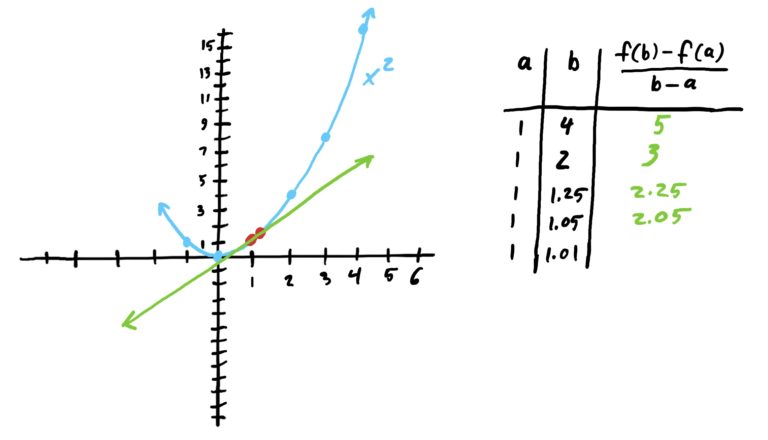
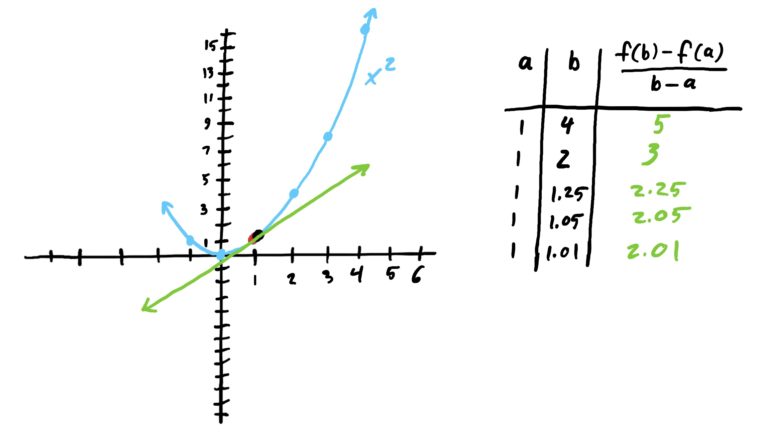
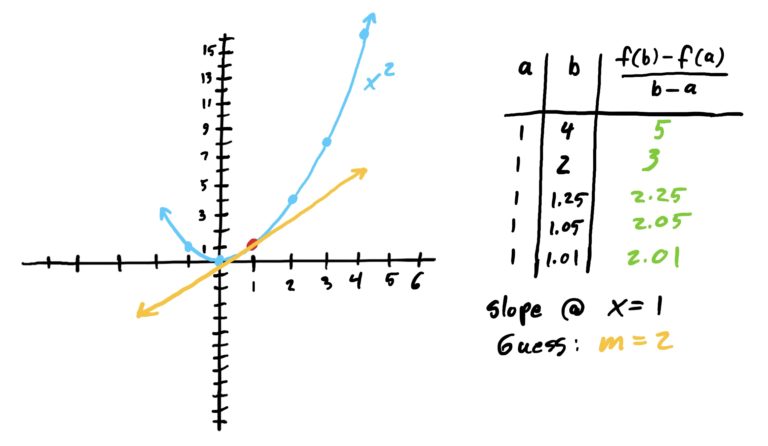
As we can see in the image sequence above, the slopes converge to \(m=2\) at \(x=1\). Thus, we have a really good guess for the instantaneous rate of change of \(f(x)=x^2\) at exactly \(x=1\), namely \(m=2\).
What we did above was the same process that we used when we introduced limits. Thus, if we want to determine an instantaneous rate of change at a specific \(x\)-value, then we can do so by computing a limit of average rates of change. This is fleshed out in the definition below.
Actually Computing Derivatives
When it comes to computing derivatives, we do NOT use the table method above. Since derivatives are nothing more than limits of average rates of change, we just apply whatever algebra and limits techniques we know in order to compute derivatives.
Let’s see if we can do this algebraically. See the algebra below. We do follow the steps given in the method above, but we carry the limit along for the ride until we are ready to take the limit at the end of the problem.
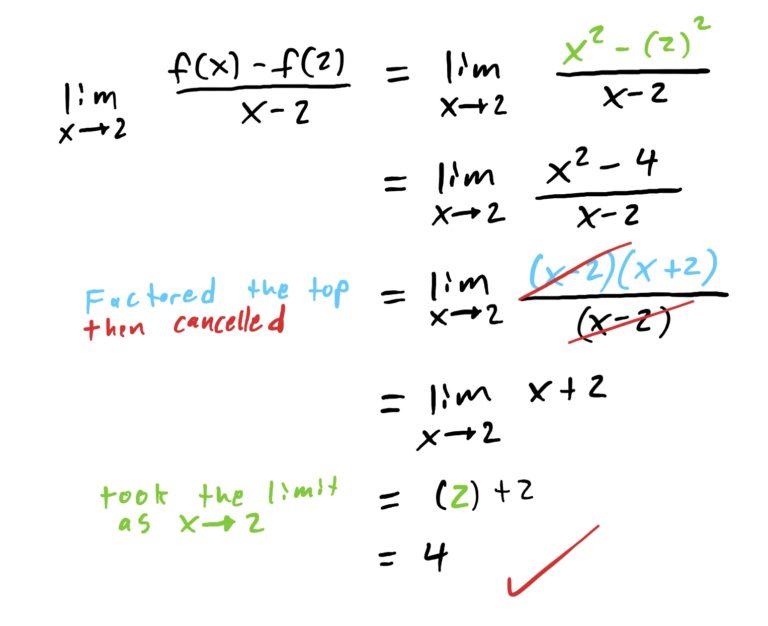
Note that we could NOT have taken the limit at the outset by plugging in \(x=2\) because that would make the denominator of the fraction zero. Can’t have division by zero, so we need to algebraically massage this expression a bit before plugging things in.
Finding the Equation of Tangent Lines
When you compute an average rate of change of a function between two \(x\)-values, you are computing the slope of the secant line joining the endpoints associated with those \(x\)-values. (See below).
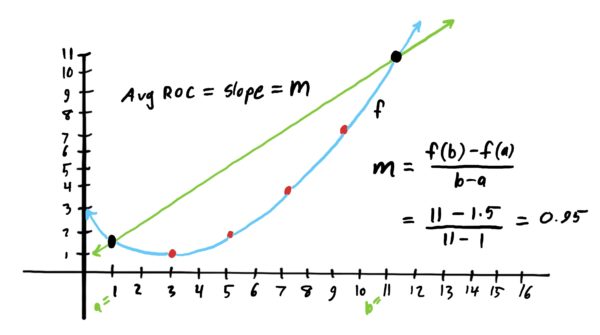
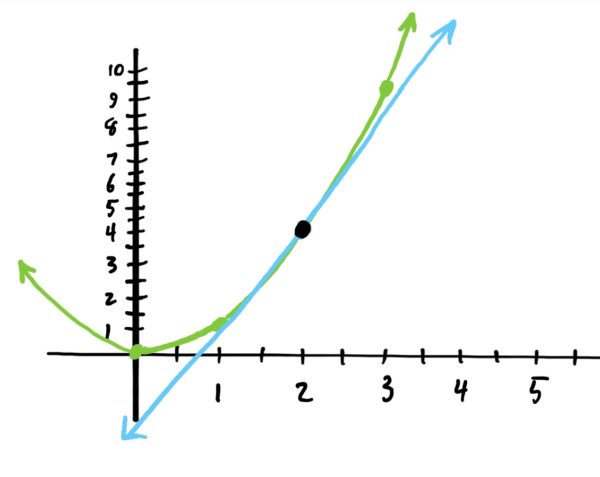
We then used the slopes of secant lines (i.e. average rates of change) to find the instantaneous rate of change of a function at a specific \(x\)-value. This instantaneous rate of change – i.e. the derivative of a function at a point – is the slope of the tangent line at the given limit \(x\)-value. See image below for this idea depicted.
Often we are interested in finding the equation of this tangent line. Recall that all that is needed to find an equation of a line are the slope of the line and a point on the line. All of this can easily be found using the function’s rule and the limit \(x\)-value provided.
Our goal is to find the equation of the line tangent to the graph at \(x=2\). This line is shown below.
To do this, we plan on using the point-slope formula for finding the equation of this line:
$$(y-y_0)=m(x-x_0)$$
To use this, we need a slope and a point on the line.
The slope \(m\) can be found from the derivative \(f'(2)\). We computed this in the derivative-finding example above. Specifically, we found that \(f'(2)=4=m\). Now we have the slope of the graph at exactly that point.
We now need the \(x\) and \(y\) value of a point on the graph of \(f\) at this point. We already know the \(x\)-value: \(x=2\). To find the \(y\)-value, we know that the line touching the graph and the function itself share the same \(y\)-value at the point where they touch, so we can find the \(y\)-value of this point by plugging in \(x=2\) into \(f\). This gives us \(y=f(2)=(2)^2=4\). So we have \(x_0=2\), \(y_0=4\), and \(m=4\). Plug all this into point-slope form to get
$$(y-4)=4(x-2)$$
Solving for \(y\) in this equation gives you the equation of the tangent line:
$$y=4x-4$$
Find the following derivatives using the limit definition
$$f'(c)=\lim_{x\rightarrow c} \frac{f(x)-f(c)}{x-c}$$
Note that in the problems below \(x_0=c\); i.e. the given \(x\)-value.