Finding a Function’s Average Value Using Integrals
Finding Averages of Specific \(y\)-Values
Suppose you want to find the average value of the numbers \(3.14\), \(5.5\), \(9.25\), and \(12.7\). To do this, you’d first add up the values, and then divide by the number of things you added up. Viz:
$$\frac{3.14+5.5+9.25+12.7}{4}$$
Similarly, if you wanted to find the average of 50 different values, you would do the same thing: just add up all the values and then divide by 50.
Now suppose we have a continuous function (i.e. a function without holes or jumps) like the one depicted below, and we wanted to find the average value of all the \(y\)-value outputs of the function from \(x=0\) up through \(x=4\)
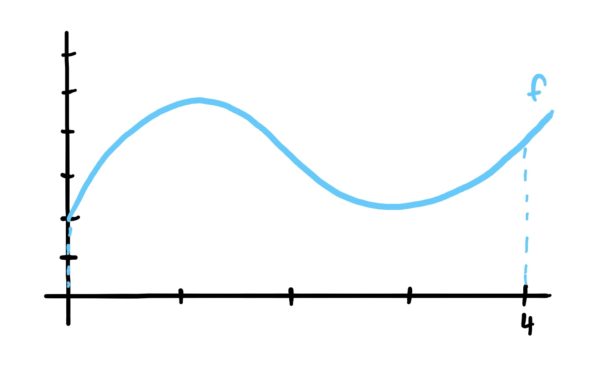
We can start by getting an estimate by picking 8 \(x\)-values that are all equally spaced between \(x=0\) and \(x=4\), plug them into our function, and then average their \(y\)-values.
However, since our function is continuous between \(x=0\) and \(x=4\), there are infinitely many \(y\)-values that were not taken into consideration when it came to computing the average value of the whole entire function on the interval provided. How could we adjust things so that we take into consideration all infinitely many of these \(y\)-values?
Well, if we use the idea of “taking limits of approximations” similar to what we did when we developed the definite integral for finding area, we can essentially continue to shove as many equally spaced \(x\)-values into the interval \([0,4]\) as we can, say \(n\) of them, and average the \(y\)-value outputs as usual.
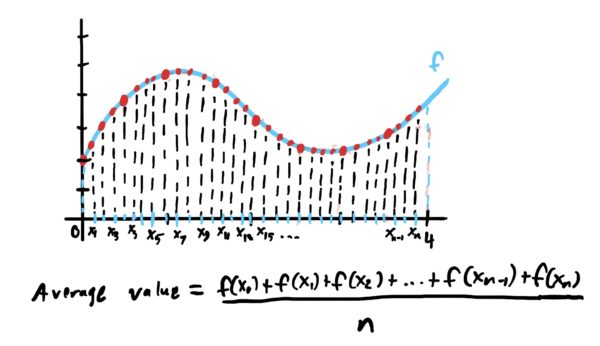
When we send the number of \(x\)-values to infinity (i.e. taking the limit of this average as \(n\rightarrow \infty\)) then we end up getting the following result.
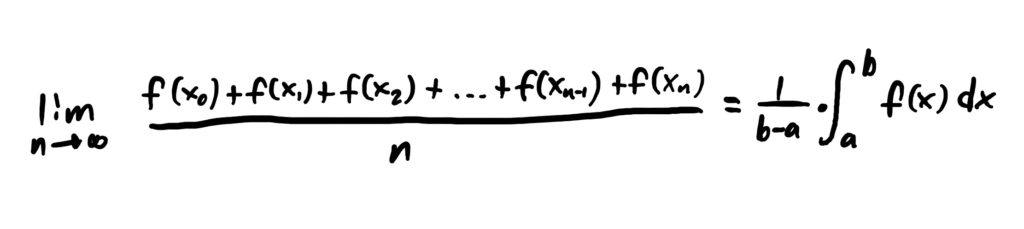
In general, one can find the average value of a continuous function by using the formula below.
If we think of the integral as “Summing up all the values of \(f\) from \(x=a\) to \(x=b\),” that would represent the numerator of an average value calculation. Since we can’t divide by infinity (because infinity isn’t a number), dividing by the size of the interval \([a,b]\) (when we multiply by \(\frac{1}{b-a}\)) gives us our denominator of an average value calculation. Examples of calculating the average value of a function on a given interval are given in the examples section below. Not too complicated at all.