$Project Greater Ed Logo$

Different Types of Graphs

Discrete Mathematics Graph Theory Basics Different Types of Graphs

Classifying Graphs Based on Certain Characteristics

Because graphs are so general and can be used to model many different phenomena, certain types of graphs with specific characteristics lend themselves well to one situation better than another. Furthermore, there are circumstances where solutions to graph-theoretic problems yield solutions to the situations they model. Here we study several common types of graphs that one encounters frequently both in theory and in practice.

Simple Graph

A graph $G$ is simple if it has no loops or parallel edges.

In a simple graph, edges can be identified with (or written as) a set containing their endpoints.

Complete Graph

A complete graph (on $n$ vertices), denoted $K_n$, is a simple graph such that every pair of vertices are adjacent.

Bipartite and n-Partite Graph

A bipartite graph is a simple graph whose vertices can be divided into two disjoint sets such that no two vertices in the same set are adjacent.

An $n$-partite graph is a simple graph whose vertices can be divided into $n$ pairwise disjoint sets, such that no two vertices in the same set are adjacent.

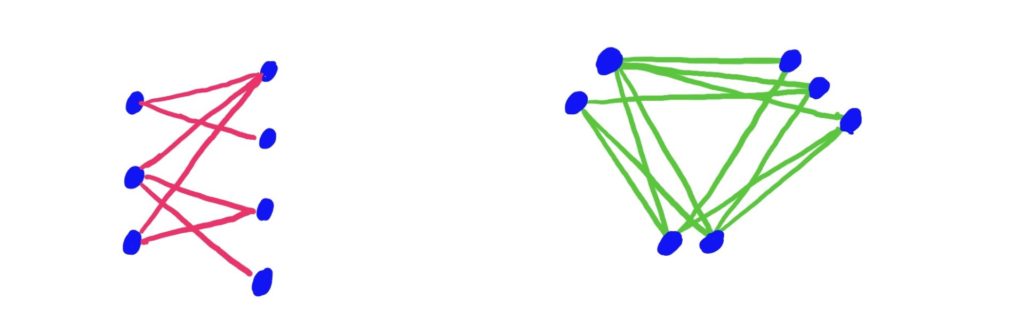
The graphs above were arranged so that the two (and three, respectively) sets of non-adjacent vertices were easy to see. More often, however, you need to do a bit of reorganizing yourself to see that the graph is $n$-partite!

Some graphs can be shown to NOT be bipartite, such as the following.

The above graph has what I call a “triangle” (also known as a $3$-clique). Because the vertices in the red triangle are all adjacent, I cannot place any pair of them in two separate sets without one connected pair being contained in one of the two sets! So this graph is NOT bipartite. (Is it $3$-partite?)

The strategy of isolating smaller parts of the graph in order to show why a property is or is not met is very common in graph theory as a whole.

Subgraph

A graph $H$ is a subgraph of a graph $G$ provided that $V(H)\subseteq V(G)$ and $E(H)\subset E(G)$.

One can think of subgraph as a small part of a “bigger” graph graph, just with some vertices and edges missing.

A Quick Note on Digraphs

Digraph (or Directed Graph)

A directed graph, or digraph, is a set of vertices $V(G)$ and a set of directed edges $E(G)$, where each edge is associated with an ordered pair $(v,w)$ of vertices, $v$ designating the start vertex, and $w$ designating the end vertex. Graphically this is represented as an arrow from $v$ to $w$.

Digraphs are arguably more useful than your standard graph in terms of applications (as they are more general). Digraphs can be used to represent travel paths (such as between cities), one-sided relationships between two objects (or people), algorithm steps, dependency structures, and boring old mathematically irrelevant flowcharts. Below is an example of how one could use a digraph to represent a relation!

Problem: Suppose $R$ is a relation defined by the set $R=\{(1,3),(1,2),(3,1), (2,4),(4,3),(4,1)\}$. Draw a graph that represents this relation, so that each number is represented by a vertex and every ordered pair is represented by directed edge.

The graph helps us easily determine whether or not a given element is related to another. For instance, it is easy to tell from the graph that $1$ is related to $2$ and $3$ via $R$.

A Few Remarkable Remarks (don’t kill me)

Because of the very general nature of graphs and digraphs and how much power they have to represent relationships, and because mathematics is largely the study of relationships between objects, it is possible to prove a medley of theorems in unrelated areas of mathematics just by leveraging the power of graph theory and its results. Some of the problems attached to this lesson/module illustrate these connections.

$J$ is simple, but not complete.

The first and third vertices in the top row of vertices are not directly connected; i.e. there is no edge between them. A complete graph requires that every vertex be connected to all others (directly) by an edge.

Not Bipartite!

Note that $v_3$ is connected to $v_5$ and $v_4$. $v_1$ is connected to $v_4$ and $v_6$. So, if you try to put $v_1$ and $v_3$ in group $1$, (in order to try to make this bipartite) this forces vertices$v_6$, $v_5$, and $v_4$ to be in the second group. $v_5$ and $v_4$ are adjacent, and neither can be moved to the other grouping (because one of the two is connected to either $v_3$ or $v_1$. (Try drawing this situation yourself!)

Similarly, if you try to put $v_1$ and $v_3$ in grouping $1$ and $2$ respectively, this forces $v_5$ and $v_4$ to be in grouping $1$. But this cant work, because $v_1$ and $v_4$ are connected! This is depicted above.

This is an example of a graph that is not bipartite even though there is no “triangle” (or $3$-clique) subgraph within $K$.

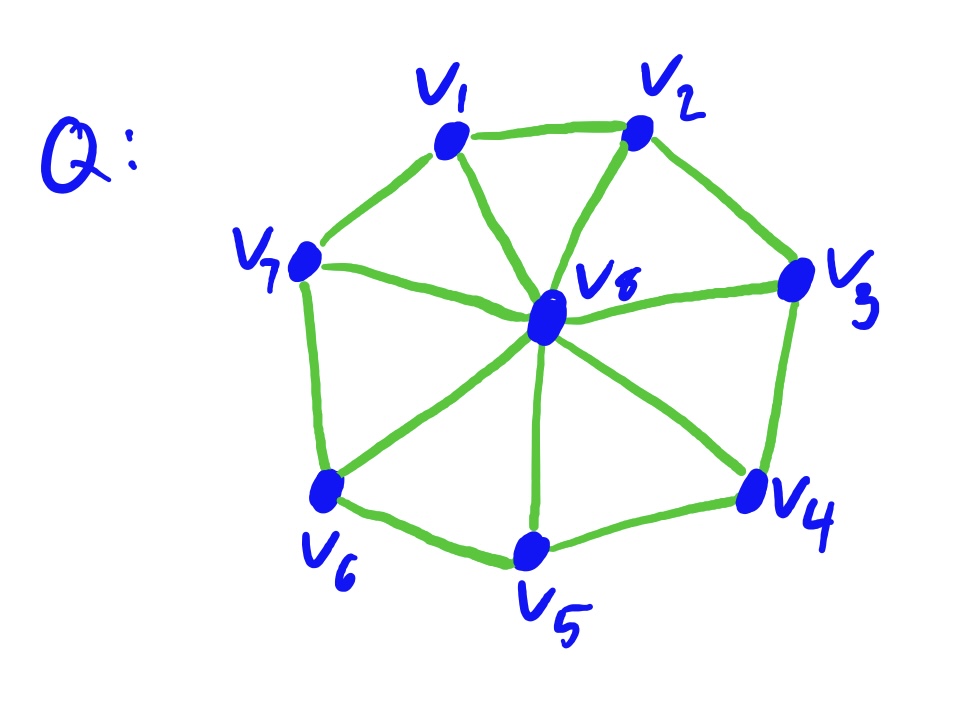
Not Tripartite!

For starters, since all vertices are adjacent to $v_8$ (except for $v_8$ itself) it follows that $v_8$ must be in a grouping all by itself. Now note also that all even-subscripted vertices connect to odd-subscripted vertices, so even-subscripted vertices must be in a grouping separate from the odd-subscripted vertices and separate from $v_8$ (for the reasons just described). But this causes a problem because $v_1$ is connected to $v_7$! So there is no way of organizing all these vertices into three groups so that no two vertices in each group is adjacent.

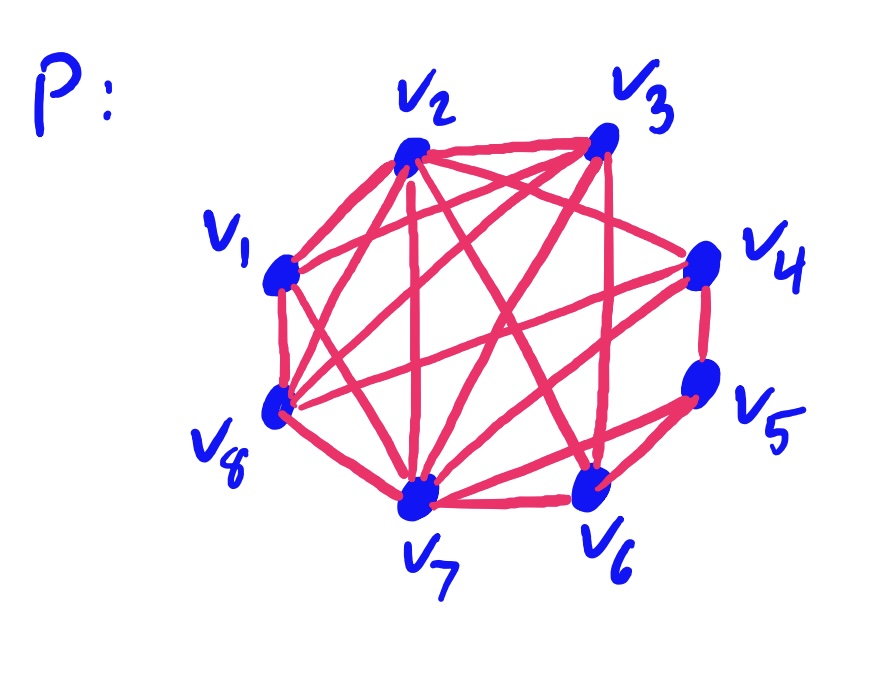
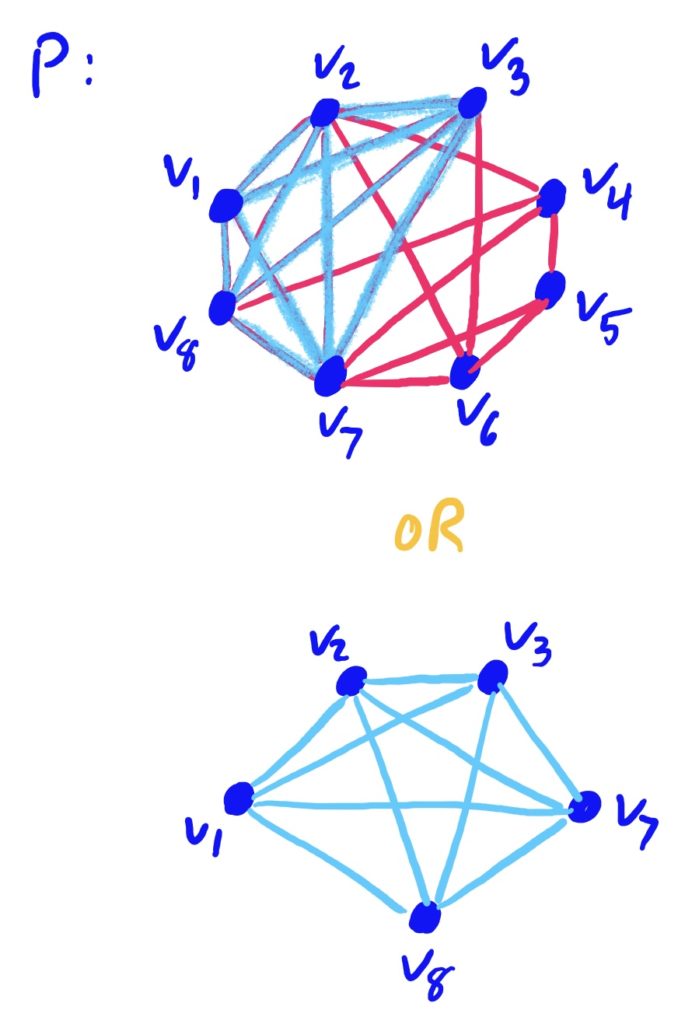
No need to make things more complicated than necessary! Clearly this graph is tri-partite, but it cannot be bipartite because all three vertices are connected to one another, so you cannot separate them into just two separate groupings where no two vertices in the same group are adjacent.

Nope! Can’t be! Each vertex is adjacent to three other different vertices. There is no way to place those other three vertices into three groupings “opposite” one another, so that no two vertices in the same grouping are adjacent. Try drawing this yourself to see what I mean!

Previous Topic

Back to Lesson

Next Lesson