Converting from Decimal to Binary and from Binary to Decimal
Hearkening Back…
When you first learned about numbers bigger than 10, such as the number \(4123\), what did each of the digits \(4,1,2,\) and \(3\) represent?
If you recall, the \(3\) represents the “\(1\)’s digit” or how many \(1\)’s you have. The \(2\) represents how many \(10\)’s you have (or how many groups of ten \(1\)’s you have). The \(1\) represents how many \(100\)’s you have (or how many groups of ten \(10\)’s you have). Finally, the \(4\) represents how many \(1000\)’s you have (or how many groups of ten \(100\)’s you have). Using this idea, we can expand \(4123\) so it is written as a combination of \(1\), \(10\), \(100\), \(1000\):
$$\begin{align}4123&=4\cdot 1000+1\cdot 100+ 2\cdot 10+3\cdot 1\end{align}$$
Note that each of \(1,10,100,\) and \(1000\) are all powers of \(10\), so we can rewrite the above as follows:
$$\begin{align}4123&=4\cdot 10^3+1\cdot 10^2+2\cdot 10^1+3\cdot 10^0.\end{align}$$
When numbers are written so that they can be broken down into sums of powers of \(10\), we say that number is a decimal number (where the prefix “deci-” means “ten”), or base 10. Digit positions correspond to powers of \(10\), where each of the powers of \(10\) you see are called the place values of the digit positions. As mentioned before, the digit in each position indicates how many of each power of ten you have.
Representing Numbers in Binary, or “Base 2”
Computers, fundamentally, are nothing more than a complicated collection of billions of “on/off” switches. And all computers really do, fundamentally, is turn these switches on and off in specific ways to accomplish everything that we take for granted.
We represent these different “On/Off” states of these switches using bits, or “1’s and 0’s.”
Before a computer can do anything, or perform any operation, all instructions, data, and input must be converted into a sequence of on/off states, which we can represent with a list of bits. Such a list is called a bit string. Example:
$$\begin{align}101011000101000001011111010101101011010111101011\end{align}$$
Each bit string represents a panoply of different information, and what it represents is entirely dependent on the context in which it is being used. For example, the above bit string can represent some decimal number; it also could represent an instruction for the computer to carry out. It also could represent an entire computer program, or a sentence written in Spanish. Regardless of what such a bit string represents, a computer fundamentally only performs operations on these \(1\)’s and \(0\)’s.
Furthermore, technically speaking, computers are doing various forms of arithmetic on these bit strings to perform many of the operations that a computer usually demonstrates. Many of these forms of arithmetic can be boiled down to the traditional “addition,” “subtraction,” “multiplication,” and “division,” of numbers. As was implied above, bit strings can represent numbers. Conversely, numbers can be represented by bit strings. Hence the following definition.
Note that “base” number (like “base 2” above) indicates how many digits/symbols are needed to represent a given number. It is possible to write numbers in bases other than 2 and 10. When writing a number in a base other than base 10, we use a subscript listing the base after the number is written. For example, the binary representation for the (base 10) number \(13\) would be written \(1101_2\).
When a number is written in base 10, each place value corresponds to how many powers of \(10\) you have. With binary numbers, each place value corresponds to how many powers of \(2\) you have. To compare, the digits in the number \(4123\) represent 3 \(1\)’s, 2 \(10\)’s, 1 \(100\), and 4 \(1000\)’s.

We can also represent the number \(4123\) in binary (or base 2) as \(1000000011011\) , where each digit represents the number of powers of \(2\) you have. Viz:

This leads to the next idea!
Converting a Binary Number to Decimal
Since the numbers in each position of a number written in base 2 (or any base for that matter) represent how many of each place value you have (in this case powers of 2), we can easily convert from binary or any other base to decimal by adding up the number of powers of the base we have in each place value.
So, looking at the binary number \(1101101_2\), we have the correspondence of each bit with each place value, as depicted below.

To write this in decimal form, since we have one \(2^0=1\)’s, zero \(2^1=2\)’s, one \(2^2=4\)’s, etc. we can sum up the powers we have at least one of. Viz:
$$\begin{align}1101101_2&=1\cdot 2^6+1\cdot 2^5+0\cdot 2^4+1\cdot 2^3+1\cdot 2^2+0\cdot 2^1+1\cdot 2^0&=109\end{align}$$
How to Convert a Decimal Number to Binary
Suppose you have a very large pile of potatoes and you want to determine how many potatoes you have (using our usual decimal number system). What you could do first is divide your potatoes into groups of 1000 (since you don’t have enough potatoes to form larger power-of-10 groups; i.e groups of 10000), and count the number of groups of 1000 you have, leaving the remainder potatoes (that are too few to form a group of 1000) off to the side.

Then, with the remainder potatoes, while you can’t form a new group of 1000, you can form a few groups of 100. So, you divide your remaining potatoes into as many groups of 100 as you can and then leave the remainder off to the side.

Finally, with the remainder potatoes, while you can’t form any more groups of 100, you can divide your remaining potatoes into a few groups of \(10\) potatoes. Leave the remainder off to the side (since these cannot be put into any more power-of-ten groupings.)

This allows us to see that we have \(2327\) potatoes. The \(2\) in the \(1000\)’s digit represents how many times we could evenly divide up our pile into groups of \(1000\). The \(3\) in the \(100\)’s digit represents how many times we could evenly divide up our remainder pile into groups of \(100\). The \(2\) in the \(10\)’s digit represents how many times we could evenly divide up that remainder pile (of potatoes that couldn’t be grouped into 100’s) into groups of \(10\). What finally remains is the remainder of potatoes that could not be put into groups of \(10\).
To convert a number from its usual base 10 representation to binary (or any other base, for that matter), we can employ a similar grouping strategy, repeatedly dividing remainders (or number of potatoes) by progressively lower powers of \(2\) to determine how many groups of size \(2^1=2, 2^2=4,2^3=8, 2^4=16,\ etc.\) we have. This is illustrated in the following method.
(Note that this same procedure can be used to convert from base 10 to any other base; just change the \(2\)’s above to the new base)

The highest power of \(2\) that is smaller than \(2031\) is \(2^{10}=1024\) (since \( 2^{11}=2048>2031\)). The power of \(10\) indicates the number of “place-value slots” we need to represent \(2031\) in binary (base 2).

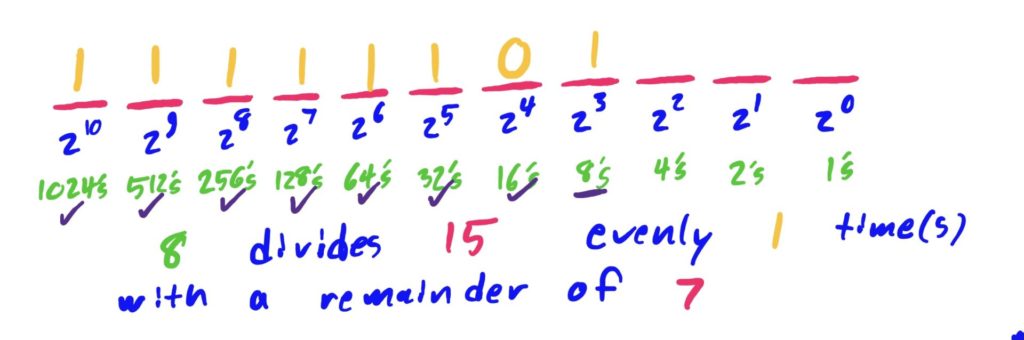
Note that \(2^{10}=1024\) evenly divides \(2031\) exactly once, so we have one group of size \(2^{10}\) and put a \(1\) in that slot. When dividing \(2031\) by \(2^{10}=1024\) we get a remainder of \(2031 \pmod 1024 =1007\).

Note that \(2^9=512\) evenly divides the last remainder \(1007\) exactly once, so we have one group of size \(2^9\) and put a \(1\) in the \(2^9\) slot. When dividing \(1007\) by \(2^9=512\), we get a remainder of\(1007 \pmod 2^512=495\).

Note that \(2^8=256\) evenly divides the last remainder \(495\) exactly once, so we have one group of size \(2^8\) and put a \(1\) in the \(2^8\) slot. When dividing \(495\) by \(2^8=256\), we get a remainder of\(495 \pmod 256= 239\).

The rest of the place-value slots are computed via the same procedure noted above as follows:
Note that it is possible to convert a decimal (base 10) number to any other base using exactly the same method! All that changes is you are doing all of the above in powers of the base you are converting to instead of powers of \(2\). For instance, you could convert the number \(2031\) to ternary (base 3) by replacing all powers of \(2\) in the procedure used above to powers of \(3\).
\(349\)
\(85\)
\(1111100_2\)
\(1010000000011_2\)