$Project Greater Ed Logo$

Computing Integrals Involving U-Substitution

Business Calculus Area, Continuous Accumulation, and Definite Integrals Computing Integrals Involving U-Substitution

U-Sub with Definite Integrals: Just one extra step

In general, for definite integrals such as

$$\int^1_0 x^2\ dx$$

we first compute the antiderivative of the integrand $x^2$ and then plug in the limits $x=1$ and $x=0$ and subtract the results. The same thing happens for integrals involving u-substitution. The only difference, really, is that you need to make sure you re-substitute in your $u$ at the end of the problem before you plug in your limits. This is illustrated in the following example. Note that there is a way to shortcut the method a bit and plug in your limits “early.” This will be demonstrated in the next section.

Notice first that the inside of the parentheses has a derivative of $15x^2$ which is close to what we have being multiplied on the outside of the parentheses; i.e. it has the same power on $x$. This indicates that $u$-substitution is needed here.

So let $u=5x^3+2$ and note that $\frac{du}{dx} =15x^2$. Since we have only $x^2$ being multiplied in the integrand, we need to algebraically solve for $x^2$ in the $\frac{du}{dx}$ equation. This gives us $\frac{1}{15}\frac{du}{dx}=x^2$. Now we can make our substitution. See below.

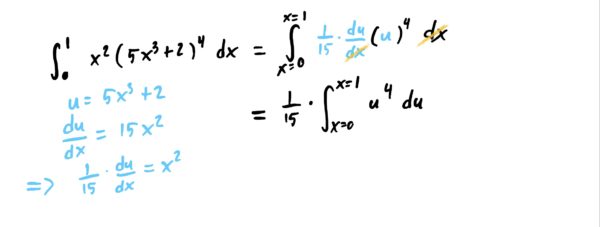
Note that the limits on the integral are still “$x$-limits” even though our integral now is entirely in terms of $u$. We will allow this for notational convenience. Now, simply carry out the integral as usual, integrating in terms of $u$ and then re-substitute in your $u=5x^3+2$ in at the end.

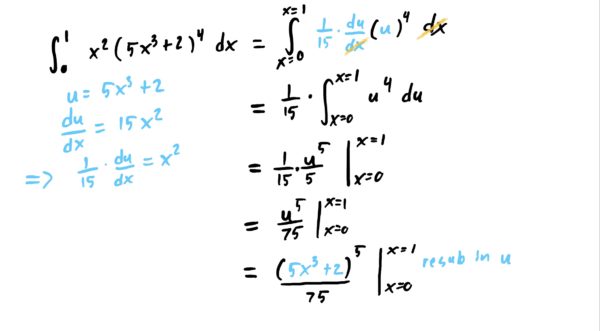
computing the integral up to resubstituting in u

Lastly, now that we have carried out the antiderivative completely, all that’s left is applying the fundamental theorem of calculus by plugging in the $x$-limits and subtracting the results. This gives you the result you see below.

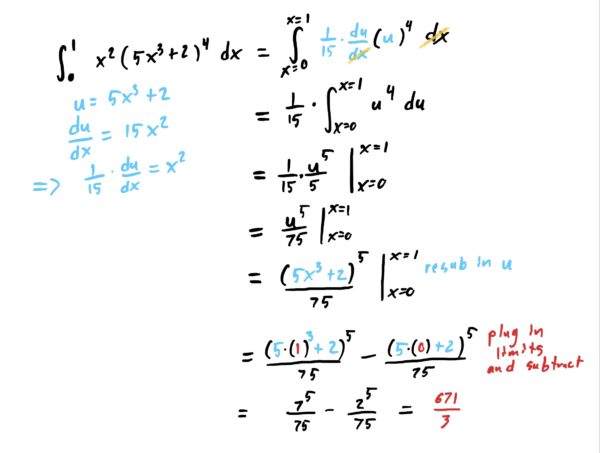
wrapping up the problem by pluggin gin the x-limits into the u and computing the differece

Plugging in Limits Early

Notice that in the last few steps of the previous example, we first re-substituted in $u=5x^3+2$, which basically meant replacing all “$u$-stuff” with “$x$-stuff.” Then we plugged in the $x$-limits in every place we saw an $x$. However, notice that all the $x$’s are contained in $u$.

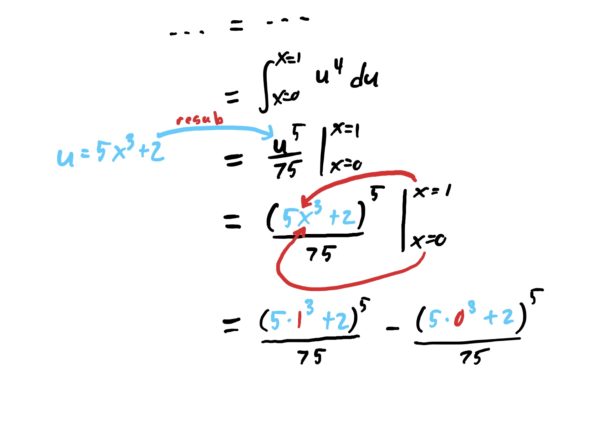
Since we always finish off a problem by “plugging $u$ back in, and then plugging numbers into $x$ which is inside $u$, we could more easily just combine these into one step and plug our $x$-limits into $u$ the moment we choose our $u$. This gives us the ability to exchange our $x$-limits for new snazzy $u$-limits. Below is the same example that we did before, but using this new strategy.

So let $u=5x^3+2$. Then, since at the end of the problem we’d be resubstituting $u=5x^3+2$ and plugging the $x$-limits in for $x$ which are contained in $u$, we can just plug ’em in right now to get $u$-limits. So, plug $x=1$ and $x=0$ into $u$ to get $u(1)=5(1)^3+2=7$ and $u(0)=5(0)^3+2=2$ respectively. These are now our new limits!

Note also that $\frac{du}{dx} =15x^2$. Since we have only $x^2$ being multiplied in the integrand, we need to algebraically solve for $x^2$ in the $\frac{du}{dx}$ equation. This gives us $\frac{1}{15}\frac{du}{dx}=x^2$. Now we can make all our substitution. See below.

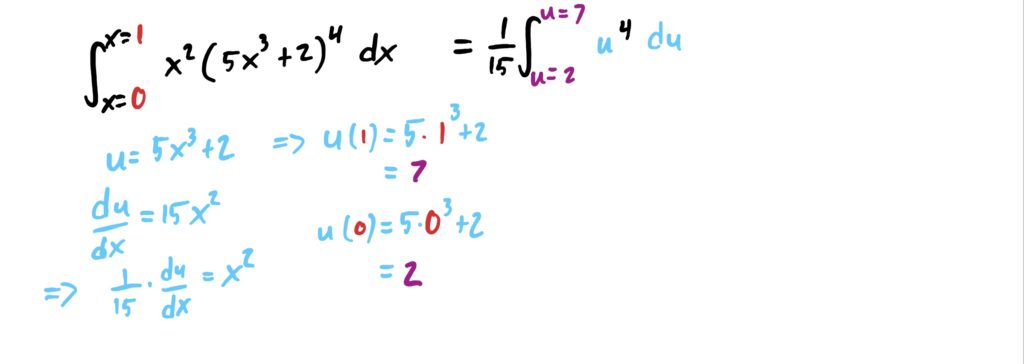
computing the new limits early, right after we declared what u is

Now, simply carry out the integral as usual, integrating in terms of $u$.

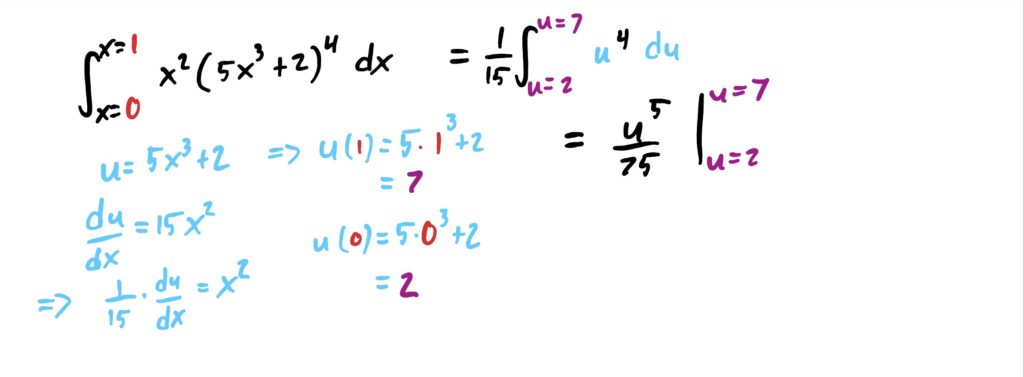
computing the integral in terms of u. Dont resubstitute the u!

Lastly, now that we have carried out the antiderivative completely, all that’s left is applying the fundamental theorem of calculus by plugging in the new $u$-limits and subtracting the results. We don’t need to worry about re-subbing in $u$ and then plugging in the $x$-limits, because we basically already did that earlier! This gives you the result you see below.

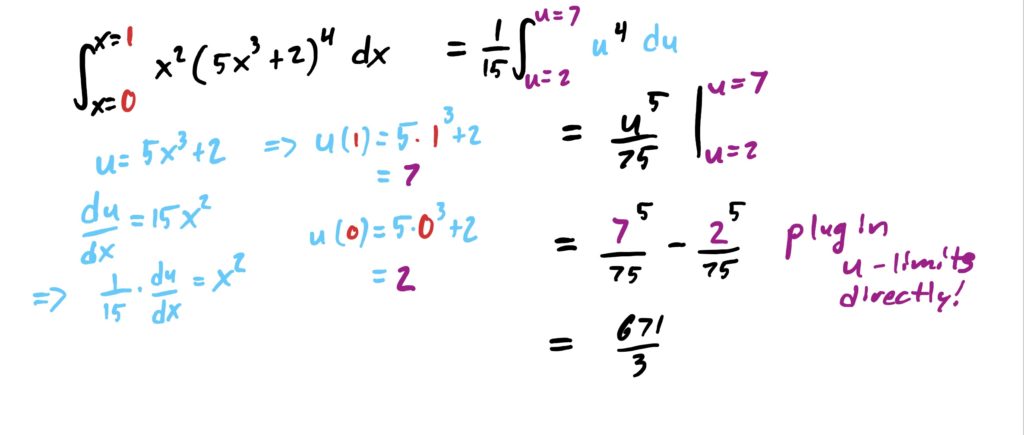
computing the integral and plugging in the new u limits directly

Compute the following definite integrals using the u-sub method.

Let $u=x^3+1$

Fundamental Theorem of Calculus (Part 2):

If $F(x)$ is an antiderivative of $f(x)$, then $\int^b_a f(x)\ dx=F(b)-F(a)$

First find an “inside function” and let it be called $u$.
Find the derivative of $u$, $\frac{du}{dx}$
Find where the expressions you have for $u$ and $\frac{du}{dx}$ appear in the integral and replace them in the integrand with $u$ and $\frac{du}{dx}$. You may need to first rearrange the equations for $u$ or $\frac{du}{dx}$ before substituting. Your integral should have no $x$’s anymore after subbing.
integrate as usual. Don’t forget “+C”
plug back in your $u$ formula and call it a day
(If computing a definite integral, then plug in upper and lower limits in for $x$, and subtract the results.)

$\int^2_1 3x^2(x^3+1)^{20}\ dx=\frac{9^{21}}{21}-\frac{2^{21}}{21}$

Let $u=2x+1$

Fundamental Theorem of Calculus (Part 2):

If $F(x)$ is an antiderivative of $f(x)$, then $\int^b_a f(x)\ dx=F(b)-F(a)$

First find an “inside function” and let it be called $u$.
Find the derivative of $u$, $\frac{du}{dx}$
Find where the expressions you have for $u$ and $\frac{du}{dx}$ appear in the integral and replace them in the integrand with $u$ and $\frac{du}{dx}$. You may need to first rearrange the equations for $u$ or $\frac{du}{dx}$ before substituting. Your integral should have no $x$’s anymore after subbing.
integrate as usual. Don’t forget “+C”
plug back in your $u$ formula and call it a day
(If computing a definite integral, then plug in upper and lower limits in for $x$, and subtract the results.)

$\int^2_{-1} (2x+1)^5\ dx=\frac{5^6}{12}-\frac{1}{12}$

Let $u=x^2+4$

Fundamental Theorem of Calculus (Part 2):

If $F(x)$ is an antiderivative of $f(x)$, then $\int^b_a f(x)\ dx=F(b)-F(a)$

First find an “inside function” and let it be called $u$.
Find the derivative of $u$, $\frac{du}{dx}$
Find where the expressions you have for $u$ and $\frac{du}{dx}$ appear in the integral and replace them in the integrand with $u$ and $\frac{du}{dx}$. You may need to first rearrange the equations for $u$ or $\frac{du}{dx}$ before substituting. Your integral should have no $x$’s anymore after subbing.
integrate as usual. Don’t forget “+C”
plug back in your $u$ formula and call it a day
(If computing a definite integral, then plug in upper and lower limits in for $x$, and subtract the results.)

$\int^2_1 \frac{x}{(x^2+4)^2}\ dx=\frac{-1}{16}+\frac{1}{10}$

Let $u=2x+1$

First find an “inside function” and let it be called $u$.
Find the derivative of $u$, $\frac{du}{dx}$
Find where the expressions you have for $u$ and $\frac{du}{dx}$ appear in the integral and replace them in the integrand with $u$ and $\frac{du}{dx}$. You may need to first rearrange the equations for $u$ or $\frac{du}{dx}$ before substituting. Your integral should have no $x$’s anymore after subbing.
integrate as usual. Don’t forget “+C”
plug back in your $u$ formula and call it a day
(If computing a definite integral, then plug in upper and lower limits in for $x$, and subtract the results.)

Fundamental Theorem of Calculus (Part 2):

If $F(x)$ is an antiderivative of $f(x)$, then $\int^b_a f(x)\ dx=F(b)-F(a)$

$\int^2_0 \frac{1}{\sqrt{2x+1}}\ dx=\sqrt{5}-1$

Let $u=x-1$. You will need to solve the $u$-equation for $x$.

First find an “inside function” and let it be called $u$.
Find the derivative of $u$, $\frac{du}{dx}$
Find where the expressions you have for $u$ and $\frac{du}{dx}$ appear in the integral and replace them in the integrand with $u$ and $\frac{du}{dx}$. You may need to first rearrange the equations for $u$ or $\frac{du}{dx}$ before substituting. Your integral should have no $x$’s anymore after subbing.
integrate as usual. Don’t forget “+C”
plug back in your $u$ formula and call it a day
(If computing a definite integral, then plug in upper and lower limits in for $x$, and subtract the results.)

$\int^2_1 x\sqrt{x-1}\ dx=\frac{16}{15}$

Let $u=x+1$. You will need to solve the $u$-equation for $x$.

First find an “inside function” and let it be called $u$.
Find the derivative of $u$, $\frac{du}{dx}$
Find where the expressions you have for $u$ and $\frac{du}{dx}$ appear in the integral and replace them in the integrand with $u$ and $\frac{du}{dx}$. You may need to first rearrange the equations for $u$ or $\frac{du}{dx}$ before substituting. Your integral should have no $x$’s anymore after subbing.
integrate as usual. Don’t forget “+C”
plug back in your $u$ formula and call it a day
(If computing a definite integral, then plug in upper and lower limits in for $x$, and subtract the results.)

$\int^1_0 \frac{x}{\sqrt[4]{x+1}}\ dx=\left(\frac{2^{\frac{15}{4}}}{7}-\frac{2^{\frac{11}{4}}}{3}\right) -\left(\frac{4}{7}-\frac{4}{3}\right)$

Previous Topic

Back to Lesson

Next Topic