$Project Greater Ed Logo$

Composing Two Function Rules

Precalculus Algebra Function Composition: Plugging One Function Into Another Composing Two Function Rules

Composing Functions Defined by Algebraic Rules

Recall that function composition is nothing more than taking the output of one function and plugging it into another function as input. Recall also that when a function is a defined by a rule, such as $f(x)=x^2+1$ the rule indicates what the function $f$ outputs based on the input $x$ (i.e. the rule tells you how the function produces it’s output). So, when it comes to functions defined by rules such as $f$ and $g$, the function composition $f(g(x))$ can be found by replacing every $x$ in the rule of $f$ with the rule of $g$.

Evaluating Function Composition of Functions Defined by Rules

To evaluate the composition $f(g(x))$, where $f$ and $g$ are functions defined by algebraic rules, simply replace all $x$’s in the rule of the “outer” function (namely $f$) with the rule for the inner function (namely $g$), and simplify if possible.

The result of composing two functions is referred to as the composition of the two functions.

To find $f(g(x)$, every place you see an $x$ in the rule for $f$, replace it with the rule for $g$. It is EXTREMELY helpful to keep the rule for $g$ in parentheses when substituting. Viz:

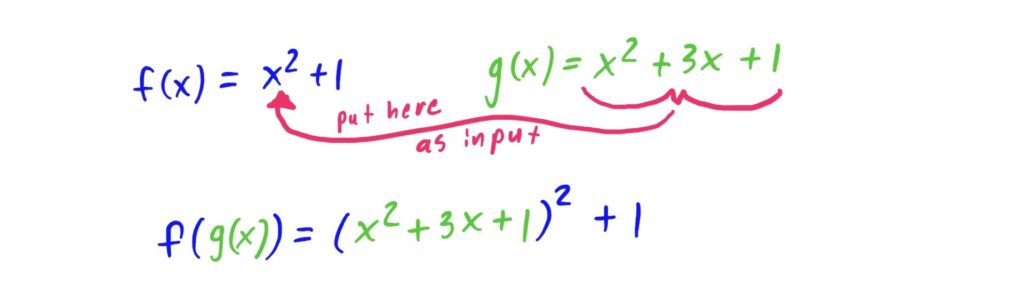
If you want to expand the square, go for it. To me this looks pretty simple, and simplification, like beauty, is in the eye of the beholder (or grader). From a technical standpoint, this problem is done.

Similarly, to find $g(f(x))$, every place you see an $x$ in the rule for $g$, replace it with the rule for $f$. Again, use parentheses when substituting!!! I promise it will save you dozens of points.

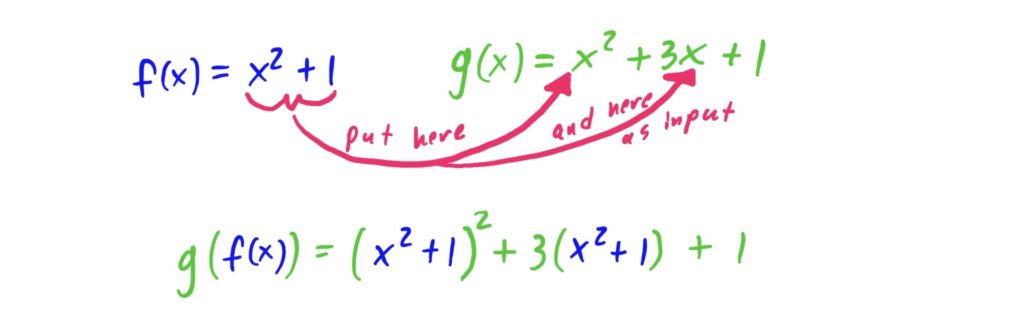
The above can then be expanded as

$$\begin{align} g(f(x))&=(x^2+1)^2+3(x^2+1)+1\\&=(x^4+2x^2+1)+(3x^2+3)+1\\&=x^4+5x^2+5\end{align}$$

And that is really as simplified as this gets.

Function Composition with Numerical Initial $x$-Value Input

To illustrate how the method above for composing functions is indeed just daisy-chaining two functions together, like an assembly line, feeding the output of one function into another function as input, consider the following example.

Recall that $f(g(1))$ is saying “find the output of $g$ on input $1$, and feed/plug that output into $f$ as input.” To this end we notice,

$$\begin{align}g(1)=(1)^2-4=-3\end{align}$$

and so

$$\begin{align}f(g(1))&=f(-3)\\&=3\cdot(-3)+1\\&=-9+1\\&=-8\end{align}$$

Similarly, to compute $f(g(2))$ first find $g(2)$ and plug the result into $f$ as input, just like the above. Viz:

$$\begin{align}g(2)=(2)^2-4=0\end{align}$$

And so,

$$\begin{align}f(g(2))&=f(0)\\&=3\cdot(0)+1\\&=1\end{align}$$

Notice that the process was exactly the same in both of the examples above. Specifically, we took the output of $g$ on some given input (such as $x=1$ or $2$) and fed it into the outer function $f$ as input. Note that the same process could be applied to any other input. Because of this, we can simplify the process a bit so we don’t do as much repeated work.

Alternate Approach (Useful if you need to compute the same thing repeatedly)

Notice that the expression $g(x)$ means “find the output of $g$ on input $x$ (whatever $x$ happens to be).” So, the expression $f(g(x))$ means “find the output of $g$ on input $x$ and plug it into $f$ as input” (just like the above examples, where $x=1,2$ specifically). Essentially, this is the more general version of what we did in the last two examples, but with a generic value for $x$, which we can replace with something specific later on if we want.

As such, the output of $g$ on input $x$ is given as $x^2-4$ (i.e. the rule tells you what the output is, based on what $x$ is). So, if we feed this output into $f$ as input, we get

$$\begin{align}f(g(x))&=f(x^2-4)\\&=3(x^2-4)+1\\&=3x^2-12+1\\&=3x^2-11\end{align}$$

Since $x$ was arbitrary in the above, the result $3x^2-11$ tells us how to compute (or what we’d get) if we plugged a specific $x$-value into $f(g(x))$. That is, we have built a rule for $f(g(x))$.

Thus, to compute $f(g(1))$ and $f(g(2))$, all we need to do is plug $x=1$ and $x=2$ into this new rule directly, since we know that $f(g(x))=3x^2-11$. Hence,

$$f(g(1))=3(1)^2-11=-8$$

and

$$f(g(2))=3(2)^2-11=1$$

Done.

Computing a rule first is certainly useful when you need to compute the output value of some combination of functions on some specific input value.

Notation

Let $f$ and $g$ be functions. We occasionally write $(f\circ g)(x)$ to mean $f(g(x))$.

Note that the notation for composition of functions differs slightly from multiplication, which is written $(f\cdot g)(x)$. Multiplication has a closed dot, and composition is more of an open circle.

$(f\circ g)(1)=48$

$(g\circ f)(2)=9$

$(f\circ h)(x)=3(x^2-1)^2-3(x^2-1)+2$

$(f(h(1))=2$

$f(h(2))=20$

$g(h(x))=(\sqrt{x})^3-(\sqrt{x})^2+1$

$h(g(x))=\sqrt{x^3-x^2+1}$

$f(g(1))$ Does Not Exist

$g(f(1))=0$

$(f\circ g\circ h)(x)=\frac{1}{\sqrt{x^2+1}}$

$(g\circ h\circ f)(x)=\sqrt{\frac{1}{x^2}+1}$

Previous Lesson

Back to Lesson

Next Topic

Precalculus Algebra

Composing Two Function Rules

Composing Functions Defined by Algebraic Rules

Evaluating Function Composition of Functions Defined by Rules

Function Composition with Numerical Initial \(x\)-Value Input

Alternate Approach (Useful if you need to compute the same thing repeatedly)

Notation