$Project Greater Ed Logo$

Circuits

Discrete Mathematics Paths and Circuits Circuits

Basics of Circuits

The following definitions are the “circuit” or “cycle” analogue of the definitions related to paths that we covered in previous topics.

Closed Walk

Let $G$ be a graph. A closed walk is a walk that starts and ends at the same vertex.

Note that a closed walk can have repeat edges and repeat vertices. See the following example

The following definitions place a few more restrictions on our closed walks.

Circuit and Simple Circuit

Let $G$ be a graph. A circuit is a closed walk with no repeated edges. A simple circuit is a circuit that passes through each vertex no more than once (with the exception of the start/end vertex).

A circuit that contains no edges is called a trivial circuit.

The image below depicts a circuit (left) and a simple circuit (right).

INSERT IMAGE OF CIRCUIT AND SIMPLE CIRCUIT. list out sequences.

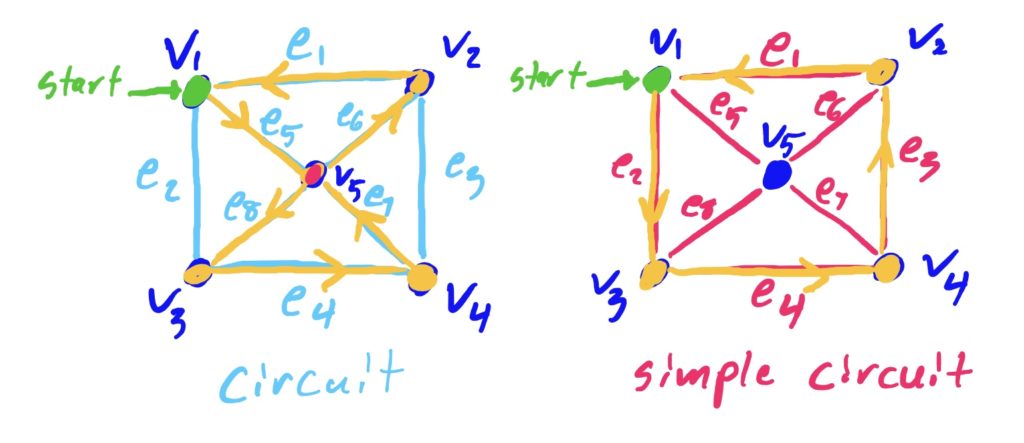
circuits can have repeated vertices. Simple circuits do not.

Useful Reference Table

	Repeated Edges Allowed?	Repeated Vertices Allowed?
Closed Walk	Yes	Yes
Circuit	No	Yes
Simple Circuit	No	No, except first/last

Euler Circuits

Recall that an Euler path is a path that passes through all edges in a connected graph $G$. Euler circuits are similar.

Euler Circuit

Let $G$ be a connected graph. An Euler circuit is a circuit that contains every edge in $E(G)$.

In other words, an Euler circuit is a path that passes through every single edge exactly once, returning where you started. The following image sequence illustrates an Euler path on graph depicted below.

Note that not every graph has an Euler circuit. And, even on the graphs that do have an Euler circuit, finding one is usually difficult, especially when dealing with graphs with a larger number of edges. As with all things, you get better with mindful practice.

A Useful Theorem

The following theorem is a Euler circuit analogue to the theorem that was presented with Euler paths.

Theorem

Let $G$ be a nonempty connected graph. $G$ has an Euler circuit if and only if the degree of each vertex is even.

The reason this is true, without giving a full proof, is because in order for a path to start and end at the same vertex without “reusing” edges, for every edge that we could leave a vertex by, there must be a different edge by which we “came into” that vertex. Thus every edge in the graph must be part of a pair at each vertex. If there were an edge that was not part of an “in/out” pair (i.e. a vertex had odd degree), then we would leave that vertex by that unpaired edge, never to return, or enter by that edge, never to leave. In either case, you cannot end where you started your path. This is illustrated below.

Note

The theorem above gives us an easy means by which we can determine whether a graph has an Euler circuit, but it does nothing to help us find one!

One possibility: $v_1e_2v_7e_5v_3e_{12}v_2e_3e_7v_6e_9v_3e_{12}v_2e-1v_1$. The edge $e_{12}$ is duplicated.

To have a closed path that is not a circuit, we need a duplicate edge in our closed path. The sequence above does that. Your answer may differ from mine.

$v_1e_2v_7e_7v_6e_9v_3e_5v_7e_3v_2e_1v_1$

Note that vertex $v_7$ is repeated, but we don’t have any repeated edges.

Do have a circuit that is not a simple circuit, we need to build a closed walk that has NO repeated edges, but has a repeated vertex aside from the initial vertex in the walk. The above answer does this. Your answer may differ.

It does not have an Euler circuit.

$v_1$ and $v_3$ have odd degree. The theorem covered in the lesson stated that the only way (if and only if) that a graph has an Euler circuit it if the degree of every vertex is even.

Any closed walk starting at $v_1$ will work.

Every vertex has even degree. So, all that’s left is to find the Euler circuit. In most cases, you can start at any vertex in a graph to draw your circuit, but it is easiest to see how the circuit is formed in the graph above if you start at vertex $v_1$.

Previous Topic

Back to Lesson

Next Lesson