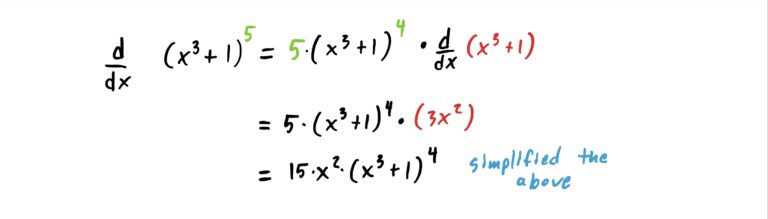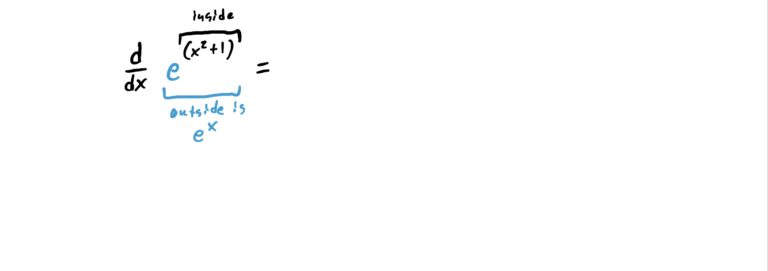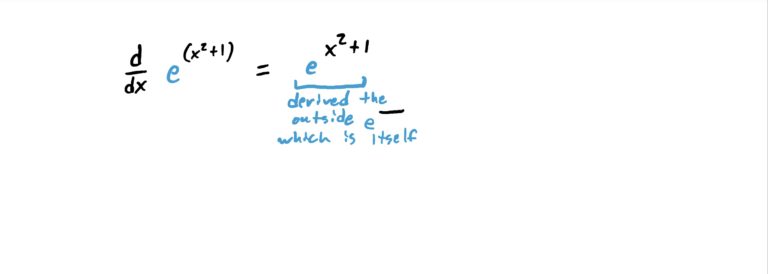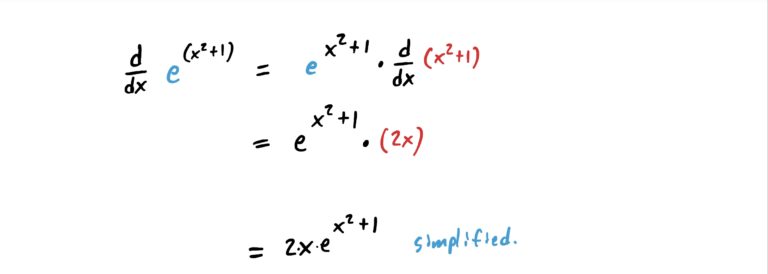Chain Rule
Deriving Composed Functions
So far, we’ve developed methods for deriving products of functions \(f(x)\cdot g(x)\), and quotients of functions \(\frac{f(x)}{g(x)}\). How do we go about deriving functions that are composed? That is, functions of the form \(f(g(x))\) where we are plugging one function into another?
Basically, what this rule is saying is “to find the derivative of \(f(g(x))\), find the derivative of the outside function, leaving the inside alone, and multiply by the derivative of the inside function.”
This rule makes short work of functions like \((x^2+1)^7\), or \(\sqrt{x^3+2x+1}\), or even logs and exponentials like \(\ln(x^2+1)\) and \(e^{3x^4-5x}\), respectively.
Notice first that we are dealing with function composition, where \(x^3+1\) is being “plugged into: \(x^5\). That is, \(x^3+1\) is “inside” the \(5\)th power function. So, to use the method of the chain rule, we “derive the outside, leave the inside alone, and multiply by the derivative of the inside function.” This is exhibited in the steps below.
Deriving Nasty Exponential Functions
We can use the chain rule to derive exponential functions such as \(e^{x^2+1}\) where the “inside function” is what you see in the exponent (because \(e^{x^2+1}\) is \(x^2+1\) “plugged into \(e^x\)). See how this works in the example below.
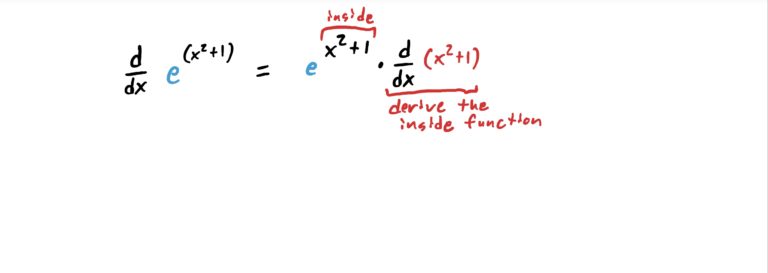
Notice that \(x^2+1\) is a function that is being “plugged into” the function \(e^x\). So, the “outside function” is the \(e^x\) and the “inside function” is \(x^2+1\). So, we derive \(H\) as shown in the steps below.
In other words, to derive an exponential function with something complicated in the exponent and \(e\) as the base, copy-paste the original function, then multiply by the derivative of the exponent. It’s that easy!
Use the chain rule to find the following derivatives.
Outside Function: \((—–)^3\)
\(\frac{d}{dx}f(g(x))=f'((g(x))\cdot g'(x)\)
Derive the Outside Function, Leave the inside function alone, then multiply by the derivative of the inside function
\(3(3x+2)^2\cdot 3\)
Outside Function: \((—–)^2\)
\(\frac{d}{dx}f(g(x))=f'((g(x))\cdot g'(x)\)
Derive the Outside Function, Leave the inside function alone, then multiply by the derivative of the inside function
\(2(2x-1)\cdot 4\) or \(8x-4\) (simplified)
Outside Function: \(5\cdot(——)^{20}\)
\(\frac{d}{dx}f(g(x))=f'((g(x))\cdot g'(x)\)
Derive the Outside Function, Leave the inside function alone, then multiply by the derivative of the inside function
\(100\cdot (x^2+x+1)^19\cdot (2x+1)\)
Outside Function is \(e^x\), Inside is \(2x+1\)
\(\frac{d}{dx} e^{g(x)}=e^{g(x)}\cdot g'(x)\)
Derive the outside function (i.e. the exponential \(e^{(——)}\), which is itself, copy-pasted), then multiply by the derivative of the inside function (i.e. the exponent)
\(2e^{2x+1}\)
Outside Function is \(e^x\), Inside is \(x^2+2x+1\)
\(\frac{d}{dx} e^{g(x)}=e^{g(x)}\cdot g'(x)\)
Derive the outside function (i.e. the exponential \(e^{(——)}\), which is itself, copy-pasted), then multiply by the derivative of the inside function (i.e. the exponent)
\(e^{x^2+2x+1}\cdot (2x+2)\)
First convert radical to a fractional power, then outside function is \((——-)^{\frac{1}{2}}\)
Derive the Outside Function, Leave the inside function alone, then multiply by the derivative of the inside function
\(\frac{d}{dx}f(g(x))=f'((g(x))\cdot g'(x)\)
\((4+2x)^{-\frac{1}{2}}\) or \(\frac{1}{(4+2x)^{\frac{1}{2}}}\)
First convert radical to a fractional power, then inside function is \(1+x^2+4x^3\)
Derive the Outside Function, Leave the inside function alone, then multiply by the derivative of the inside function
\(\frac{d}{dx}f(g(x))=f'((g(x))\cdot g'(x)\)
\(\frac{1}{4}(1+x^2+4x^3)^{-\frac{3}{4}}\cdot(2x+12x^2)\) or \(\frac{2x+12x^2}{4\cdot(1+x^2+4x^3)^{\frac{3}{4}}}\)
Outside Function is \(e^x\), Inside is \(\sqrt{x}+x^2\). Convert radicals to fractional powers before taking derivatives.
Derive the Outside Function, Leave the inside function alone, then multiply by the derivative of the inside function
\(\frac{d}{dx} e^{g(x)}=e^{g(x)}\cdot g'(x)\)
\(e^{\sqrt{x}+x^2}\cdot (\frac{1}{2x^{1/2}}+2x)\)
Outside Function is \(e^x\), Inside is \(\sqrt[3]{x}+\sqrt{x}\). Convert radicals to fractional powers before anything else.
Derive the Outside Function, Leave the inside function alone, then multiply by the derivative of the inside function
\(\frac{d}{dx} e^{g(x)}=e^{g(x)}\cdot g'(x)\)
\(e^{\sqrt[3]{x}+\sqrt{x}}\cdot (\frac{1}{3x^{2/3}}+\frac{1}{2x^{1/2}})\)
Outside Function: \((——)^{-\frac{1}{2}}\)
Derive the Outside Function, Leave the inside function alone, then multiply by the derivative of the inside function
\(\frac{d}{dx}f(g(x))=f'((g(x))\cdot g'(x)\)
\(\frac{-4x}{(1+4x^2)^{\frac{3}{2}}}\)
First bring denominator up to numerator and make the exponent negative. Then, outside function is \(5\cdot(—-)^{30}\)
Derive the Outside Function, Leave the inside function alone, then multiply by the derivative of the inside function
\(\frac{d}{dx}f(g(x))=f'((g(x))\cdot g'(x)\)
\(-300x\cdot(x^2+1)^{-31}\) or \(\frac{-300x}{(x^2+1)^{31}}\)
First bring the denominator up to the numerator, and make exponent negative.
Derive the Outside Function, Leave the inside function alone, then multiply by the derivative of the inside function
\(\frac{d}{dx}f(g(x))=f'((g(x))\cdot g'(x)\)
\(\frac{-\pi}{6\cdot x^{\frac{1}{2}}\cdot (x^{\frac{1}{2}}-1)^{\frac{4}{3}}}\) or \(\frac{-\pi}{6\cdot \sqrt{x}\cdot (\sqrt{x}-1)^{\frac{4}{3}}}\)
First, convert radical to fractional power in the denominator, then bring the whole denominator up to numerator, making the exponent negative.
Derive the Outside Function, Leave the inside function alone, then multiply by the derivative of the inside function
\(\frac{d}{dx}f(g(x))=f'((g(x))\cdot g'(x)\)
\(-2x^3\cdot(1+x^4)^{\frac{-5}{4}}\) or \(\frac{-2x^3}{(1+x^4)^{\frac{5}{4}}}\)