$Project Greater Ed Logo$

Areas Between Curves

Business Calculus Area, Continuous Accumulation, and Definite Integrals Areas Between Curves

Finding Areas Between Curves

We at times are interested in determining the area between two curves defined on an interval. This is depicted below. This sort of situation arises when one wants to find differences between totals of quantities that continuously vary.

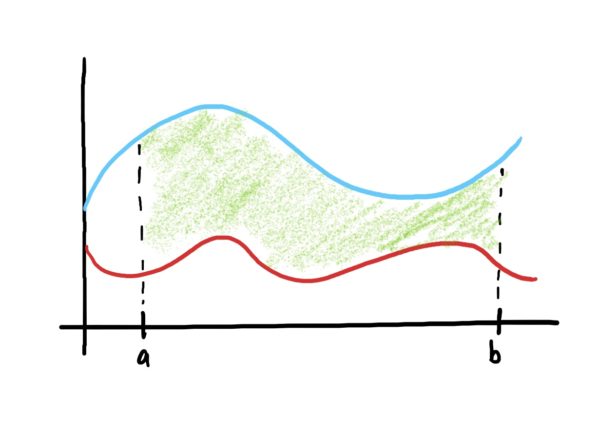
two graphs defined on an interval with the area between them shaded

Thankfully, finding the area between two curves is easy!

Finding Areas Between Two Curves on an Interval

Suppose we have continuous functions \(f\) and \(g\) that do not intersect on an interval \([a,b]\). Also, assume that \(f(x)\geq g(x)\) for all \(x\) in \([a,b]\) (i.e. \(f\) is the “top” function). Then the area between \(f\) and \(g\) on interval \([a,b]\) is given by
$$\int^b_a f(x)-g(x)\ dx$$
or
$$\int^b_a f(x)\ dx – \int^b_ag(x)\ dx$$
(whichever you prefer; they’re equivalent).

If you look at the second formula above, the first integral gives you the area under the top function \(f\), and the second gives you the area under \(g\). We are subtracting the integrals because in order to find the area between the two curves, we are effectively subtracting the area of \(g\) away from the area under \(f\) (because the area under \(g\) is contained in the area under \(f\)). This idea is depicted in the image sequence below.

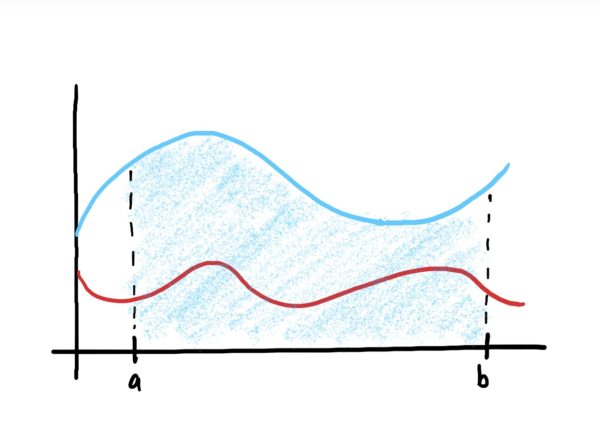
two graphs shown, with blue one above and the area underneath it shaded

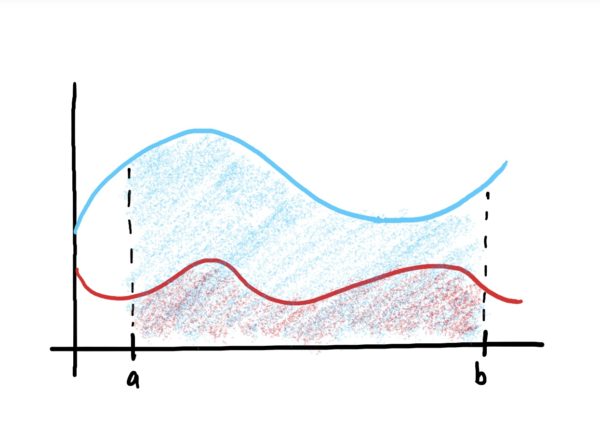
same two graphs shown, but with the lower function's area shaded underneath it, overlapping the area from the higher function

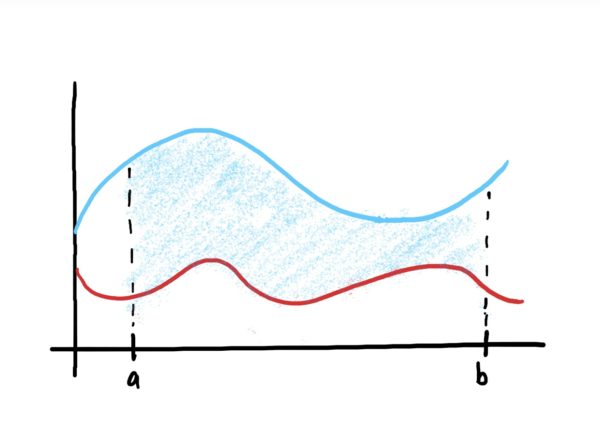
both functions drawn again, with the lower function's area removed from the higher function's area

Note that the first formula is nothing more than a combination of the two integrals into a single integral using the additive property for antiderivatives/integrals.

Determining the Top Function

More often than not, we are not given the graphs of the two functions whose graphs we want to find the area between. As such, in order to use the formula above, we need to determine which function is the “top” function. This is easy, assuming that your functions don’t cross: Simply take your favorite \(x\)-value on the given interval and plug it into both functions. Whichever one produces the higher \(y\)-value is the top function (because we are assuming the graphs don’t cross at all, which would change which function is “on top.”) Try some of the examples below, seeing if you can solve a few of them without anything but the formula above and the method for determining the “top” function just described.

Subtract the lower function from the higher, then integrate the result.

Area between \(f\) and \(g\) on \([a,b]\) = \(\int^b_a f(x)-g(x)\ dx\) where the top function is \(f\), in this case.

Computing areas between two curves on an interval:

Given functions \(f,g\), determine which function is the “top” function. Either:
- Graph the two functions and pick the top
- plug an \(x\)-value between \(a\) and \(b\) into both functions. Whichever has a bigger \(y\)-value is the top function. (NOTE: we are running under the assumption that the graphs don’t cross on \([a,b]\))
Subtract the bottom function from the top; maybe simplify.
Integrate

Area\(=\frac{8}{3}\)

Subtract the lower function from the higher, then integrate the result.

Area between \(f\) and \(g\) on \([a,b]\) = \(\int^b_a f(x)-g(x)\ dx\) where the top function is \(f\), in this case.

Computing areas between two curves on an interval:

Given functions \(f,g\), determine which function is the “top” function. Either:
- Graph the two functions and pick the top
- plug an \(x\)-value between \(a\) and \(b\) into both functions. Whichever has a bigger \(y\)-value is the top function. (NOTE: we are running under the assumption that the graphs don’t cross on \([a,b]\))
Subtract the bottom function from the top; maybe simplify.
Integrate

Area\(=6\)

Subtract the lower function from the higher, then integrate the result.

Area between \(f\) and \(g\) on \([a,b]\) = \(\int^b_a f(x)-g(x)\ dx\) where the top function is \(f\), in this case.

Computing areas between two curves on an interval:

Given functions \(f,g\), determine which function is the “top” function. Either:
- Graph the two functions and pick the top
- plug an \(x\)-value between \(a\) and \(b\) into both functions. Whichever has a bigger \(y\)-value is the top function. (NOTE: we are running under the assumption that the graphs don’t cross on \([a,b]\))
Subtract the bottom function from the top; maybe simplify.
Integrate

Area\(=\frac{1}{4}\)

Subtract the lower function from the higher, then integrate the result.

Area between \(f\) and \(g\) on \([a,b]\) = \(\int^b_a f(x)-g(x)\ dx\) where the top function is \(f\), in this case.

Computing areas between two curves on an interval:

Given functions \(f,g\), determine which function is the “top” function. Either:
- Graph the two functions and pick the top
- plug an \(x\)-value between \(a\) and \(b\) into both functions. Whichever has a bigger \(y\)-value is the top function. (NOTE: we are running under the assumption that the graphs don’t cross on \([a,b]\))
Subtract the bottom function from the top; maybe simplify.
Integrate

Area\(=\frac{5}{8}-\ln\left \vert \frac{1}{2} \right\vert \)

Subtract the lower function from the higher, then integrate the result.

Area between \(f\) and \(g\) on \([a,b]\) = \(\int^b_a f(x)-g(x)\ dx\) where the top function is \(f\), in this case.

Computing areas between two curves on an interval:

Given functions \(f,g\), determine which function is the “top” function. Either:
- Graph the two functions and pick the top
- plug an \(x\)-value between \(a\) and \(b\) into both functions. Whichever has a bigger \(y\)-value is the top function. (NOTE: we are running under the assumption that the graphs don’t cross on \([a,b]\))
Subtract the bottom function from the top; maybe simplify.
Integrate

Area\(=\frac{4}{3}\)

Subtract the lower function from the higher, then integrate the result.

Area between \(f\) and \(g\) on \([a,b]\) = \(\int^b_a f(x)-g(x)\ dx\) where the top function is \(f\), in this case.

Computing areas between two curves on an interval:

Given functions \(f,g\), determine which function is the “top” function. Either:
- Graph the two functions and pick the top
- plug an \(x\)-value between \(a\) and \(b\) into both functions. Whichever has a bigger \(y\)-value is the top function. (NOTE: we are running under the assumption that the graphs don’t cross on \([a,b]\))
Subtract the bottom function from the top; maybe simplify.
Integrate

Area\(=\frac{1}[6}\)

Subtract the lower function from the higher, then integrate the result.

Area between \(f\) and \(g\) on \([a,b]\) = \(\int^b_a f(x)-g(x)\ dx\) where the top function is \(f\), in this case.

Computing areas between two curves on an interval:

Given functions \(f,g\), determine which function is the “top” function. Either:
- Graph the two functions and pick the top
- plug an \(x\)-value between \(a\) and \(b\) into both functions. Whichever has a bigger \(y\)-value is the top function. (NOTE: we are running under the assumption that the graphs don’t cross on \([a,b]\))
Subtract the bottom function from the top; maybe simplify.
Integrate

Area\(=\frac{8}{3}\)

Subtract the lower function from the higher, then integrate the result.

Area between \(f\) and \(g\) on \([a,b]\) = \(\int^b_a f(x)-g(x)\ dx\) where the top function is \(f\), in this case.

Computing areas between two curves on an interval:

Given functions \(f,g\), determine which function is the “top” function. Either:
- Graph the two functions and pick the top
- plug an \(x\)-value between \(a\) and \(b\) into both functions. Whichever has a bigger \(y\)-value is the top function. (NOTE: we are running under the assumption that the graphs don’t cross on \([a,b]\))
Subtract the bottom function from the top; maybe simplify.
Integrate

Area\(=8\)