$Project Greater Ed Logo$

Antiderivatives that Result in Logarithms

Business Calculus The U-Substitution Method Antiderivatives that Result in Logarithms

Recall How Deriving Logs Works

Suppose we want to find the derivative of the function $f(x)=\ln(x^3+4)$. To do this, we need to employ the chain rule because we have a function inside another function: $x^3+4$ is being plugged into the logarithm $\ln(x)$. The result of deriving this is below:

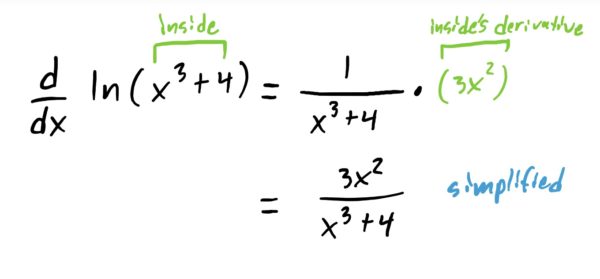
Notice that, in the final answer of the derivative performed above that the derivative of the denominator is what you see in the numerator. This is somewhat of a “signature feature” of derivatives of logarithms. When trying to find antiderivatives of fractions that have this feature, we thus know that the result will be a logarithm. Of course, we can carry out the process of antideriving using u-sub.

Antideriving these special fractions…

Suppose we want to compute

$$\int \frac{7x^6+2x+1}{x^7+x^2+x-6}\ dx$$

Notice first that the numerator is exactly the derivative of the denominator. Since we are trying to find a function that has this fraction as it’s derivative, and based on what we observed in the previous section, we know that this indefinite integral will be a logarithm with the denominator inside.

If we want to carry out this antiderivative using u-substitution, we can simply let the denominator of the fraction be our “inside function” and call it $u$. Then, computing $\frac{du}{dx}$ the substitution is very natural. See below for how this works out.

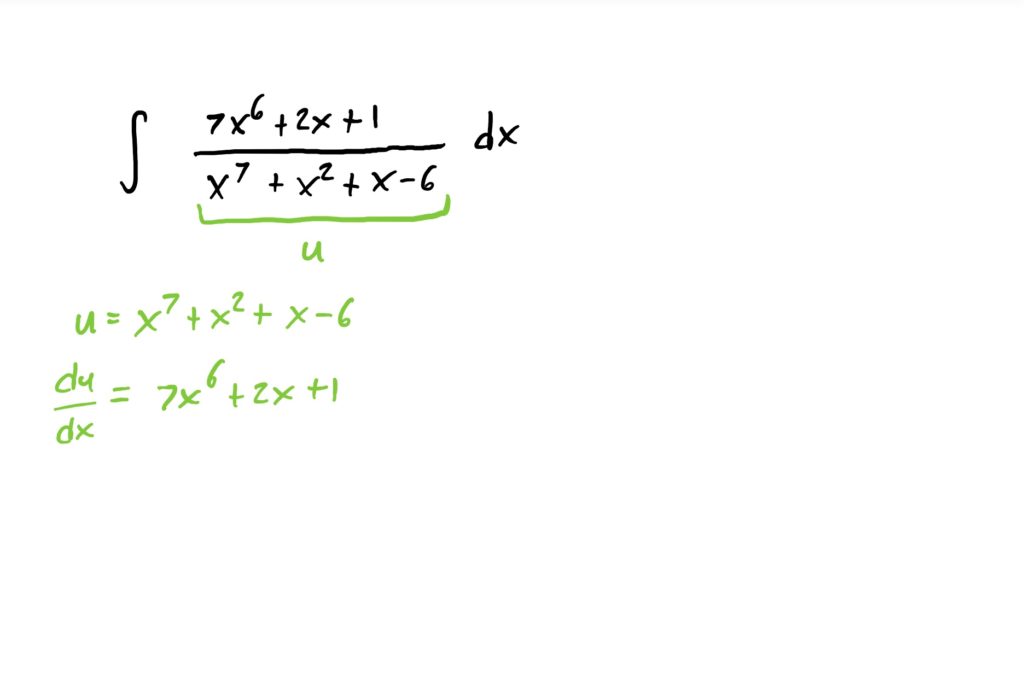
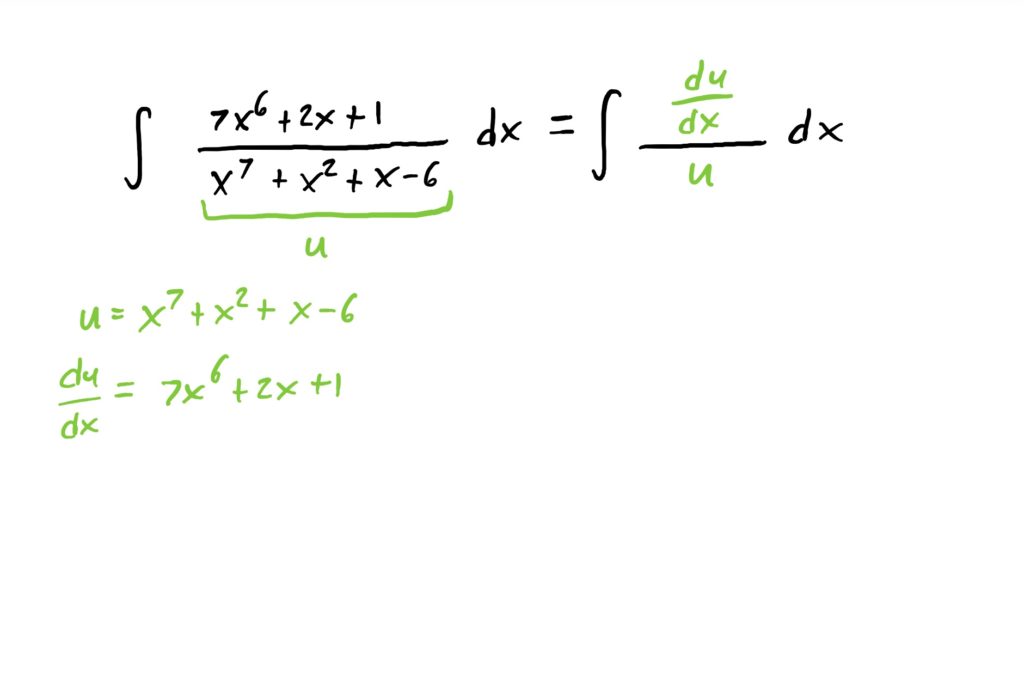
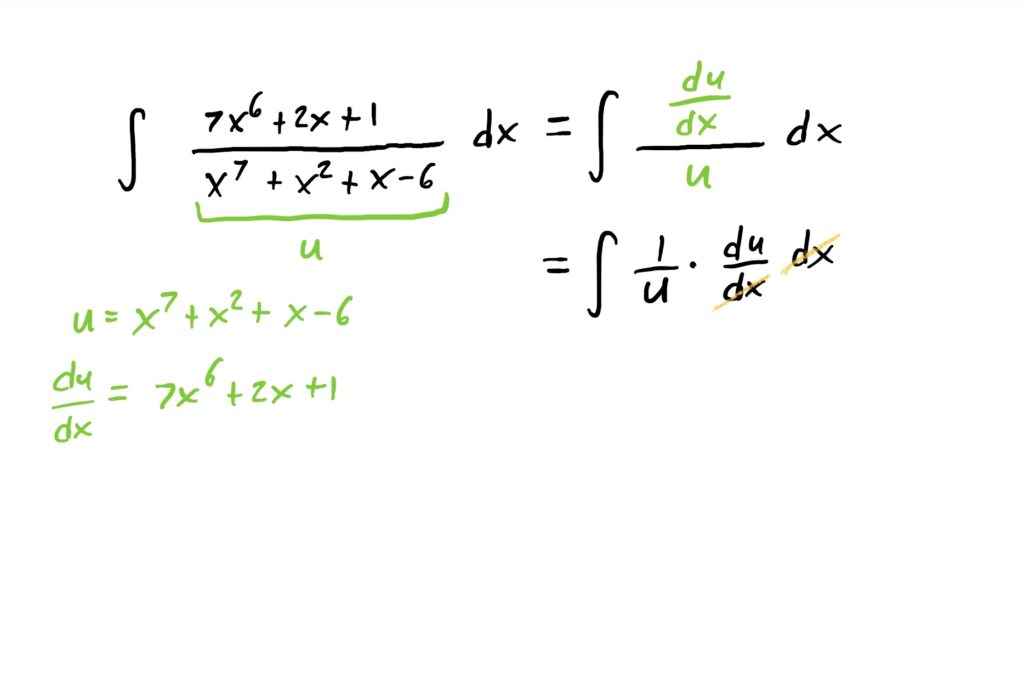
carrying out the substitution so you have u in the denominator and du/dx in the numerator

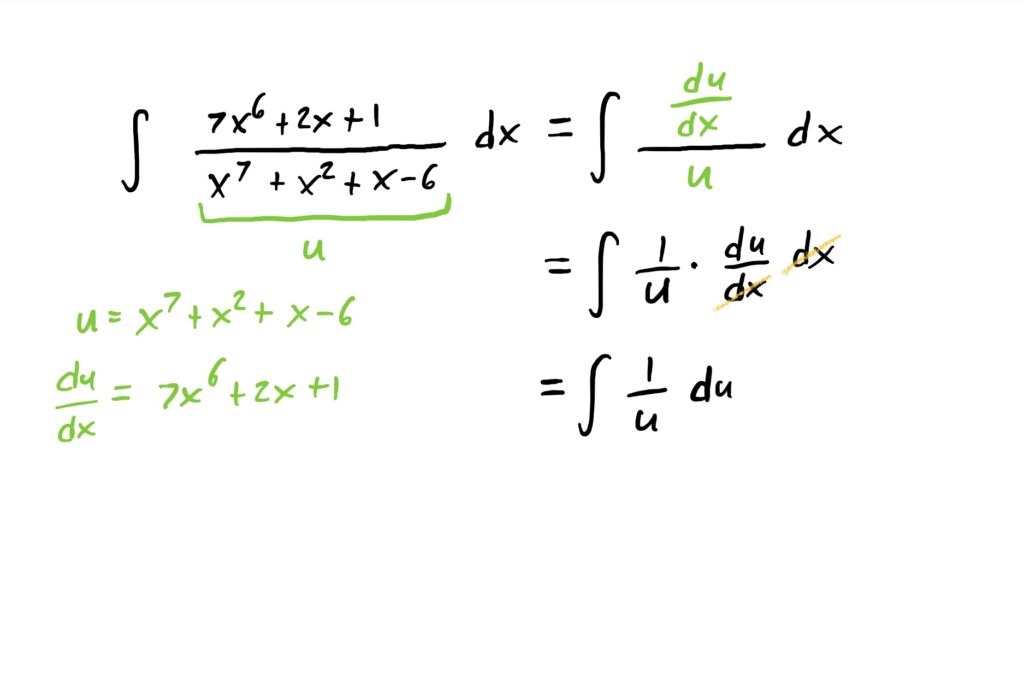
simplifying so that you now have an integral entirely in terms of u

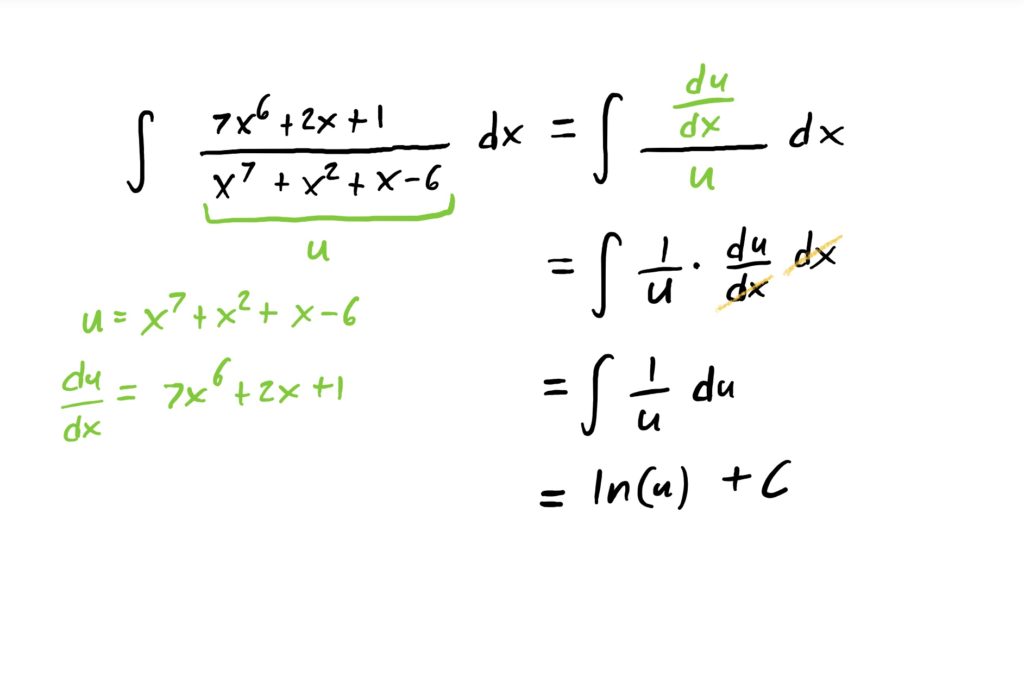
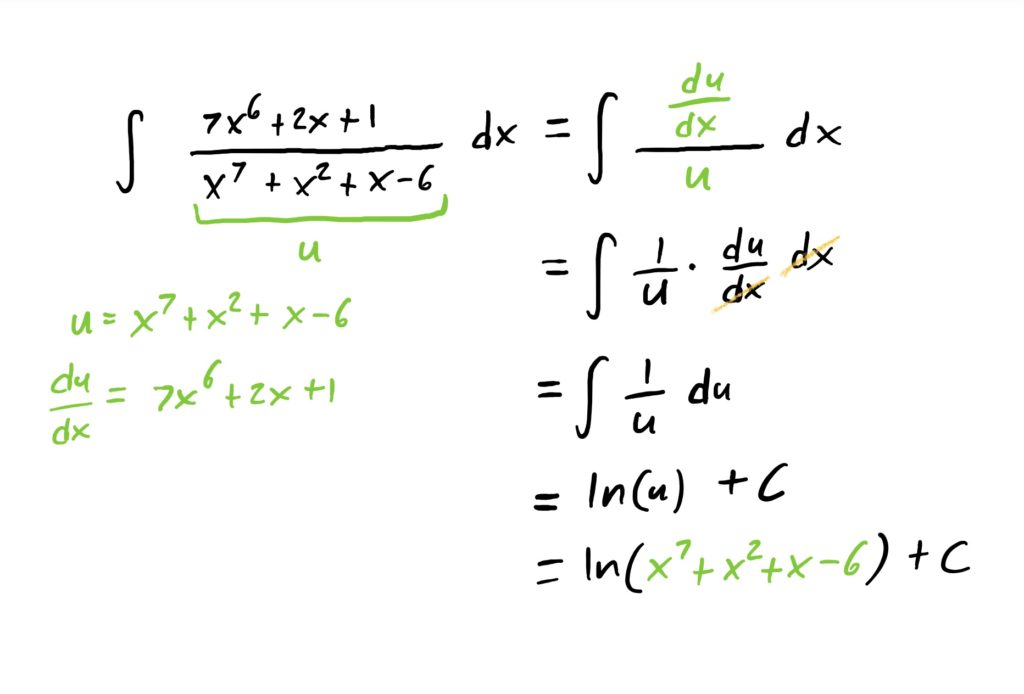
It should be noted that at times the numerator of these fractions is not exactly like the derivative of the denominator. If this happens, you might need to rearrange the $\frac{du}{dx}$ equation or event the $u$ equation so that wehn you carry out the substitution, there will be no more $x$-stuff remaining, leaving only an integral in terms of $u$ to be computed.

Compute the following antiderivatives

Let $u=x+1$.

First find an “inside function” and let it be called $u$.
Find the derivative of $u$, $\frac{du}{dx}$
Find where the expressions you have for $u$ and $\frac{du}{dx}$ appear in the integral and replace them in the integrand with $u$ and $\frac{du}{dx}$. You may need to first rearrange the equations for $u$ or $\frac{du}{dx}$ before substituting. Your integral should have no $x$’s anymore after subbing.
integrate as usual. Don’t forget “+C”
plug back in your $u$ formula and call it a day
(If computing a definite integral, then plug in upper and lower limits in for $x$, and subtract the results.)

$\ln\vert x+1 \vert+C$

Let $u=x^2+1$

First find an “inside function” and let it be called $u$.
Find the derivative of $u$, $\frac{du}{dx}$
Find where the expressions you have for $u$ and $\frac{du}{dx}$ appear in the integral and replace them in the integrand with $u$ and $\frac{du}{dx}$. You may need to first rearrange the equations for $u$ or $\frac{du}{dx}$ before substituting. Your integral should have no $x$’s anymore after subbing.
integrate as usual. Don’t forget “+C”
plug back in your $u$ formula and call it a day
(If computing a definite integral, then plug in upper and lower limits in for $x$, and subtract the results.)

$\ln\vert x^2+1 \vert +C$

Let $u=\ln(x^2+1)$. Yes. Including the Log.

First find an “inside function” and let it be called $u$.
Find the derivative of $u$, $\frac{du}{dx}$
Find where the expressions you have for $u$ and $\frac{du}{dx}$ appear in the integral and replace them in the integrand with $u$ and $\frac{du}{dx}$. You may need to first rearrange the equations for $u$ or $\frac{du}{dx}$ before substituting. Your integral should have no $x$’s anymore after subbing.
integrate as usual. Don’t forget “+C”
plug back in your $u$ formula and call it a day
(If computing a definite integral, then plug in upper and lower limits in for $x$, and subtract the results.)

$\frac{\ln(x^2+1)^2}{4}+C$

Let $u=\ln(x)$

First find an “inside function” and let it be called $u$.
Find the derivative of $u$, $\frac{du}{dx}$
Find where the expressions you have for $u$ and $\frac{du}{dx}$ appear in the integral and replace them in the integrand with $u$ and $\frac{du}{dx}$. You may need to first rearrange the equations for $u$ or $\frac{du}{dx}$ before substituting. Your integral should have no $x$’s anymore after subbing.
integrate as usual. Don’t forget “+C”
plug back in your $u$ formula and call it a day
(If computing a definite integral, then plug in upper and lower limits in for $x$, and subtract the results.)

$\ln\vert \ln \vert x \vert \vert +C$

Let $u=\ln(\sqrt{t})$

First find an “inside function” and let it be called $u$.
Find the derivative of $u$, $\frac{du}{dx}$
Find where the expressions you have for $u$ and $\frac{du}{dx}$ appear in the integral and replace them in the integrand with $u$ and $\frac{du}{dx}$. You may need to first rearrange the equations for $u$ or $\frac{du}{dx}$ before substituting. Your integral should have no $x$’s anymore after subbing.
integrate as usual. Don’t forget “+C”
plug back in your $u$ formula and call it a day
(If computing a definite integral, then plug in upper and lower limits in for $x$, and subtract the results.)

$(\ln(\sqrt{t}))^2+C$

Let the denominator be your $u$… or you can simplify the integrand to make your life real easy.

First find an “inside function” and let it be called $u$.
Find the derivative of $u$, $\frac{du}{dx}$
Find where the expressions you have for $u$ and $\frac{du}{dx}$ appear in the integral and replace them in the integrand with $u$ and $\frac{du}{dx}$. You may need to first rearrange the equations for $u$ or $\frac{du}{dx}$ before substituting. Your integral should have no $x$’s anymore after subbing.
integrate as usual. Don’t forget “+C”
plug back in your $u$ formula and call it a day
(If computing a definite integral, then plug in upper and lower limits in for $x$, and subtract the results.)

$\frac{1}{6} \ln \vert (2x+1)^3 \vert +C$

Previous Topic

Back to Lesson

Next Lesson