$Project Greater Ed Logo$

Algebraically Solving Equations

Business Calculus Solving Equations with Functions Algebraically Solving Equations

Getting $x$ “By Itself”

In addition to the other methods for solving equations that we’ve discussed so far, the most familiar to most people is that of “solving for $x$” algebraically. There are many methods for doing this depending on what’s happening inside the equation. Usually we are able to directly “solve for $x$” by getting $x$ by itself on one side of the equation. The idea is that if you are given an equation and asked to solve for a specific variable, you effectively “undo” the algebraic operations (such as addition, subtraction, multiplication, powers, roots, etc.) that are “happening to” $x$ in order to get $x$ by itself on one side of the equation and a number on the other side of the equation, telling you what $x$ must be. We give several examples of this below as a review as most of this is covered in a typical precalculus course.

Solving Linear Equations

The goal of this problem (as with all these problems) is to get $x$ by itself on one side of the equation so that there is a number on the other side. The idea is to first get all $x$-stuff to one side of the equation, and everything else to the other side using algebra. Whatever you do to one side of the equation must be done to the other side as well so the equation always “balances out.” The steps for this are shown below.

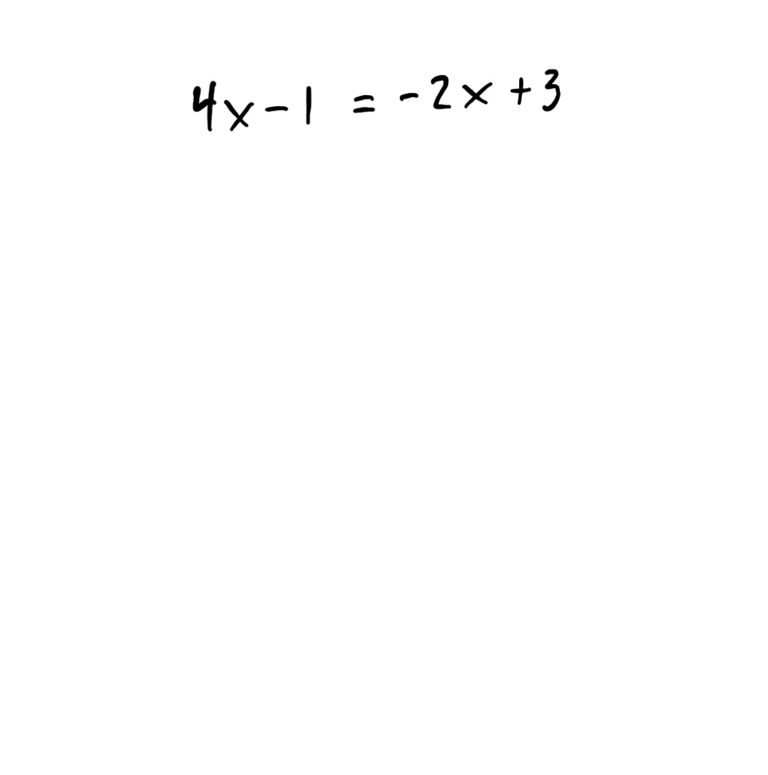
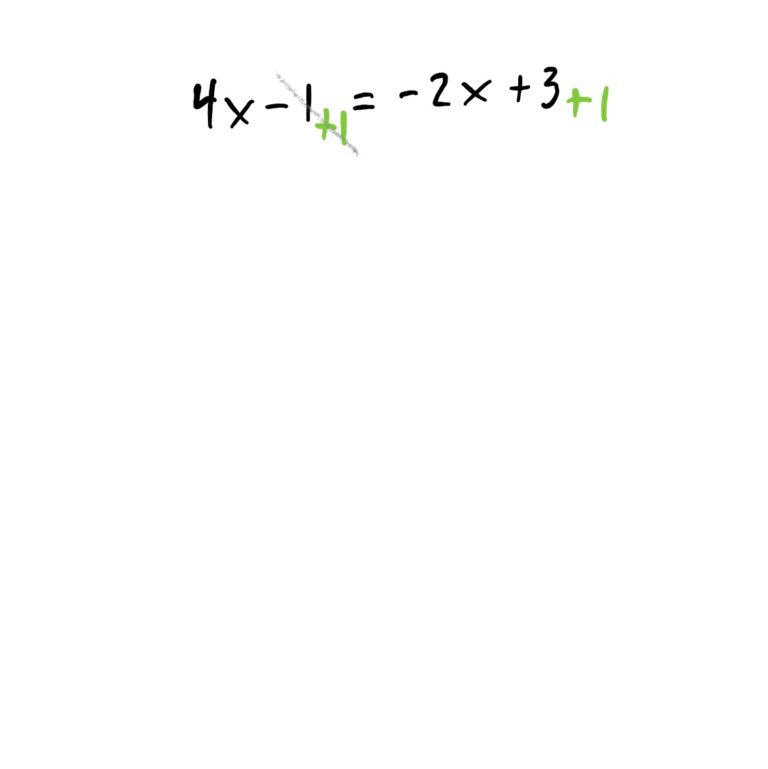
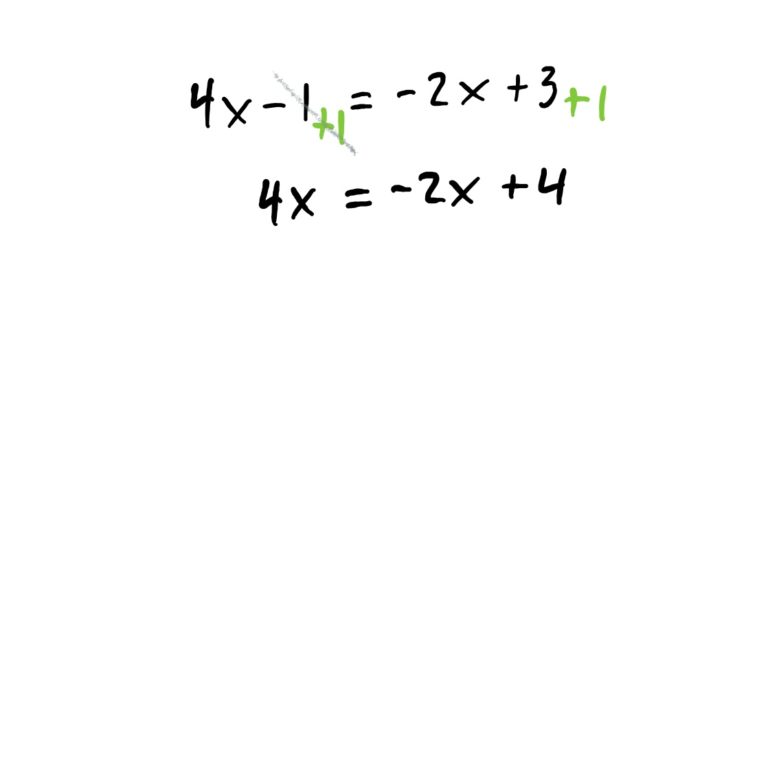
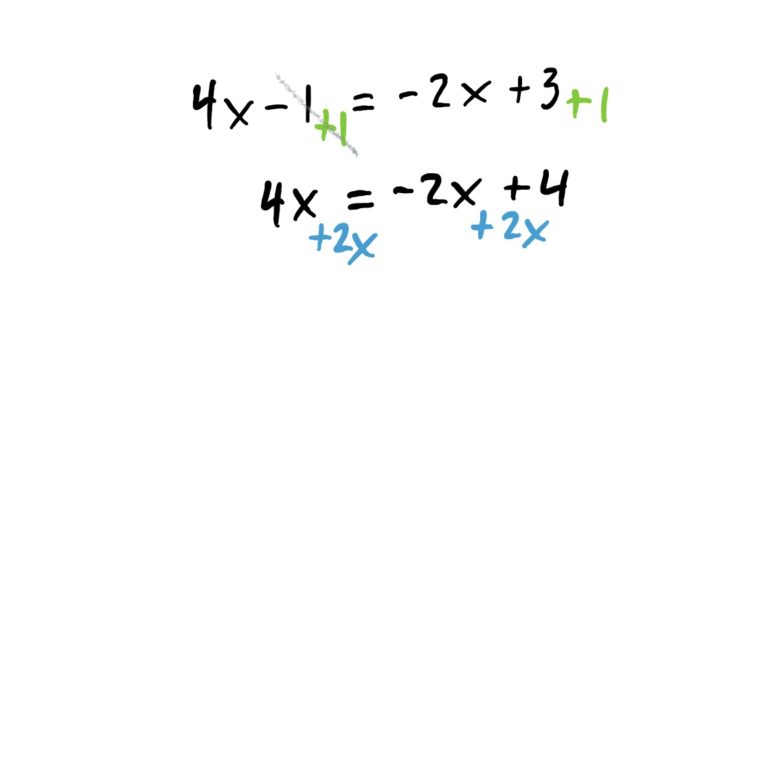
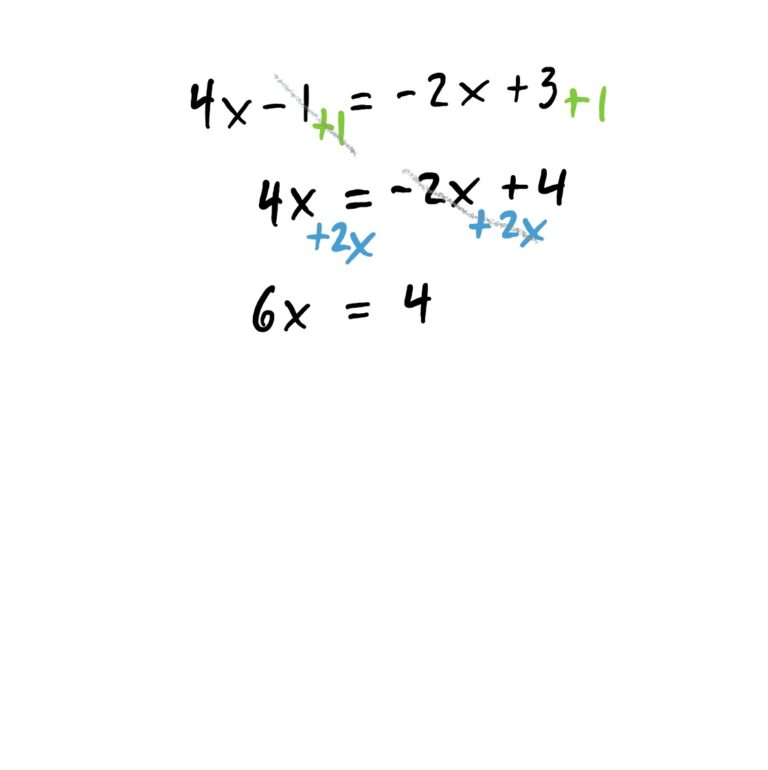
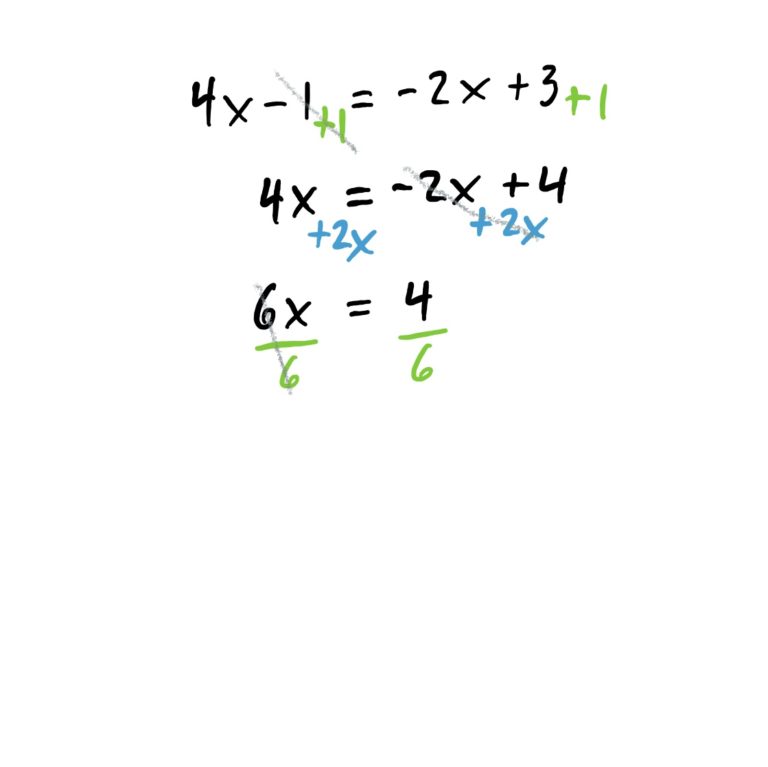
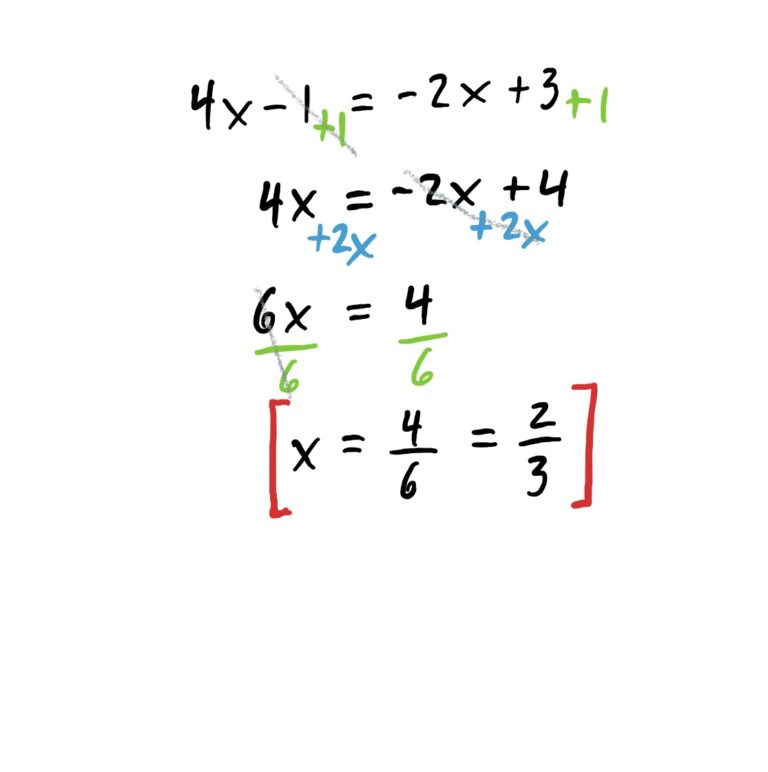
Need to review solving linear equations?

Check out the lesson on solving linear equations in the Precalculus Algebra eText.

Cancelling powers to get $x$ by itself

Recall that one can cancel powers using radicals of the same power. This is summarized in the following power-cancellation law.

Power Cancellation Law

Let $n$ be a positive whole number. Then:
If $n$ is odd, then $\sqrt{n}(x^n)=(\sqrt{n}(x))^n=x$
If $n$ is even, then $\sqrt{n}(x^n)=(\sqrt{n}(x))^n=|x|$

That is, when cancelling an odd power with the “same power” odd root, you get just $x$. However, when $n$ is even, you end up with absolute values around $x$. When it comes to solving equations and the even-power, even-root cancellation, this results in needing a “plus or minus,” effectively giving you two possible solutions to your equation. This is explained in the example below.

There is a lot happening around $x$ in this equation. Start by undoing the operations from the outside in. This is demonstrated in the steps below.

square root both sides to cancel the power 2

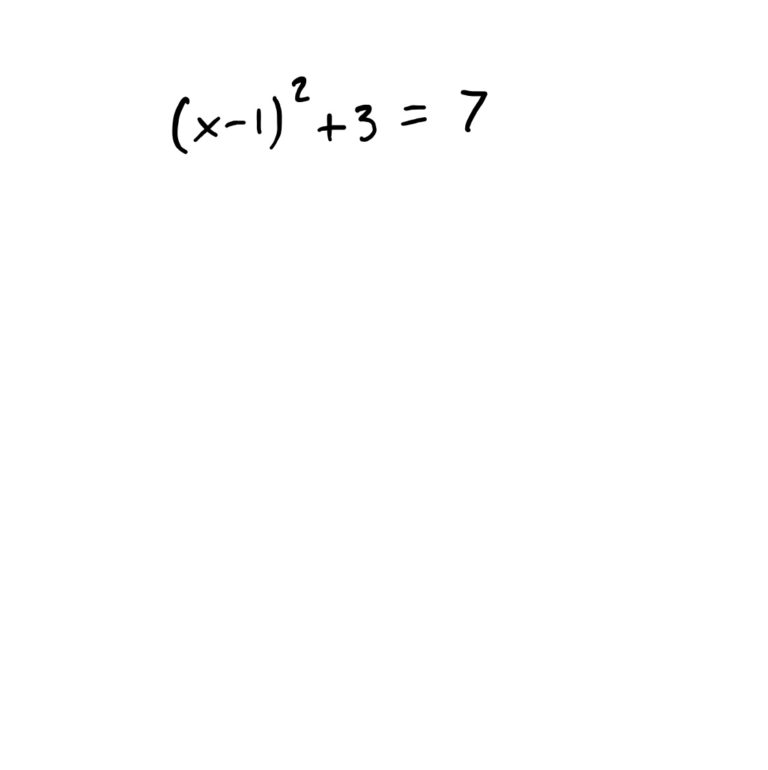
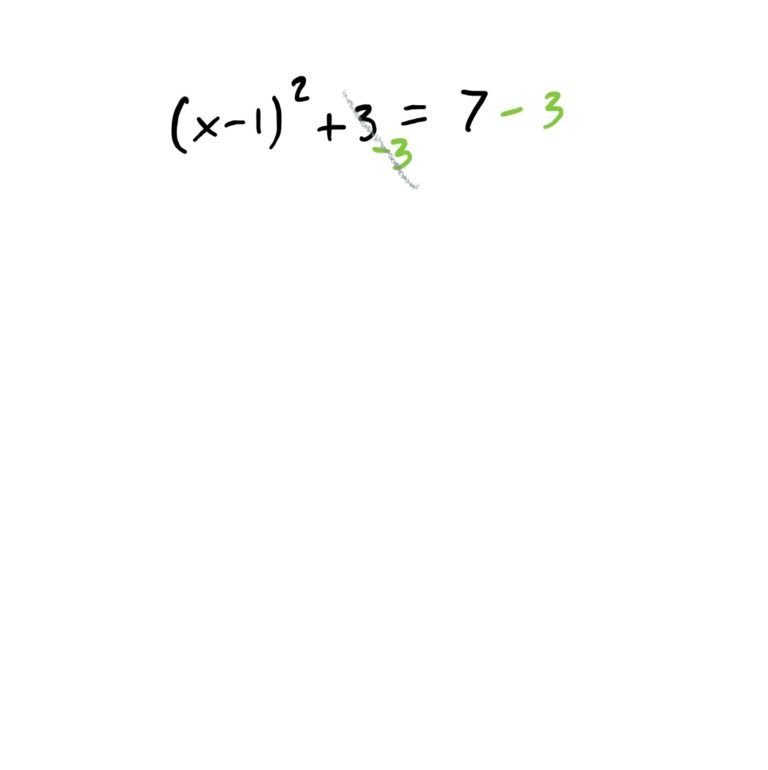
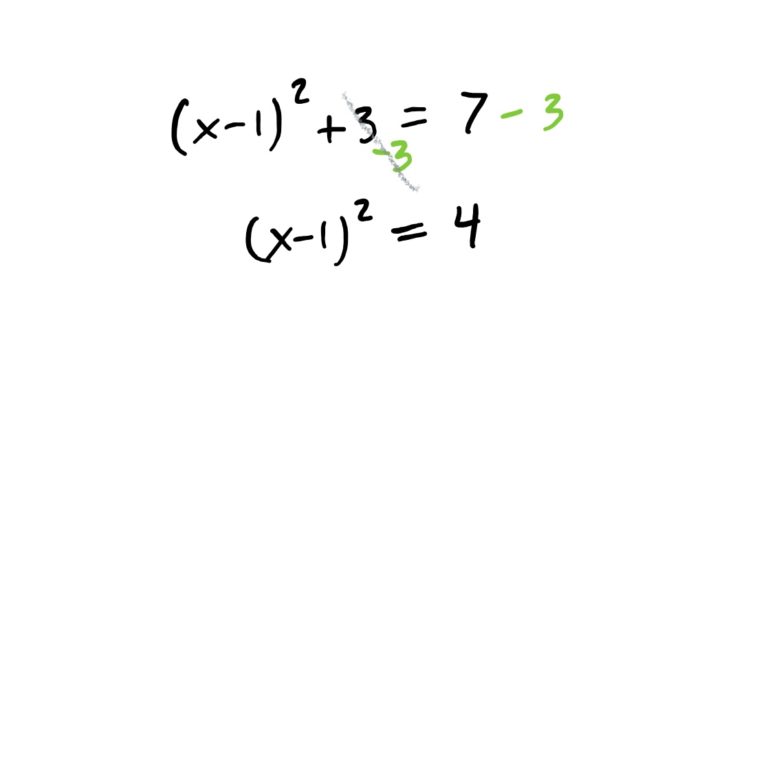
result, with absolute value on the left-hand-side

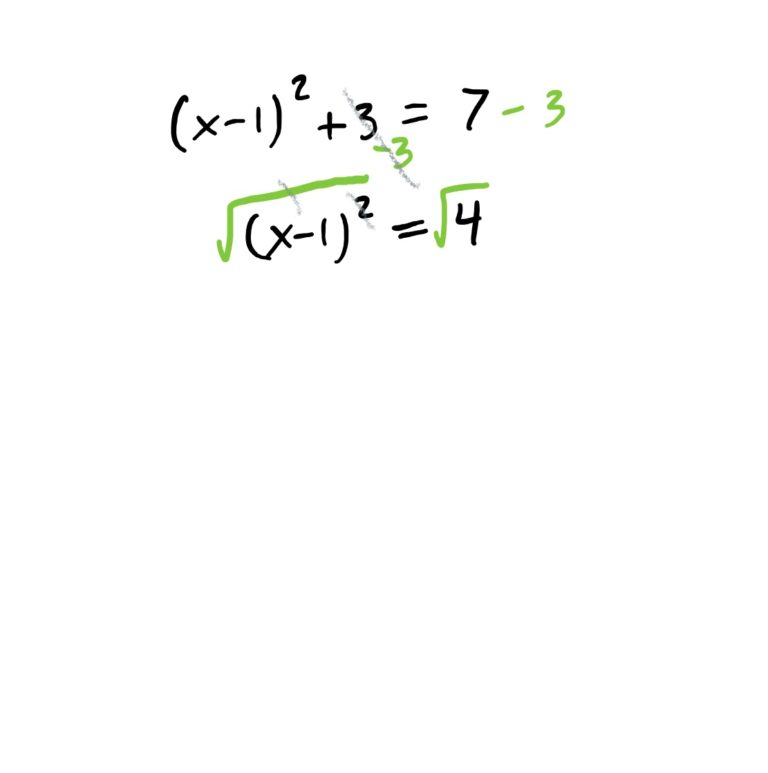
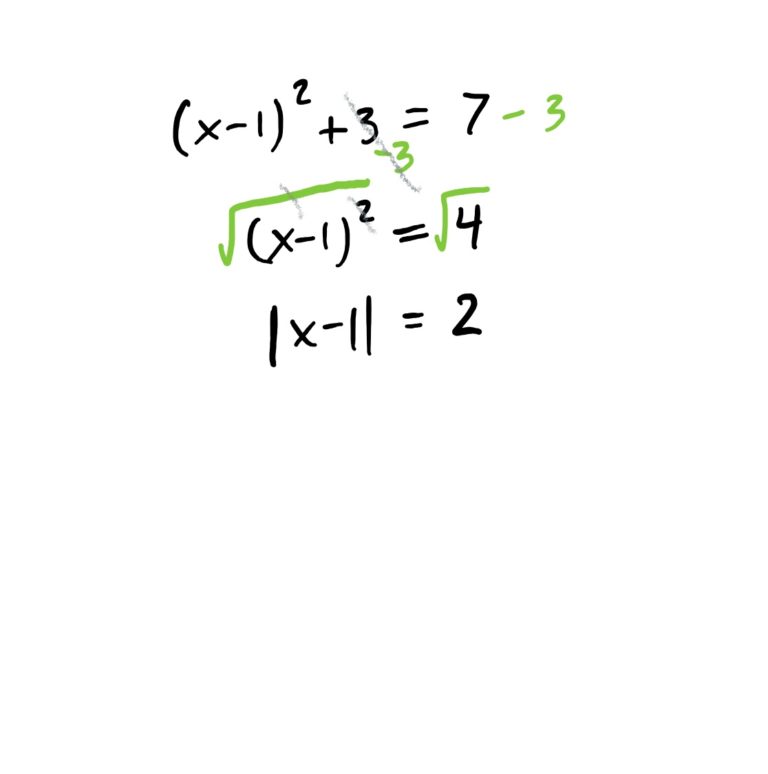
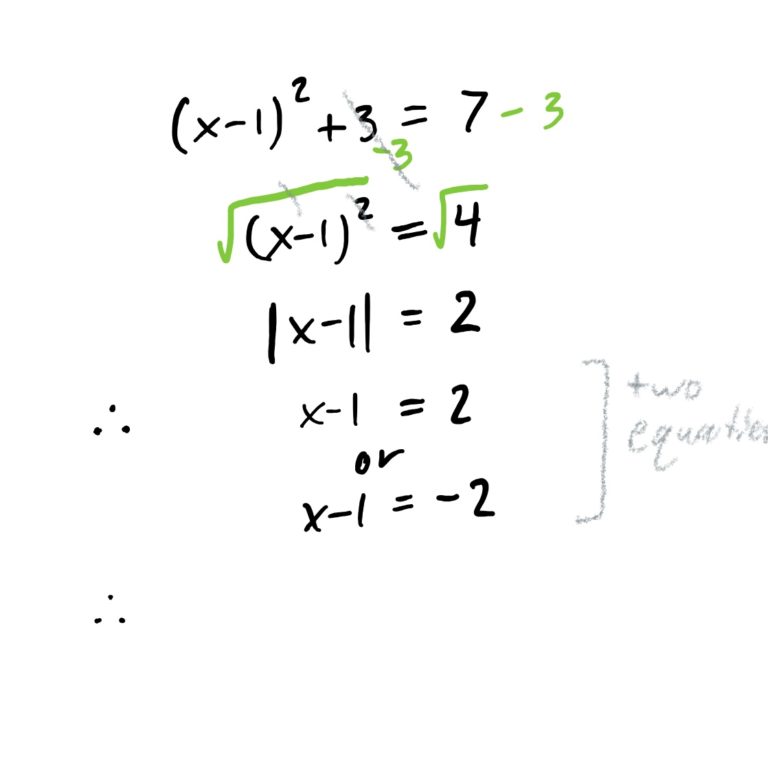
turns into two separate equations because of the absolute value

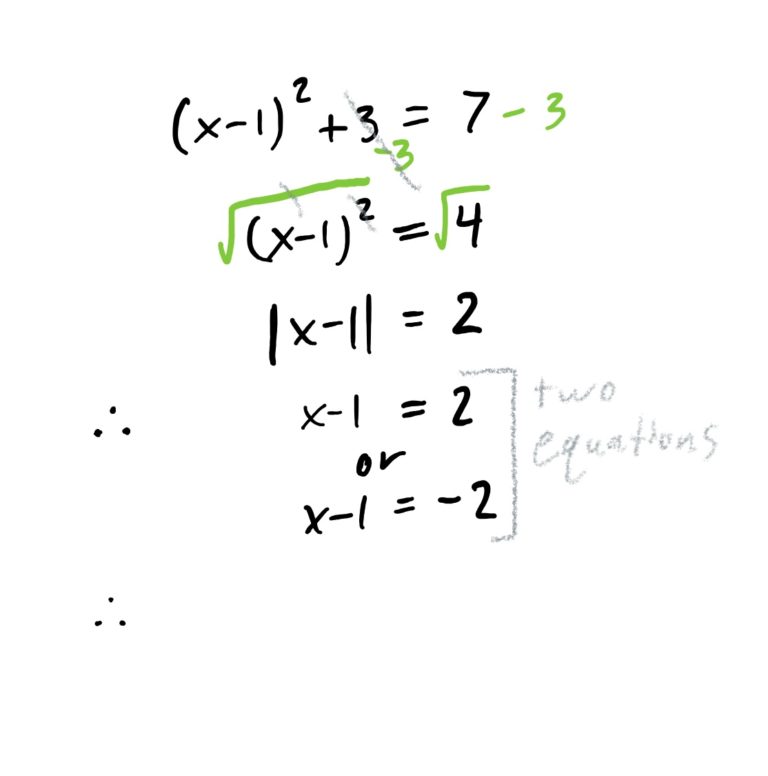
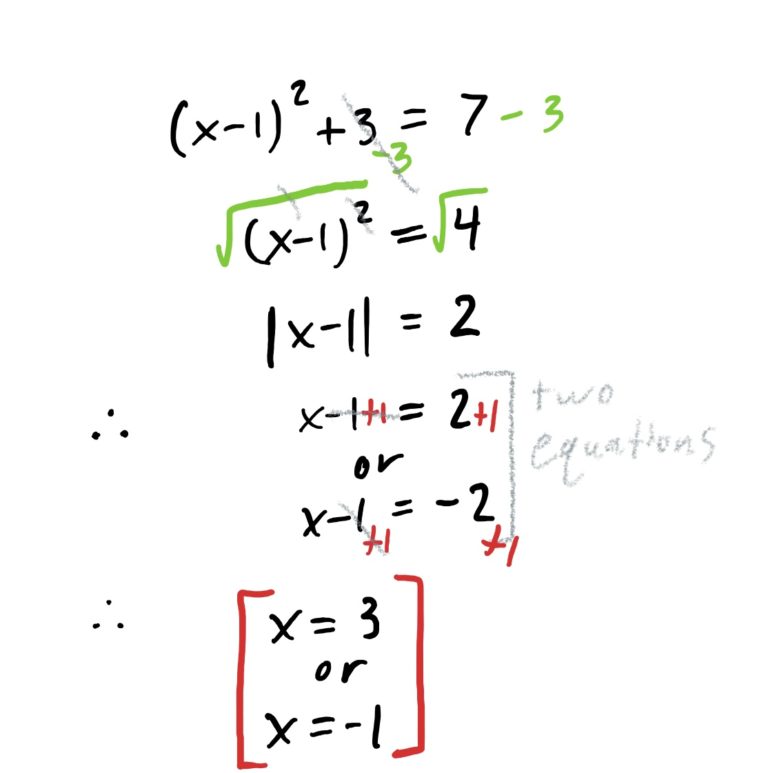
Recall that absolute values means “make the number inside the absolute values positive (once you have a single number inside them).” When we see the equation $|x-1|=2$, this is saying that “the absolute value of $x-1$ must be $2$,” so therefore, the only way this is possible is if $x-1$ is equal to $2$ or $-2$, because if $x-1$ is one of these two things, the absolute value will be 2.

REMEMBER! Absolute values (or just plus or minus, if you want to skip that step) are only needed when you are cancelling an even power with an even root. For ODD root/power cancellation, you do NOT need absolute values or a plus or minus.

Uglier Quadratics

Often in we are not given quadratic equations that are so nice to solve, such as the one found above. Normally, we have ones given like the one in the following example. For these, we need to use the Quadratic Formula (or factor things, if it is immediately clear how to do so).

Quadratic Formula

Suppose you are given a quadratic equation like $ax^2+bx+c=0$ where $a\neq 0$, $b$ and $c$ are all real numbers. Then, the solutions to this equation are given by the formula
$$x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$$

Solving quadratic equations requires little more than plugging your coefficients $a,b$ and $c$ into this formula, and carefully computing the result. As before, the “$\pm$” gives you two solutions to the equation.

First thing we need to do is get the equation to have a $0$ on one side. This can be done by adding $2$ to both sides, cancelling the $-2$ on the RHS. Then, we can plug everything into the quadratic formula and compute the result. All this is shown below.

the original equation with 0 on one side

writing down the quadratic formula before plugging in everything

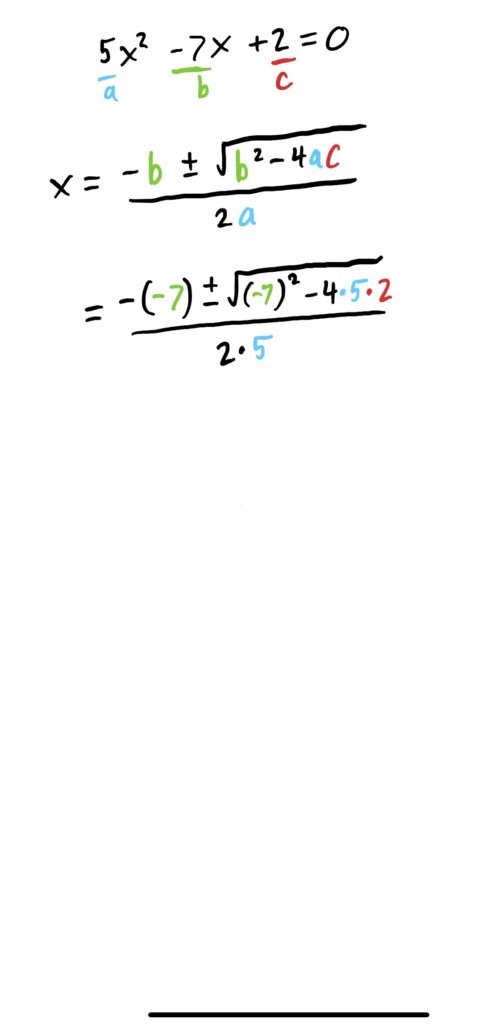
plugging everything into the quadratic formula

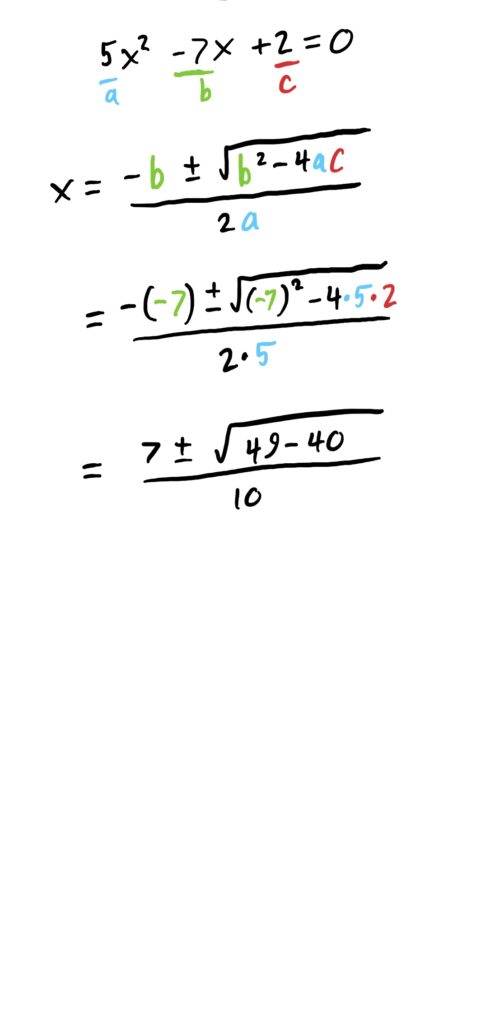
simplifying computations inside the radical and before the plus or minus

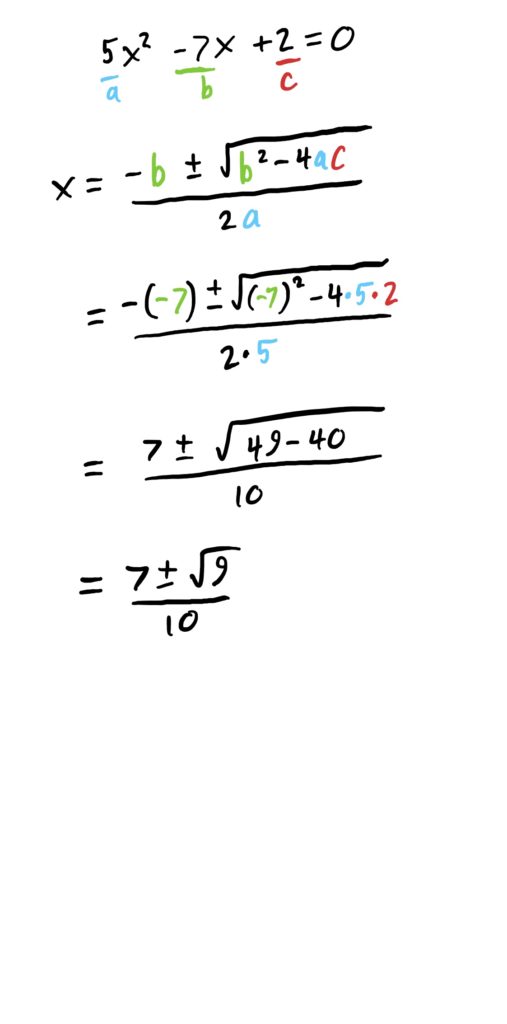
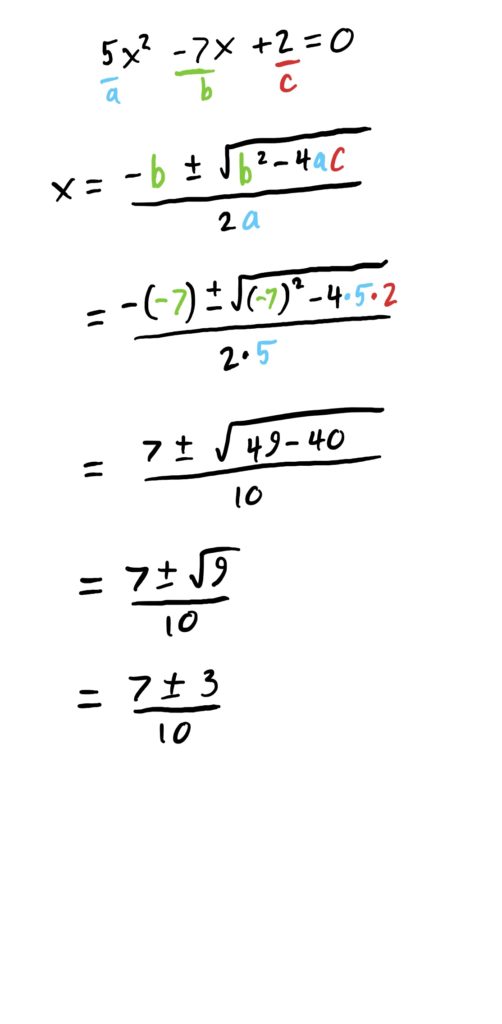
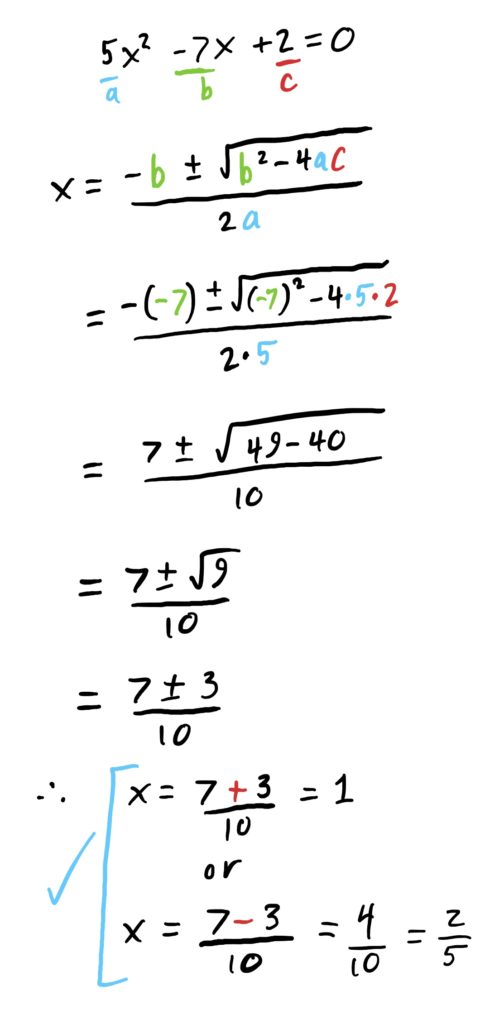
left with two equations, one for the plus and one for the minus.

When solutions don’t exist

When solving quadratic equations (or any equation, really) algebraically. If you ever find yourself taking the the square root of a negative number, you know that no real-number solutions exist.

You might have learned about imaginary or complex numbers and that you can get solutions to equations with the imaginary unit $i$ in them. Those are complex number solutions and are not real numbers. They come from mathematicians essentially forcing $sqrt{-1}$ to have an answer when it normally doesn’t (can’t take square roots of negative numbers). Complex numbers are very useful and have a medley of applications, but they are beyond the scope of this eText.

Need Additional Review of Quadratic Equations?

Check out the lesson on solving quadratic equations from the Precalculus eText!

Solving Exponential Equations

Exponential equations are equations that have exponential expressions in them, such as $3\cdot 2^{x-1}=4$. We can solve these equations by first rearranging the equation to get a simple exponential function on one side of the equation, and then take logarithms on both sides to cancel the base to isolate the exponent. This is summarized in the rule below.

Log-Exponential Cancellation Property (part 1)

If $a>0$ and if $x$ is a real number, then
$$\log_a(a^x)=x$$

That is, taking logs of exponential expressions of the same base results in cancellation of the base of the log AND the exponential expression, leaving you with just what was in the exponent. Let’s see how we can use this principle to solve exponential equations.

See the process below! Again, the idea is to first get the exponential expression $5^{3x-1}$ by itself on one side of the equation, and then take the logarithm of both sides. This will isolate the $3x-1$ exponent on one side, all by itself. This makes the rest of the problem straightforward.

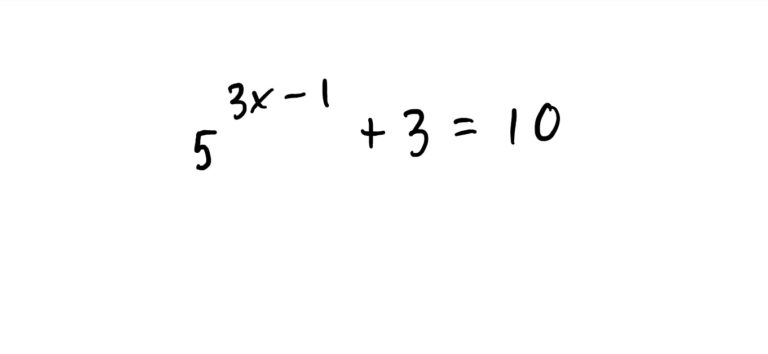
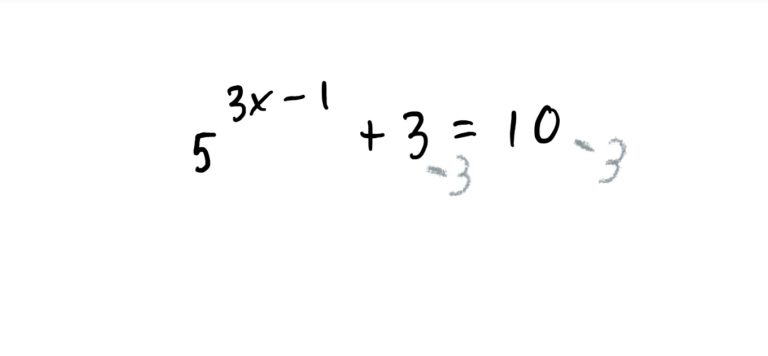
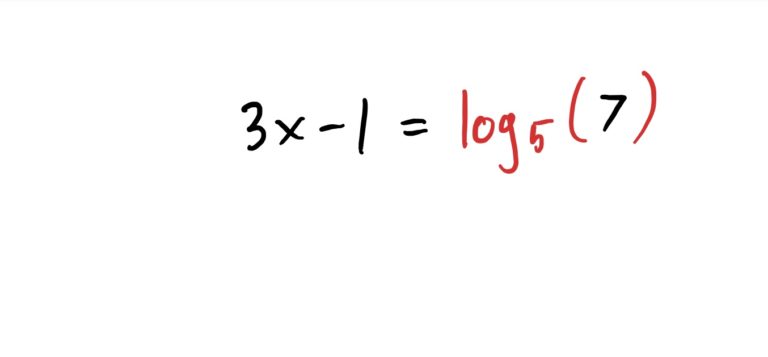
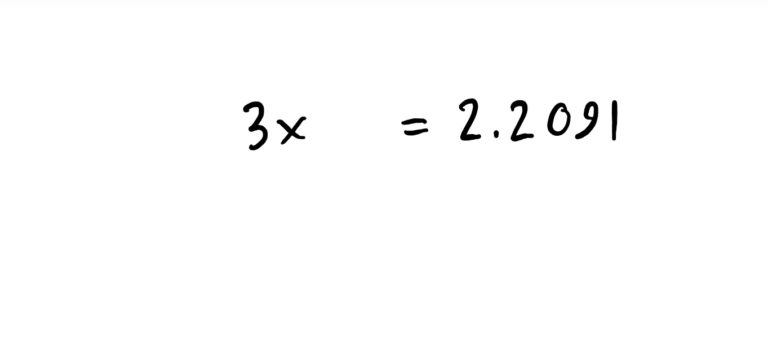
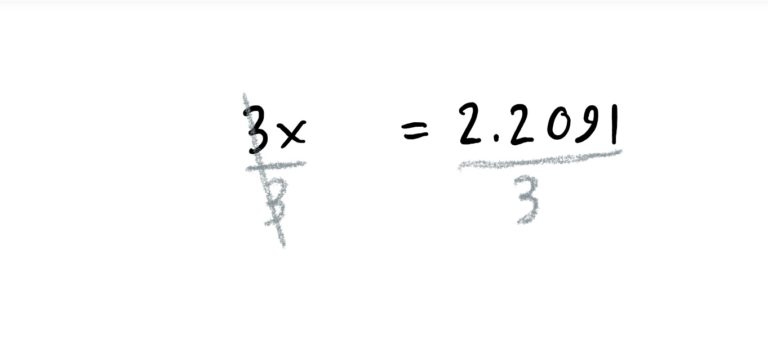
Some exponential equations are a little more involved and require the use of Log Laws.

Solving Logarithmic Equations

Just like one can have exponential equations, so too can one have logarithmic equations, or equations with logs in them. Solving these basically works the same way as exponential equations. We first try to get the log stuff all on one side of an equation, and then apply the following cancellation rule:

Log-Exponential Cancellation Property

If $a>0$ and if $x$ is a real number, then
$$a^{\log_a(x)}=x$$

This tells us that if we want to solve an equation with a log in it, after getting a log by itself, we can exponentiate both sides so that the base is the same as that of the log. Then, the base and the log cancel, giving you what was inside the log originally. This is shown in the following example.

See the process below! Again, the idea is to first get the log by itself on one side. We do this by adding 3 to both sides to get what you see below. Then, we apply that cancellation rule above, giving us a way to cancel the log. After that, the rest of the problem is easy. See the work below for how we do all this.

Need additional review on solving exponential or log equations?

To go to the Precalculus Algebra eText lesson on Logarithms, click here. Here you will find everything regarding logs, log laws, and solving log equations.

To specifically review solving logarithmic and exponential equations, click here.

Solve the following linear equations

Complete as many of these as you feel necessary to understand the overall concept.

Need to review solving linear equations?

Check out the lesson on solving linear equations in the Precalculus Algebra eText.

$x=\frac{5}{4}$

$x=1$

$x=\frac{3}{8}$

$x=8$

$x=-0.82174$

$x=\frac{3}{4}$

$x=\frac{10}{3}$

$x=3$

Solve the following equations with powers

Note that some of these problems might not have any solutions! Be careful!

Need Additional Review of Quadratic Equations and Powers?

Check out the lesson on solving quadratic equations from the Precalculus eText!

$x=\pm 1$

$x=2i$ or $x=-2i$

$x=\sqrt{3}+2$ or $x=-\sqrt{3}+2$

$x=-2$

$x=\sqrt{2}+1$ or $x=-\sqrt{2}+1$

$x=-\frac{3}{4}$

Solve the following quadratic equations

Need Additional Review of Quadratic Equations?

Check out the lesson on solving quadratic equations from the Precalculus eText!

$x=25.9369$ OR $x=0.4858577$

$x=0.35779$ or $x=0.0537488$

$x=-0.0616$ OR $x=-14.03697$

Solve the following exponential equations

Need additional review on solving exponential or log equations?

To go to the Precalculus Algebra eText lesson on Logarithms, click here. Here you will find everything regarding logs, log laws, and solving log equations.

To specifically review solving logarithmic and exponential equations, click here.

$\log_3(4)=1.2618595$

$\log_{\frac{1}{2}}(9)=-3.169925$

$\log_{0.4}(2)=-0.756471$

$\log_2\left(\frac{20}{3}\right)=2.73696559$

$\log_{1.7}\left(\frac{102}{3}\right)=6.64563$

$\log_{1.23}\left(\frac{16}{5}\right)=5.61870$

Solve the following logarithmic equations

Need additional review on solving exponential or log equations?

To go to the Precalculus Algebra eText lesson on Logarithms, click here. Here you will find everything regarding logs, log laws, and solving log equations.

To specifically review solving logarithmic and exponential equations, click here.

$x=e^2$