PRAXIS: Solving Functional Equations

1. Find an approximate solution to the equation \(x^3-5=-1\) using the guess and check method. Ensure \(x^3-5\) (on the Left-hand side) produces an output that is within \(0.1\) of \(-1\) (i.e. the Right-hand side) when this approximate \(x\)-value solution is plugged in.
2. Let \(f\) and \(g\) be defined using the graphs below. Find all approximate solutions to the equation \(f(x)=g(x)\).

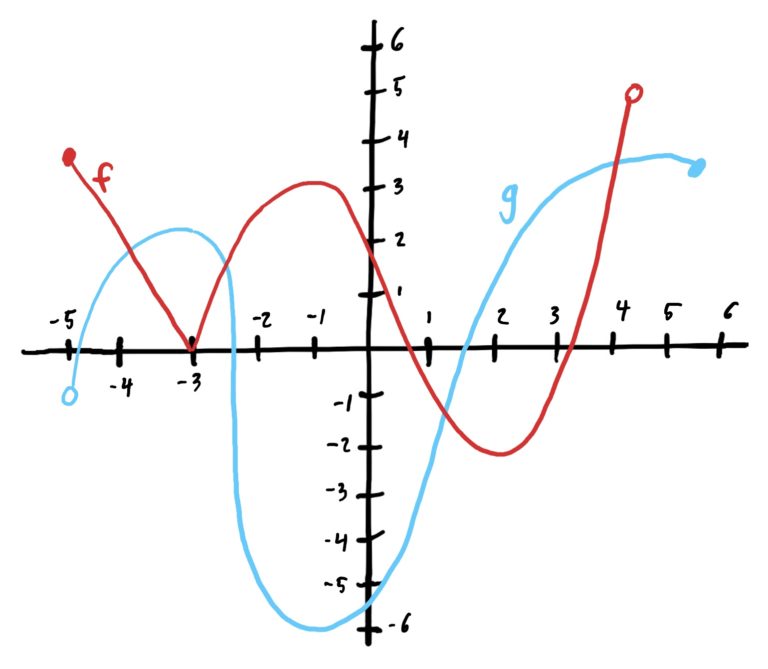
Solve each of the following equations for \(x\) using algebraic techniques.

3. \(4x+1=5(x+1)\)
4. \(4x^2-5=11\)
5. \(5.2x^2-4x+2=0\)
6. \(3.14x^2=7x+0.5\)
7. \(5x^3+7=5\)
8. \(\log_5(3x+1)=2\)
9. \(3^{3x+1}=3^{5x-2}\)
10. \(e^{7x^2+2.3x-9}=1\)