Your table must have at least 10 rows: 5 values less than $2$, and 5 values greater than $2$. The $x$-values must also approach $x=2$ as demonstrated in examples in the lesson(s).

Use a table to guess the limit

$$\lim_{x\rightarrow -1} \frac{x^2+2x+1}{x+1}$$

Your table must have at least 10 rows: 5 values less than $-1$ and 5 greater than $-1$, similar to what you did above.

Let $f$ be the function defined by the graph below

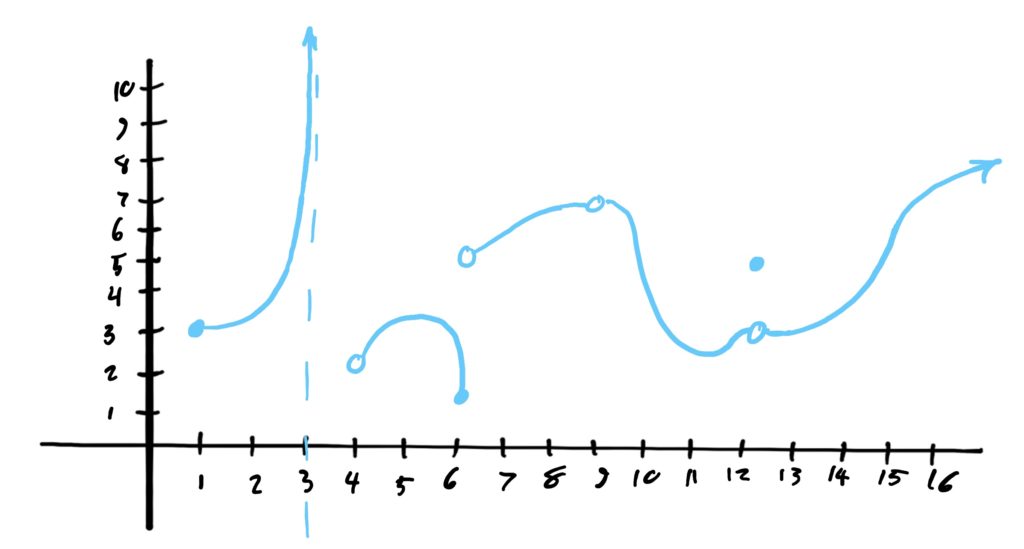
graph with an asymptote and several jumps

Find the following limits if they exist.

$\lim_{x\rightarrow 1^+} f(x)$
$\lim_{x\rightarrow 4^+} f(x)$
$\lim_{x\rightarrow 6} f(x)$
$\lim_{x\rightarrow 9} f(x)$
$\lim_{x\rightarrow 12} f(x)$
$\lim_{x\rightarrow 15} f(x)$

Find the following limits using algebra and/or substitution.

$\lim_{x\rightarrow 7} 3.14x^2-5x+1$
$\lim_{x\rightarrow 50} 10$
$\lim_{x\rightarrow -4}\frac{x^2+8x+16}{(x+4)^2}$
$\lim_{x\rightarrow 2}\frac{x^2-4}{x-2}$

Previous Lesson

Back to Course

Next Lesson