PRAXIS: Derivatives Basics
Let \(f\) be given by the graph below, and let the \(y\)-values represent the value (in thousands) of a particular metal (like gold or silver) over \(x\)-months.
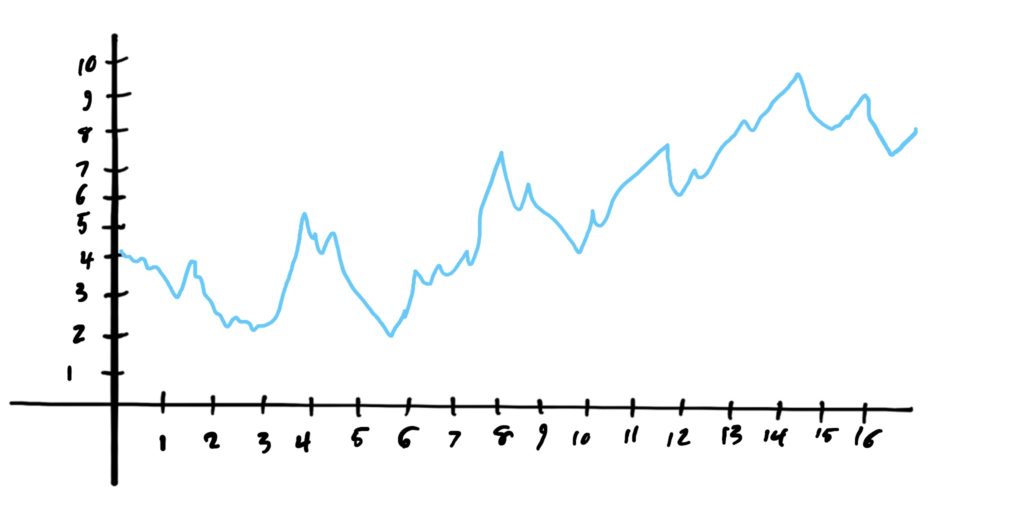
- Find the average rate of change of \(f\) between \(x=3\) and \(x=11\).
- Find the average rate of change of \(f\) between \(x=3\) and \(x=6\).
- Find the average rate of change of \(f\) between \(x=3\) and \(x=3.1\).
- Find the average rate of change of \(f\) between \(x=3\) and \(x=3.01\).
- Guess the rate of change at exactly \(x=3\) using your answers to the last four problems.
- What does your answer to the last question represent in terms of the context of the question?
Compute the following derivatives at the given \(x\)-value (use the \(h\)-form first, then plug in the \(x\)-value).
- \(f(x)=5x^2\) at \(x=1\)
- \(g(x)=2x^3\) at \(x=-2\)
- (Bonus +10) \(h(x)=\frac{1}{x}\) at \(x=1\)
Follow the instructions for each problem as given below.
- Find the instantaneous rate of change of \(f(x)=6x+1\) at \(x=0\)
- Find the line tangent to the graph of \(f(x)=x^2\) at \(x=2\)
- Find the line tangent to the graph of \(g(x)=3x+1\) at \(x=100\).
