Optimization Applications

What all this stuff on finding mins and maxes is for

You might have been wondering “why do we bother with finding mins and maxes of a function. The answer is simple: if we model different phenomena using functions and we want to find when the best and worst case occurs, we now have a way to do that.

Sometimes we are using functions to model more complicated phenomena, such as in profit and cost functions which trend with a certain data set… sort of like an average. Other times, we are using functions to directly model situations more directly. We will give several examples of both.

Note what follows are word problems that take time, thinking, and patience. Make sure you have all three available to you… especially patience. Don’t give up! Use the following steps for solving word problems whenever possible.

Example: Suppose you are given a sheet of cardboard that measures 12 inches wide and 8 inches tall that you want to turn into an open-top box by cutting out the corners of the sheet and folding up the flaps (depicted below). Note that the cutouts should be square. What should the width of the cutouts be if the box needs to have maximum volume? What is maximum volume of the box?

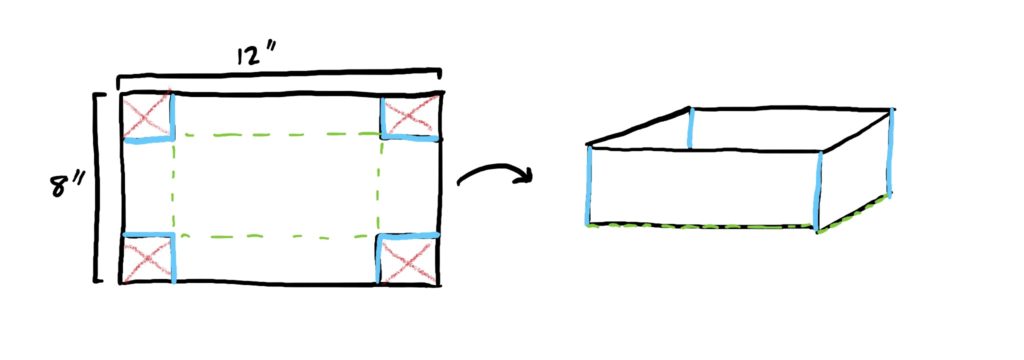
After reading the problem several times to wrap one’s head around what is being asked and what is being given (STEP 1), we will draw a picture and label all the quantities given to us. We want to optimize volume, so let’s call our volume \(V\). We have the sheet’s length and width, so we can simply label those as below. We also know that the corner cutouts have the same length and width, but we don’t know how big they are, so we will call the width/length \(x\). See diagram for all this good stuff properly labeled. (STEP 2).

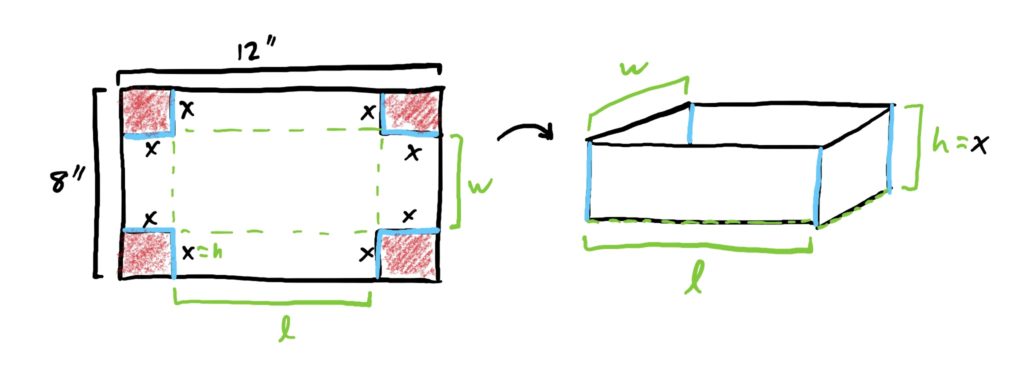
Now, for STEP 3, we want to write an equation (or two) relating all these different quantities. We want to find the size of the cutout that gives us the best possible volume, so let’s build a function relating \(V\) to all our other quantities.

We know that the volume of the box is given by \(V=l\cdot w\cdot h\), where \(l,w,h\) are the length, width, and height of your box, respectively. Since all three depend on the size of our cutout of width \(x\), we need to come up with an expression for each of \(l\), \(w\) and \(h\) that depends only on \(x\).

We know that \(h=x\); the size of the cutout, based on the diagram. The length and width can be similarly calculated as \(l=12-2x\) and \(w=8-2x\), respectively, because in order to get the length or width of the box after all the flaps have been folded up, we are removing two corners of size \(x\) from the length and width. This is depicted below.

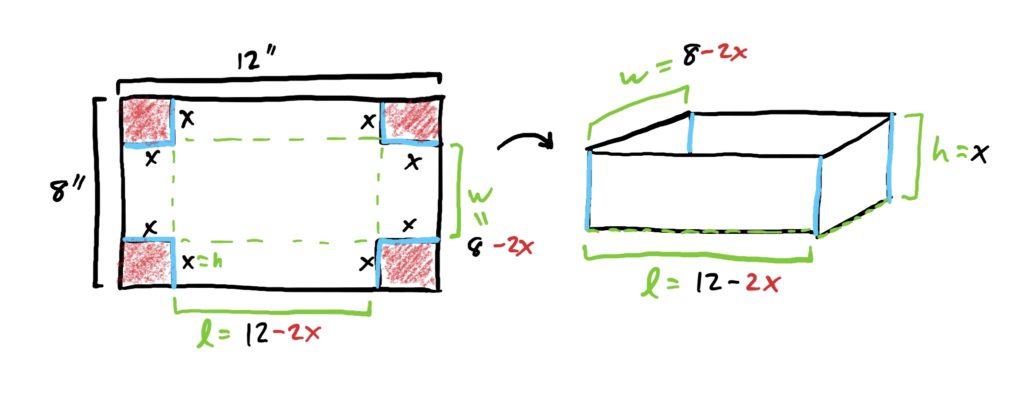
Substituting \(h=x\), \(l=12-2x\), and \(w=8-2x\) into the volume formula, we get \(V=(x)(12-2x)(8-2x)\). Thus, we have a single function in terms of one variable \(x\). This ends STEP 4.

Now we need to find the critical points and classify them. Since we are optimizing volume, we will derive the volume equation as given above, but we will first expand/distribute everything first (much easier to derive than using the product rule twice). This gives us

$$V(x)=4x^3-40x^2+96x$$

Now, we derive this thing, set it equal to zero, and solve for \(x\). The following work gives us the critical points \(x=1.5695\) and \(x=5.0972\).

Now, we need to classify these critical points. Let’s use the second derivative test. Note that \(V^{\prime\prime}(x)=24x-80\), and so \(V^{\prime\prime}(1.5695)=24(1.5695)-80=-42.332\) which is negative, indicating that \(x=1.5695\) is a local max. Similarly, \(V^{\prime\prime}(5.0972)=24(5.0972)-80=42.3328\) which is positive, giving us a local min. STEP 5

Therefore, Volume is maximized when the size of the cutouts is \(x=1.5695\) inches. We also want to know what that maximum volume is. So, just plug your \(x\) into the original volume formula: \(V(1.5695)=4(1.5695)^3-40(1.5695)^2+96(1.5695)=67.6036\) \(in.^3\). This wraps up the problem!

Optimal Finances

Perhaps one of the most useful things optimization can do for us in the financial world is help us determine pricing of goods to maximize profits or minimize losses. One can also use the techniques of calculus to find the best possible duration of a discount, or even how often to run a sale to maximize quantity sold. We look at applications such as these here and in the examples below.

Maximizing Revenue with Optimal Pricing

Suppose an internet store sells t-shirts. Over about one year’s time the business offers many different discounts on their t-shirts in order to gather data. They find that at the price of $30 per t-shirt, they can sell 500 t-shirts per day, and for every dollar they decrease the price, the number of sales increases by 20 t-shirts more per day. What should the price per t-shirt be if revenue is to be maximized? Also, what is the maximum revenue you can hope to generate from selling t-shirts (merely by changing pricing only)?

Here, if one follows the steps mentioned in the last section, we should certainly re-read the problem multiple times, completing step 1, but there really isn’t too much to sketch here for step 2, so we will skip that part of the step. However, we can start identifying all the different quantities given in the problem.

Our quantities are: number of sales \(s\) , price per shirt \(p\), amount of price decrease \(x\), and revenue \(r\). We want to maximize revenue, so we will need to build a function for revenue based on these other quantities, which in turn, will be based on the one thing we control: amount of price decrease.

We know in this situation that \(revenue = (price\ per\ shirt) \cdot (number\ of\ sales)\), or, using our symbols

$$r = p\cdot s$$

We want \(r\) to be a function only of \(x\) (i.e. a function in terms of what we control: how much we decrease the price). So we need to write \(p\) and \(s\) in terms of \(x\) to make this happen.

Note that we started our pricing at 30$ per shirt, and we are reducing our price by \(x\), so based on whatever \(x\) is, our price per shirt is given by

$$p(x)=30-x$$

We also know from the problem that for every dollar \(x\) we drop the price, the number of sales per day increases by 20, starting at 500 if we don’t decrease the price at all. Thus, our expression for \(s\) in terms of \(x\) is given by:

$$s(x)=500+20x$$

This completes step 3. To handle step 4, simple take your \(p(x)\) and \(s(x)\) and plug it into your revenue function. You will get:

$$\begin{align}r(x)=(30-x)(500+20x)\\&=-20x^2+100x+15000\end{align}$$

This completes step 4. For step 5, we find the critical points of \(r\) and find us the value for \(x\) where revenue is maximized (i.e. find a local max). The work for finding the critical points and classifying them is shown below in case you want to see it all worked out.

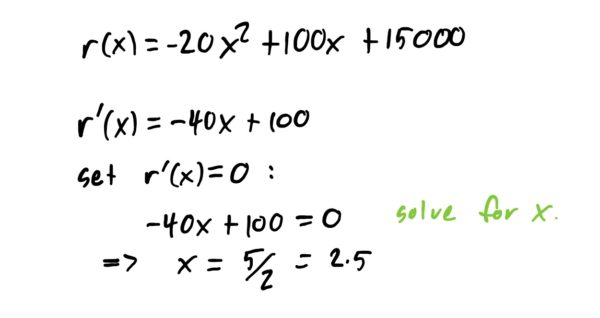
By the above work, we found that the only critical point is at \(x=2.5\) (end of step 5). This indicates that we need to reduce the price to $27.50 (i.e. a $2.50 reduction) to maximize revenue. If we DID price our shirts at $27.50, our maximum possible revenue per day would be

$$r(2.5)=-20(2.5)^2+100(2.5)+15000=15,125$$

(End of step 6)

If you’re curious, you can compare that to what the business was bringing in at its original pricing:

$$r(0)=-20(0)^2+100(0)+15000 = 15000$$

It’s a small difference, but a few minutes of calculation just earned your business an extra 125$ per day.