Multiplying Polynomials (aka “Distribution” or “FOILing”)
Single-Term Distribution
In a previous lesson, we discussed how, when combining multiples of two quantities, such as in a problem like \(4(3x^2+5x)+3(x^2-2x)\), one could distribute the \(4\) to each term in \(( 3x^2+5x)\) and distribute the \(3\) to each term in \((x^2-2x)\), so that
$$\begin{align} 4(3x^2+5x)+3(x^2-2x) &=(12x^2+20x)+(3x^2-6x).\end{align}$$
The same idea holds when, instead of having a number out in front of a quantity, you have a variable (or an expression with variables in it). For instance, note that the \(x^2\) can be distributed as if it were a number in the product \(x^2\cdot(5x^3-2x^2+7)\) as follows:
$$\begin{align}x^2\cdot(5x^3-2x^2+7)&=x^2\cdot 5x^3-x^2\cdot 2x^2+x^2\cdot 7\\&=5x^5-2x^4+7x^2\end{align}$$
where we added the exponents to get the final answer (by the product rule for exponential expressions).
The reason this works the same way as distributing a number is because variables represent unknown numbers, and because of this, expressions like \(x^2\) also represent unknown numbers (if we knew what \(x\) is, then we would be able to compute \(x^2\)).
Expand the following product \(x^3\cdot (2x^2-7x+1)\) by distributing the \(x^3\) through the second quantity.
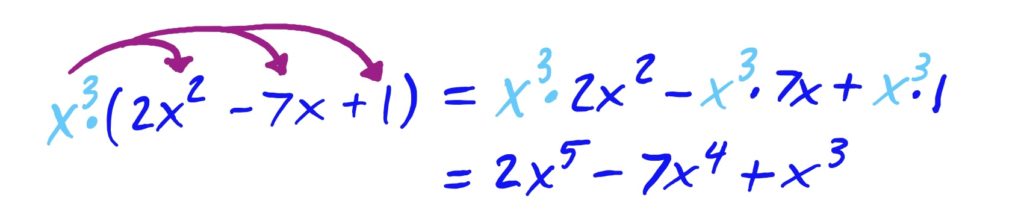
The same idea applies when dealing with distribution of several-term quantities; it just gets complicated/messy.
FOILing and Distribution of Several Terms
The process of distribution is often called expansion or expanding. The result of distributing out a product of two quantities is (similarly) called the expansion of the product.
The idea is to distribute both the \(x^2\) and the \(3\) to every term in \((5x^2-2)\), and then add together the results. This is depicted below.
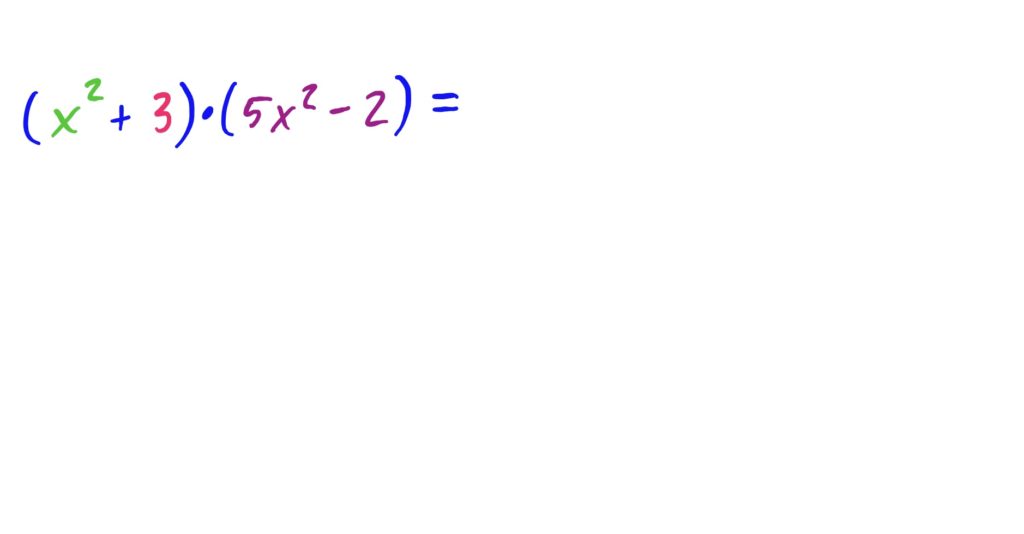
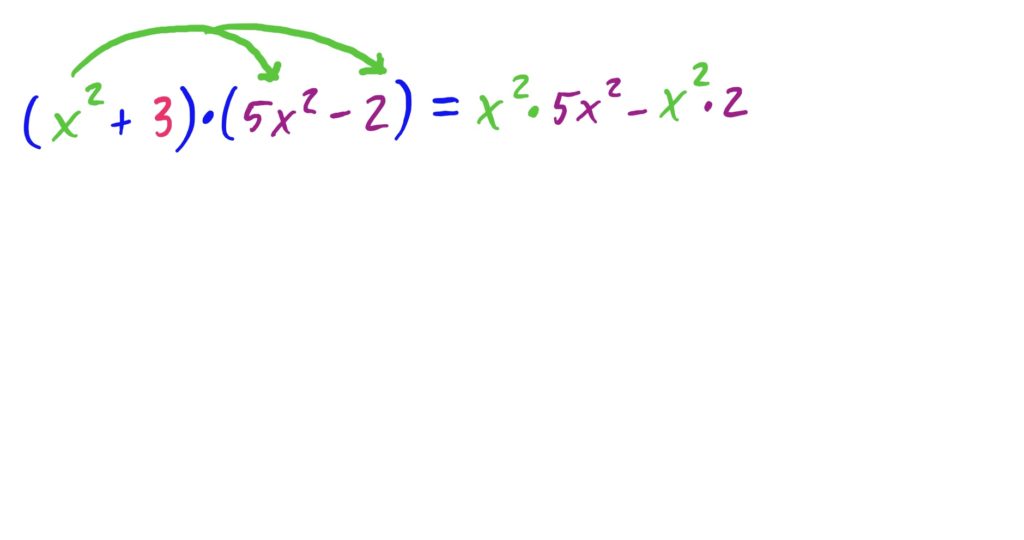
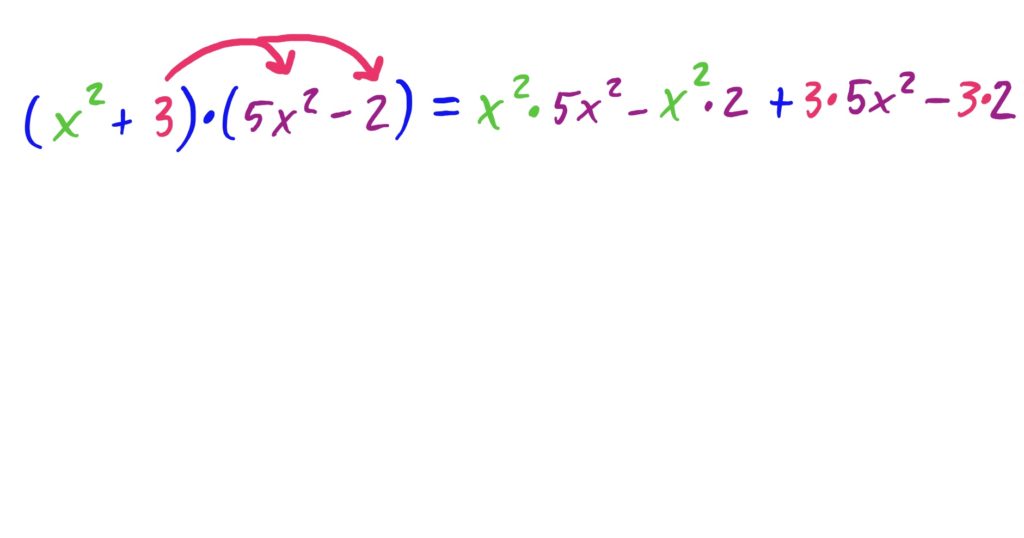
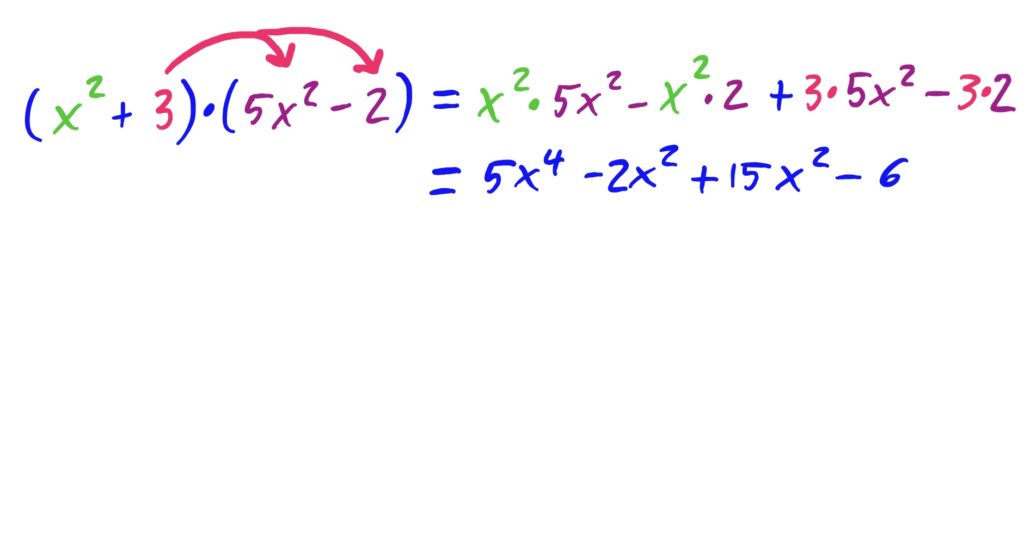
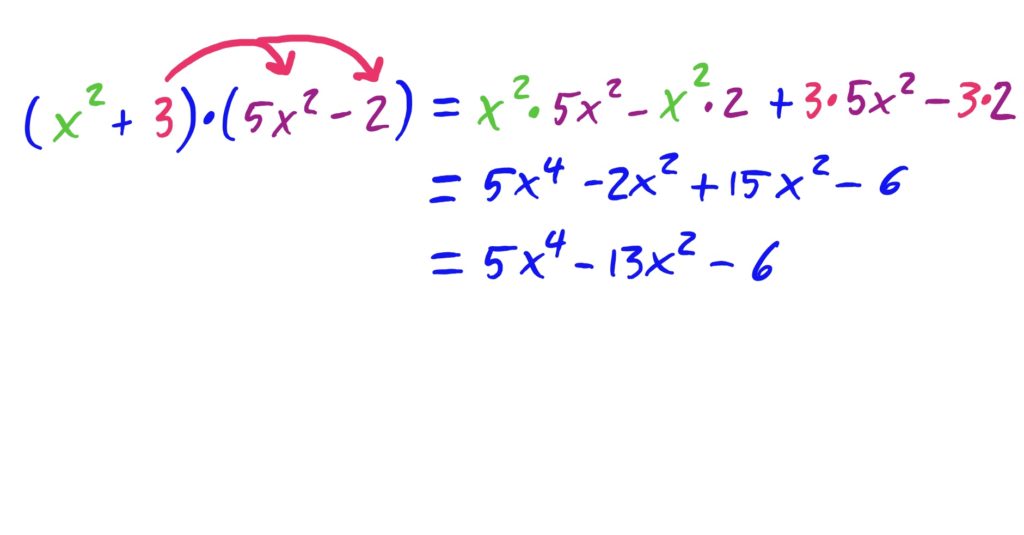
The idea is to distribute both the \(x^2\) and the \(-2\) to every term in \((x^2+2x+1)\), and then add together the results. This is depicted below.
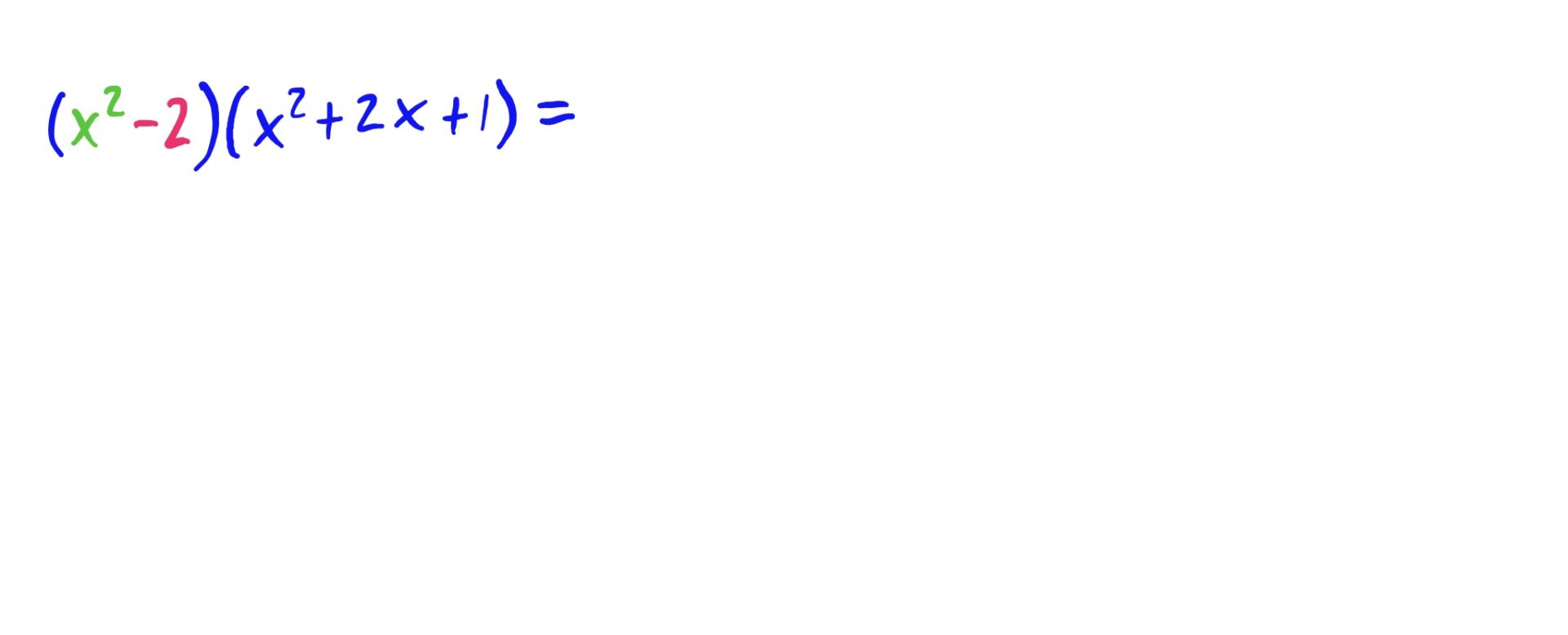
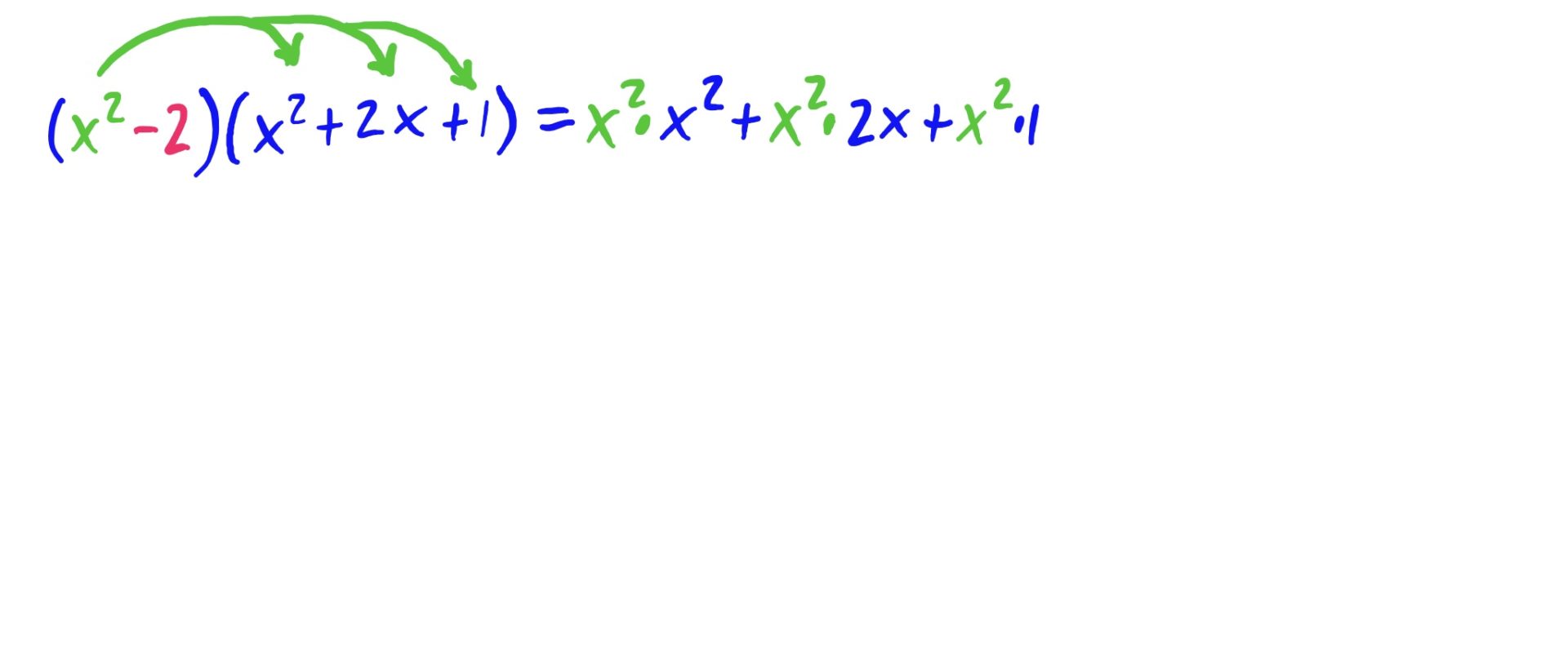
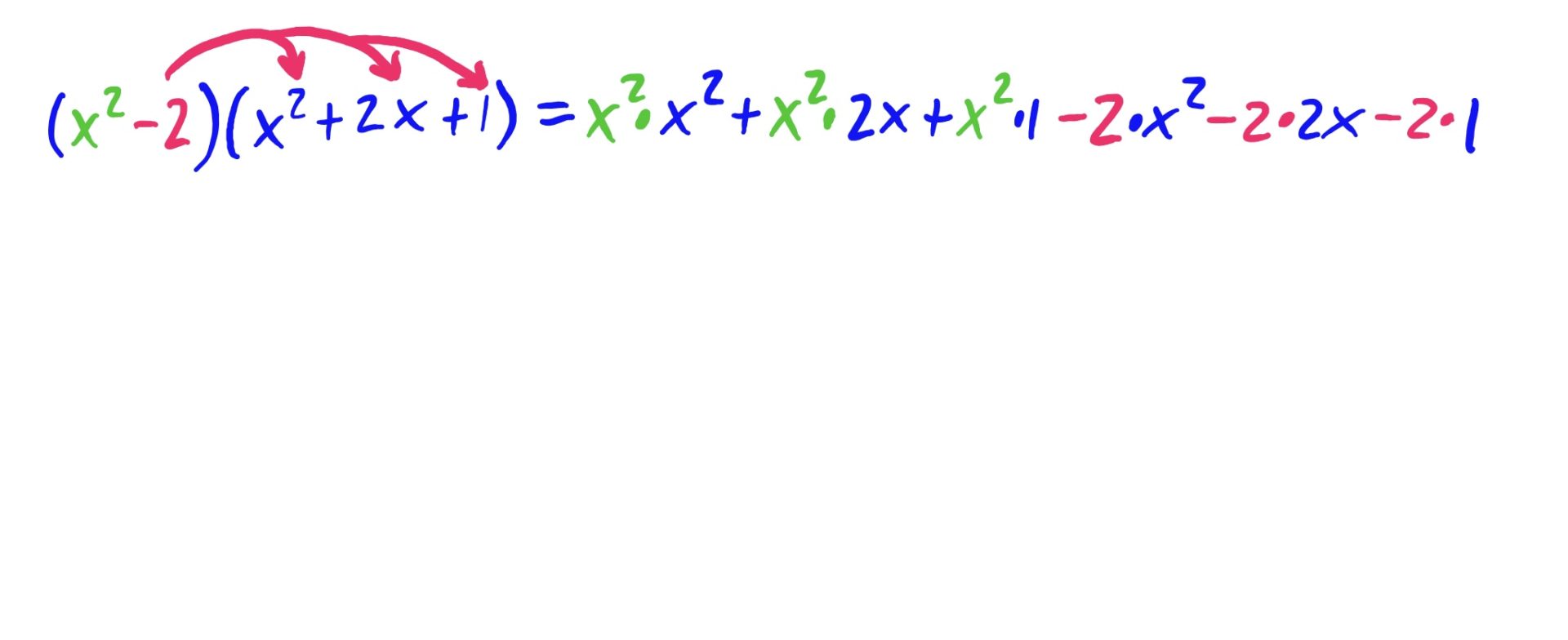
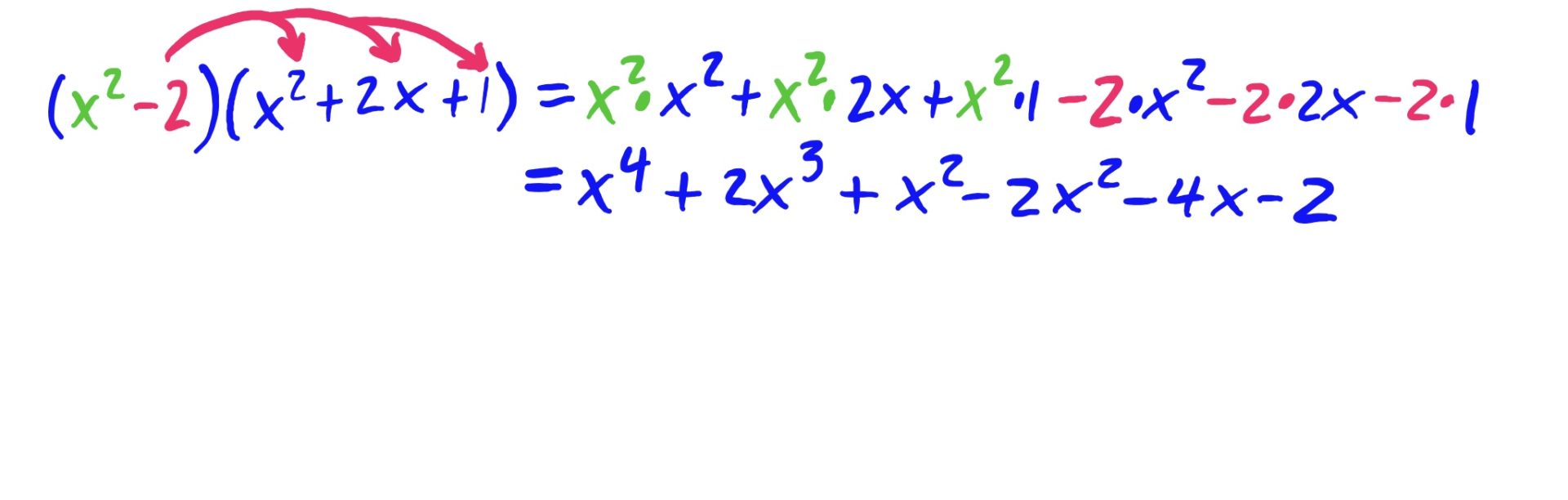
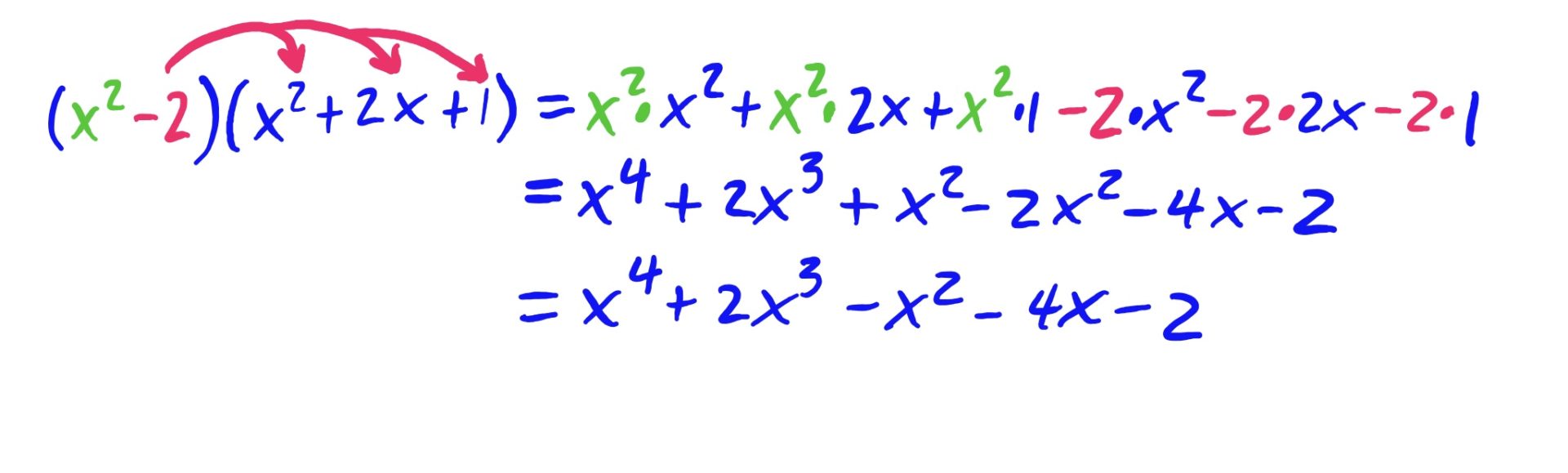
\(x^2+x\)
Multiply each term inside the parentheses by the \(x\) on the outside of the parentheses, and add the results together. There are no like-terms that can be combined, so there is nothing more to do beyond this point.
\(3x^4+2x^3-4x^2\)
Similar to the first example, distribute/multiply the \(x^2\) with each term inside the parentheses, then add the results, combining like-terms (there are none in this case).
\(-x^3-11x^2+2x\)
\(-3x^3-8x^2-5x\)
This is a factorization of a difference of squares. More on that later.
\(x^2-1\)
\(x^3+6x^2+6x+5\)
\(x^4+4x^3+4x^2\)
\(3x^3+2x^2-3x-2\)
\(8x^3+12x^2+6x+1\)
\(-3x^4+7x^3+8x^2+5x+1\)
\(4x^6-16x^5+16x^4+4x^3-8x^2+1\)
\(x^4-2x^2-4x\)
