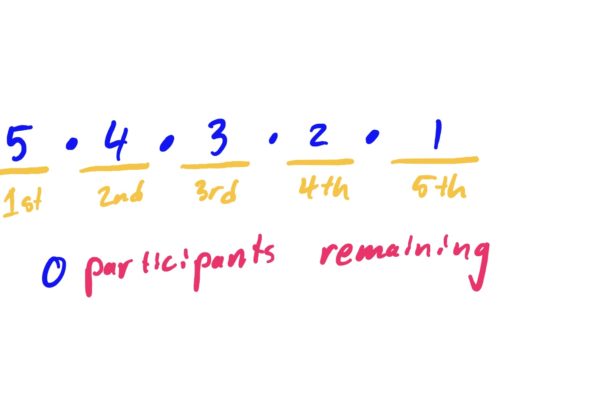Multiplication Principle and Permutations
The Multiplication Principle for Counting
Let’s start with a simple problem.
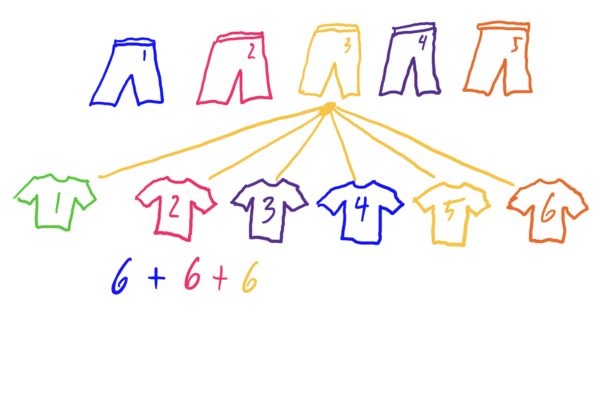
Suppose you are quarantining during a pandemic and these days you are only wearing sweatpants and tee shirts. You have five different pairs of sweatpants and six different tee shirts. Since you are bored and have nothing better to do, determine how many outfits you could wear.
Solution? 30 outfits.
To see how this works, notice that for each pair of sweatpants, you can wear \(6\) different tee shirts. Since this is the case for each of your \(5\) pairs of sweatpants, you have \(30\) combinations/outfits. This idea is illustrated in the sequence below.
Lets look at a similar problem.
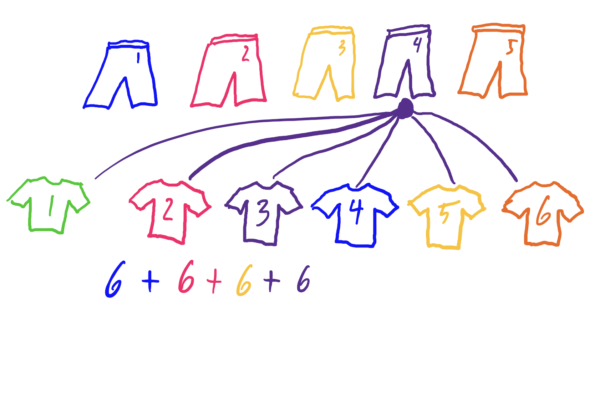
Suppose you not only have sweatpants and tee shirts, but you also think it’s probably wise to put some underwear on as well. So, in total, you have five pairs of sweatpants, six tee shirts, and seven pairs of underwear. How many outfits can you make with these clothing articles?
Solution: 210 outfits!
To see this, if we represent our sweatpants with five green dots, tee shirts with \(6\) red dots, and underwear with \(7\) blue dots, notice that for each pair of sweatpants, there are six choices for tee shirts, and for each of those tee shirt choices you have seven choices for underwear. See the following diagram.
So, it follows that you have \(5\cdot 6\cdot 7\) outfits total! This illustrates the following principal.
Put another way, in more set theoretic terms, in \(A_1, A_2, A_3, …, A_n\) are sets with orders \(a_1, a_2, a_3, …, a_n\), then the order of \(A_1\oplus A_2 \oplus A_3 \oplus … \oplus A_n\) is \(a_1\cdot a_2 \cdot a_3\cdot …. \cdot a_n\).
There are natural examples for where the multiplication principle cannot be applied, where the choice of one object interferes with teh choice of another. This is especially the case when you are choosing different objects from the SAME set. For these sorts of situations, we need permutation and combination techniques.
Permutations
Question: Suppose a science competition is judging five undergraduate science research projects, and the judge’s panel needs to choose contestants for a first, second, third, fourth, and fifth place. How many ways can the judge’s panel do this? That is, how many ways can the judges arrange the contestants so they are placed in first through 5th place?
One of the best ways we can solve problems like this is by “filling slots.” In our case, we can draw five slots, each representing the five possible positions that the contestants can be placed in. Then, for each slot, determine how many ways that slot can be filled with the number of contestants remaining.
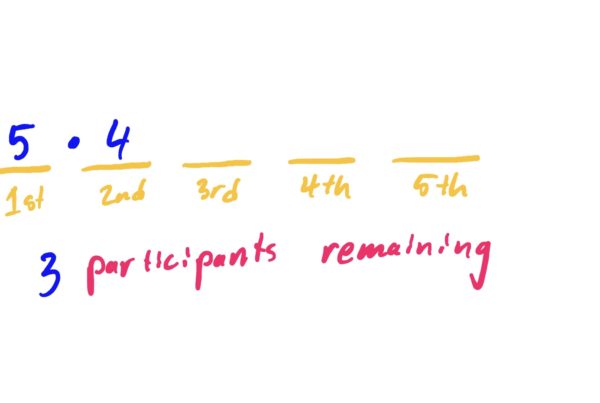
There are five ways to fill first place, leaving four contestants remaining. So, for each of the contestants that could be in first place there are four possibilities for second place, so we multiply the five possibilities for first by the four possibilities for second.
Once a second place candidate has been chosen, there are three candidates remaining for third place. So, for each choice of first and second place, we have three choices for third place, and so we multiply the five possibilities for first, the four possibilities for second, and the three possibilities for third.
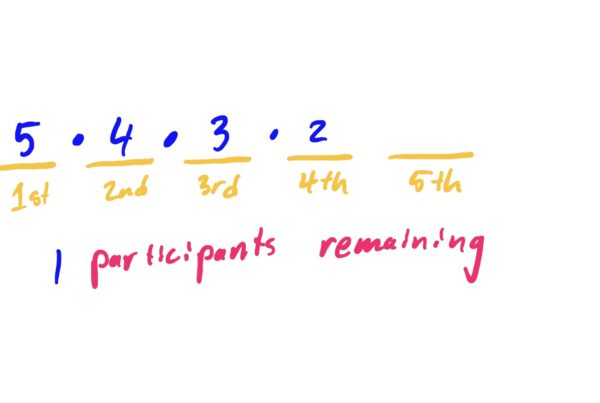
Similar reasoning allows us to determine the number of possibilities for fourth and fifth place, giving us a total of \(5!\) ways we can choose first place through fifth place.
What if instead of needing to choose a placing for all five contestants, we only wanted to choose a first, second, and third place?
Question: How many different ways can we choose a first, second, and third place out of five candidates?
We can use the same method of slot-filling as we did before, but instead of working all the way down to fifth place, we only work down to third.
Note that there are five ways we can choose a first place, four ways we can choose a second place (once a first place is chosen), and three ways we can choose a third place (once first and second place is chosen), because as we fill each slot, we reduce the number of candidates that we have to choose from. We then multiply the number of possibilities for each slot to get the final result. This is illustrated below.
Note that in either of the two examples above, we were arranging objects in a specific order; it mattered who came in first, second. and third place. So, when we are concerned with the arrangement of a certain number of objects out of a larger collection, we can use the following formula.
A specific arrangement of \(m\) objects out of a larger collection of \(n\) objects is often referred to as a permutation of \(m\) objects out of \(n\). So, the formula above gives us the total number of permutations of \(m\) objects out of \(n\).
Suppose we are trying to arrange \(m\) objects out of a larger total of \(n\) objects. That means that we have to fill a total of \(m\) slots using these \(n\) total objects.
The number of ways of filling the first slot is \(n\). the number of ways of filling the second slot is \((n-1)\) (i.e. one fewer than we started with, since we already placed one of the \(n\) objects in the first slot). The number of ways of filling the third slot is \((n-2)\) for similar reasons (we already filled the first two, reducing the number objects to choose from for the third slot by 2).
Continuing the process all the way down until we fill the \(m\)th slot, we compute the total number of ways we can arrange \(m\) objects out of \(n\) by multiplying the total number of ways we can fill each.
If we wanted to arrange all \(n\) of these objects, we would need to fill \(n\) slots, and so would end up multiplying \(n\cdot (n-1)\cdot (n-2)\cdot … 3\cdot 2\cdot 1\).
But since we are stopping after filling the first \(m\) slots, we need to “get rid of” all of the extra multiplication for the slots we don’t need to fill. To do that, we divide away the extra arrangements on the remaining \((n-m)\) elements (had we arranged all \(n\) of them).
