Module 3 Homework Problems
Complete the Following Problems
For each of the following problems 1-9, let \(A=\{1,2,…,8,9,10\}\) and \(B=\{3,4,5,…,10,11,12,13\}\), and let \(R\) be the relation defined as \(R=\{(a,b)\vert a\in A, b\in B,\ \text{and}\ a\leq b\}\).
- True or False: \(2R10\); explain
- True or False: \(10R3\); explain
- True or False: \(4R4\); explain
- True or False: \((11,4)\in R\); explain
- True or False: \((8,11)\in R\); explain
- True or False; \((5,14)\in R\); explain
- Find the set of all \(b\in B\) such that \(9Rb\)
- Find the set of all \(a\in A\) such that \(aR3\)
- Is \(R\) homogeneous or heterogeneous? Why?
- Give an example of a homogeneous relation on a set that you define. Aim for coming up with something that is different from any example covered on this site.
- Build a relation from a set of ordered pairs that is NOT reflexive (i.e. come up with an example relation of your own that is not reflexive).
- Build a relation from a set of ordered pairs that is reflexive, but NOT symmetric
- (Bonus +10) Build a relation from a set of ordered pairs that is reflexive, symmetric, but NOT transitive.
- Is the relation \(“\geq”\) on the set of real numbers an equivalence relation? Why or why not?
- Let \(S\) be the equivalence relation defined on \(S=\{2,3,4,5\}\) such that \(S=\{(2,2),(2,3),(3,2),(3,3),(4,5),(4,4),(5,4),(5,5)\}\). Find the equivalence classes \([2]\) and \([3]\). Are there any other equivalence classes of \(S\) different from \([2]\) and \([3]\)?
Let \(f\) be defined by the potato diagram below, for questions (16-22)
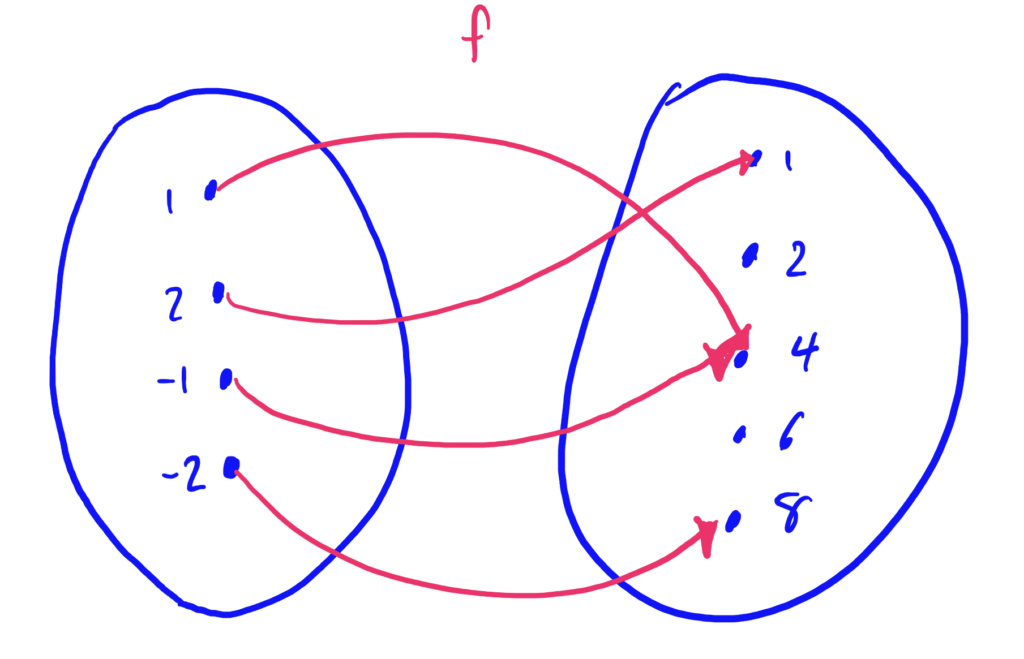
- Find the image of \(-1\) and \(-2\)
- Find the image of \(S=\{1,2,-2\}\)
- Find the preimage of \(4\)
- Find the preimage of \(M=\{1,8\}\)
- Find the domain of \(f\)
- Find the range of \(f\)
- Find the codomain of \(f\).
- Give an example of a function that is injective but NOT surjective
- Give an example of a function that is surjective but NOT injective
- Give an example of a function that is neither injective nor surjective
- (Bonus +10) Let \(f:A\rightarrow B\) be a function, where \(A\) is the domain and \(B\) is the codomain of \(f\). Suppose \(|A|=|B|\). Is it possible for \(f\) to be surjective but not injective? How about injective, but not surjective?
Let \(f\) be the function defined by the graph below, where the tick marks on the \(x\) or \(y\)-axis represent whole numbers.

- Is \(f\) onto? Explain.
- Is \(f\) one-to-one? Explain
- What is the image of \(x=2\)?
- What is the image of \(\{1.5,-1.5\}\)? (Estimates are okay here)
- What is the preimage of \(\{2\}\)?
- What is the domain of \(f\)? What is the range?
