Function Composition: Plugging One Function Into Another

Function Composition as a Concept

Function composition is literally nothing more than chaining together functions, taking the output of one function and feeding it into another function as input. Think of function composition as “daisy-chaining” two or more machines together, or forming an assembly line. See below.

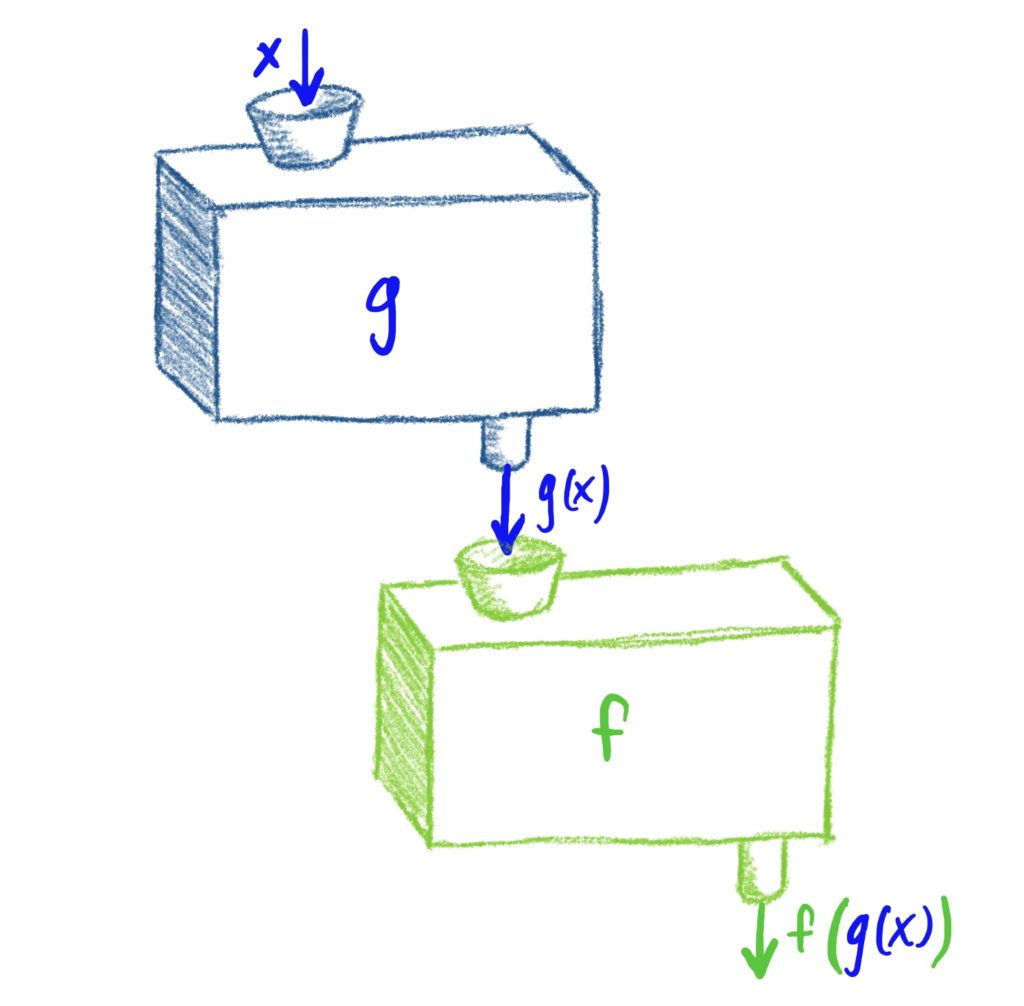
In the above, we are first feeding some input \(x\) into the machine/function \(g\) and then taking the output of that function, namely \(g(x)\), and then feeding that as input into \(f\), which then produces the final output \(f(g(x))\).

In what follows, we will be demonstrating how this “chaining together” of functions works in terms of the several different ways we represent functions.