PRAXIS: Optimization Applications
- Refer to the cardboard box cutout diagram as shown in the key takeaways of the “Optimization Applications” lesson. Suppose instead that our initial sheet of cardboard was 30 inches long and 20 inches wide. How large would the corner cutouts need to be in order to maximize volume?
- Suppose you are tasked with designing a cylindrical drinking cup out of plastic (i.e. a cylinder with an open top). If your surface area is restricted to 75\(cm^2\), what should the height and radius of the cup be to maximize volume?
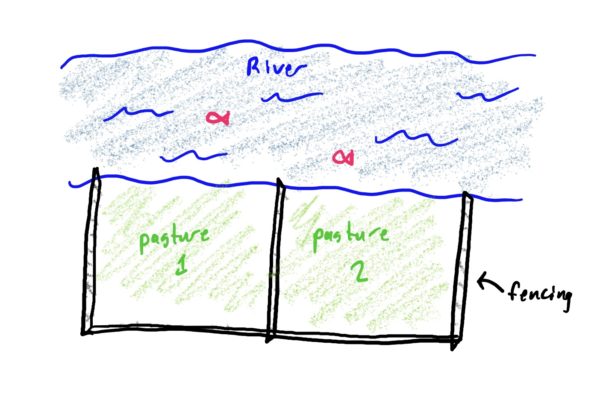
- Suppose we want to create two side-by-side feeding pastures along a riverbank, both of which are enclosed by fence. Given that we only have 1000 yards of fencing to use, what should the dimensions (length and width) of each pasture be so that the area of each is maximized? See image below.
- Suppose you’re running a company that sells toasters and that your pricing per toaster is determined by the function \(p(x)=40-0.25x\) where \(x\) is the number of toasters sold. Cost of manufacturing each toaster is $\(10\). How many toasters need to be sold to maximize profit?
- A hotel chain is able to sell out all of their 200 rooms if they charge $145 per night. For every $15 they increase the price, the number of rooms occupied drops by 5. Furthermore, on average, each occupied room spends $10 per night on room service. The housecleaning service that the hotel employs charges a base fee of $500 per night plus an additional $20 per room per night. What should the hotel charge per night to maximize profit? What is the maximum profit that the hotel can expect?
