PRAXIS: Concavity, Inflection Points, and Second Derivative Test

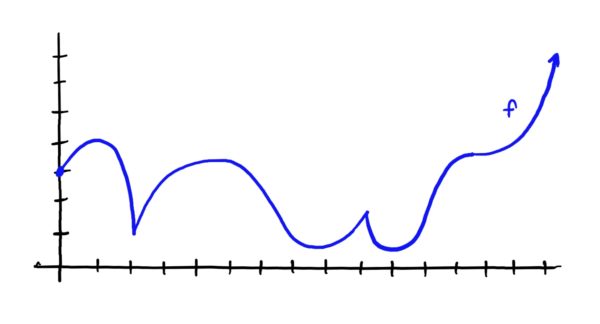
1. Let \(f\) be the function defined by the graph below. Determine the intervals where the graph of \(f\) is concave up and concave down. Also, identify all inflection points.

For each of the following functions, determine all intervals where the function’s graph is concave up and concave down. Identify all inflection points. If an interval is provided, only do what the last sentence asked on that interval and ignore what happens outside of the given interval.

2. \(f(x)=x^3+5x^2-2x+1\)
3. \(f(x)=x^4-4x^2+3\) on the interval \([-1,5]\)
4. \(g(x)=7x^3-2x+5\)
5. \(h(x)=(x-4)^4\)
6. \(J(x)=(x+2)^3\) on the interval \([-1,3]\)

For each of the following functions find all critical points (if there are any) and identify them as local mins or maxes using the second derivative test. If the second derivative test is inconclusive, use the first derivative test to classify the critical point.

7. \(f(x)=x^3-x+5\)
8. \(g(x)=5x^2+2x+1\)
9. \(J(x)=\frac{x^3}{3}-x^2+2x+1\)
10. \(h(x)=(x-1)^4\)