PRAXIS: Extrema
Let \(f\) be the function defined by the graph below.
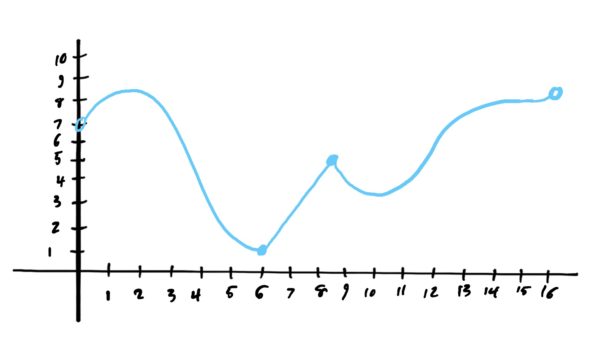
- Find all local mins and maxes of \(f\).
- What values does \(f\) attain at each of these local extrema?
- What are the global maxes (if any)? What are the global mins (if any)?
Let \(g\) be defined by the graph below.
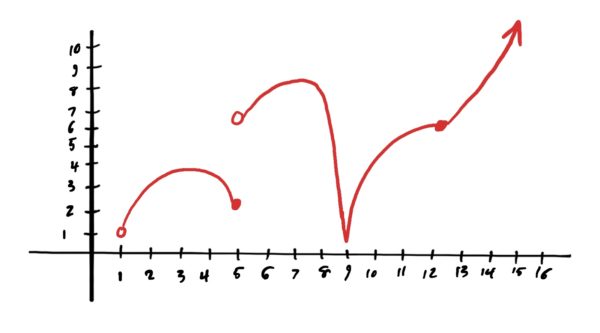
- Find all local mins and maxes of \(f\).
- What values does \(f\) attain at each of these local extrema?
- What are the global maxes (if any)? What are the global mins (if any)?
Let \(h\) be defined by the graph below.
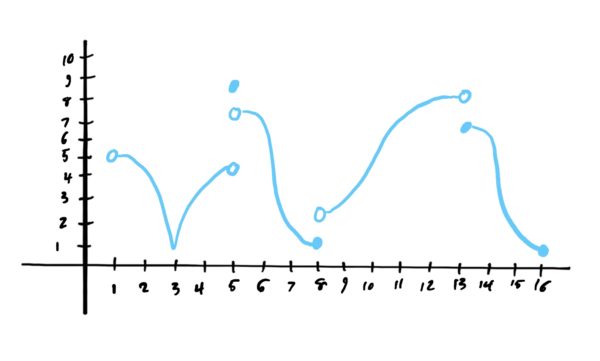
- (Bonus +5) Find all local mins and maxes of \(h\).
- (Bonus +5) What values does \(h\) attain at each of these local extrema?
- (Bonus +5) What are the global maxes (if any)? What are the global mins (if any)?
Find all critical points for the following functions, and classify each critical point as a local min, max, or neither.
- \(f(x)=x^3-6x^2+5x-2\)
- \(g(x)=-2.1x^3-8.52x^2+5.4x\)
- \(h(x)=x^5-2\)
Find the global min and max for the following functions on the given interval.
- \(g(x)=x^2+2x+4\) on the interval \([-3,1]\)
- \(f(x)=x^3-6x^2+5x-2\) on the interval \([-1,4.5]\)
- (Bonus +10) Find a function whose \(y\)-value at its global max(es) is the same as the \(y\)-value at its global min(s).
