PRAXIS: Derivatives Basics

Let \(f\) be given by the graph below, and let the \(y\)-values represent the value (in thousands) of a particular metal (like gold or silver) over \(x\)-months.

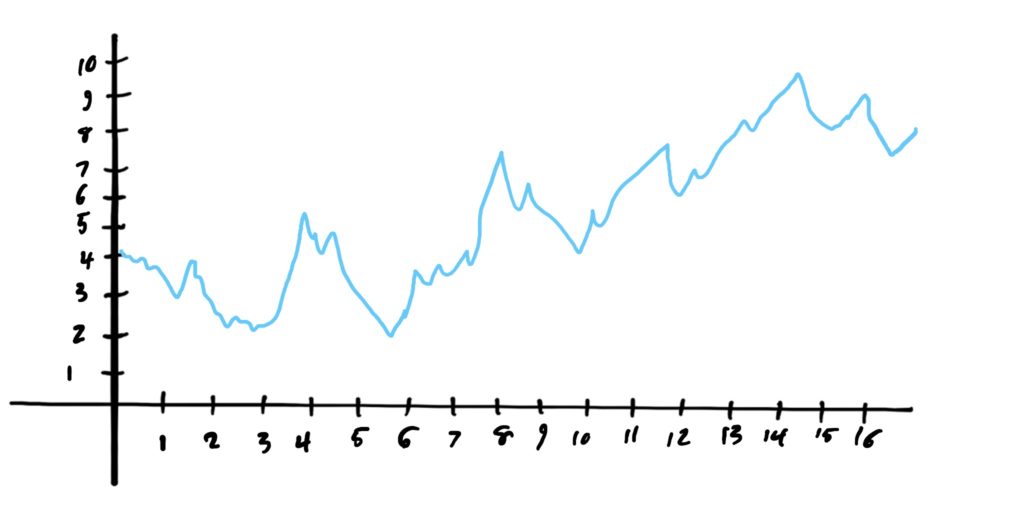
1. Find the average rate of change of \(f\) between \(x=3\) and \(x=11\).
2. Find the average rate of change of \(f\) between \(x=3\) and \(x=6\).
3. Find the average rate of change of \(f\) between \(x=3\) and \(x=3.1\).
4. Find the average rate of change of \(f\) between \(x=3\) and \(x=3.01\).
5. Guess the rate of change at exactly \(x=3\) using your answers to the last four problems.
6. What does your answer to the last question represent in terms of the context of the question?

Compute the following derivatives at the given \(x\)-value (use the \(h\)-form first, then plug in the \(x\)-value).

7. \(f(x)=5x^2\) at \(x=1\)
8. \(g(x)=2x^3\) at \(x=-2\)
9. (Bonus +10) \(h(x)=\frac{1}{x}\) at \(x=1\)

Follow the instructions for each problem as given below.

10. Find the instantaneous rate of change of \(f(x)=6x+1\) at \(x=0\)
11. Find the line tangent to the graph of \(f(x)=x^2\) at \(x=2\)
12. Find the line tangent to the graph of \(g(x)=3x+1\) at \(x=100\).