PRAXIS: Limits
- Use a table to guess the limit
$$\lim_{x\rightarrow 2} \sqrt{x^2+1}$$
Your table must have at least 10 rows: 5 values less than \(2\), and 5 values greater than \(2\). The \(x\)-values must also approach \(x=2\) as demonstrated in examples in the lesson(s).
- Use a table to guess the limit
$$\lim_{x\rightarrow -1} \frac{x^2+2x+1}{x+1}$$
Your table must have at least 10 rows: 5 values less than \(-1\) and 5 greater than \(-1\), similar to what you did above.
Let \(f\) be the function defined by the graph below
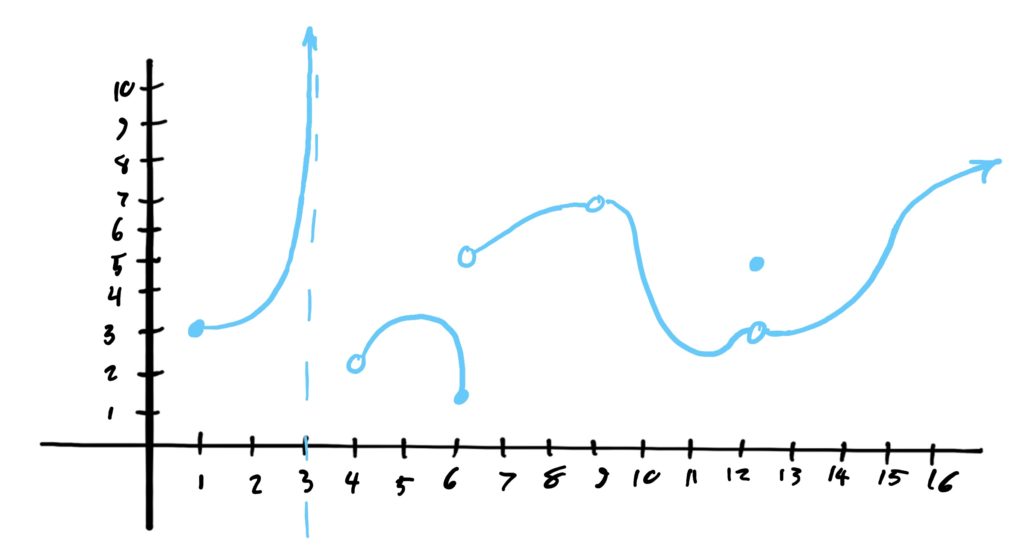
Find the following limits if they exist.
- \(\lim_{x\rightarrow 1^+} f(x)\)
- \(\lim_{x\rightarrow 4^+} f(x)\)
- \(\lim_{x\rightarrow 6} f(x)\)
- \(\lim_{x\rightarrow 9} f(x)\)
- \(\lim_{x\rightarrow 12} f(x)\)
- \(\lim_{x\rightarrow 15} f(x)\)
Find the following limits using algebra and/or substitution.
- \(\lim_{x\rightarrow 7} 3.14x^2-5x+1\)
- \(\lim_{x\rightarrow 50} 10\)
- \(\lim_{x\rightarrow -4}\frac{x^2+8x+16}{(x+4)^2}\)
- \(\lim_{x\rightarrow 2}\frac{x^2-4}{x-2}\)
