PRAXIS: Functions Fundamentals

For problems 1-5 refer to the following diagram describing the function \(f\).

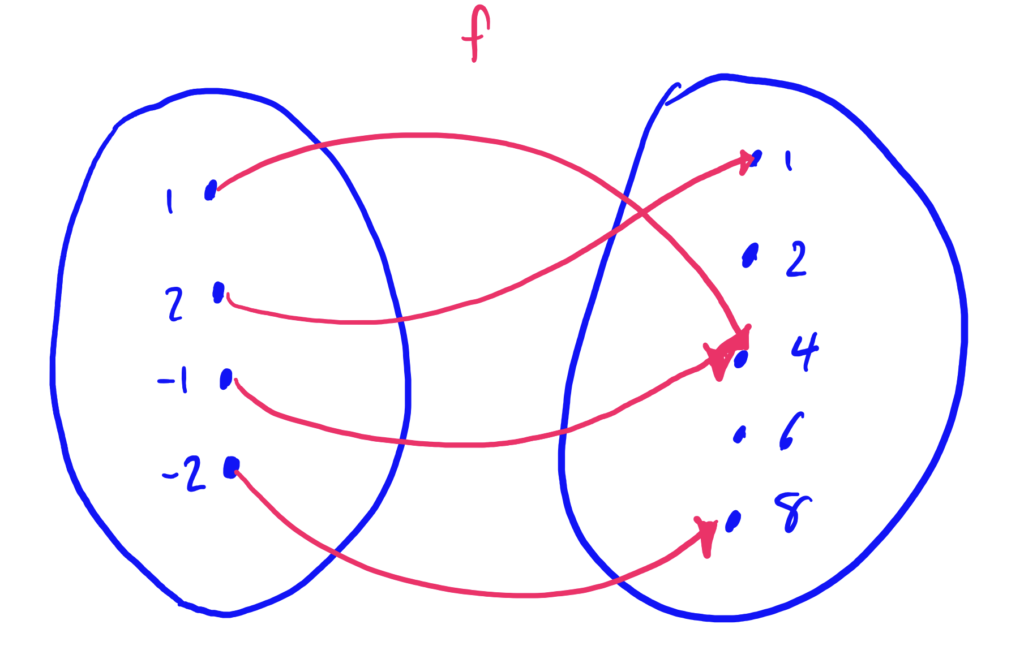
1. Is \(f\) a function? Why or why not?
2. Find \(f(-1)\) and \(f(-2)\)
3. Find the set of all inputs \(x\) such that \(f(x)=4\). (This is called the “pre-image” of \(4\))
4. Find the domain of \(f\).
5. Find the range of \(f\).

6. Let \(g(x)=x^2+5x-2\). Construct a table of \(x\) and \(y\)-values by choosing \(5\) \(x\)-values for your first column and plug these into \(g\) to get the corresponding \(y\)-values.
7. Graph the function \(g\) by using the points in the table you generated above.
8. Let \(h(x)=\frac{1}{x-3}\). Generate a table of \(x\) and \(y\)-values just like in number 6 above but with 10 \(x\)-values instead of 5. Do NOT use whole numbers for any of your \(x\) values.
9. Graph \(h\) using the table you generated above, plotting points.
10. Using a graphing calculator, draw the “actual graph” of \(h\) next to the one you drew in #\(9\). What are the differences? Why did your graph differ from the “actual graph?”