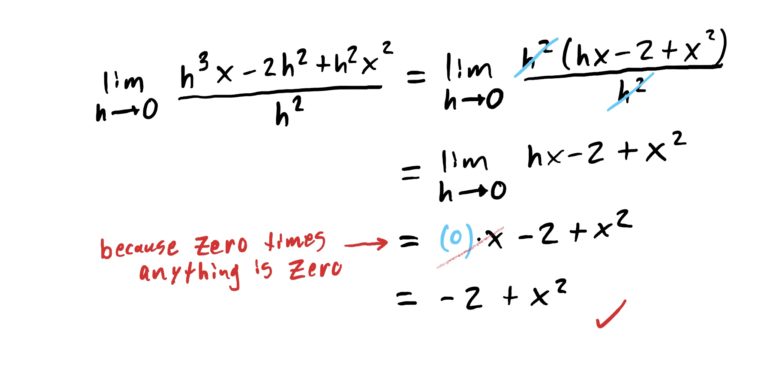Finding Limits Of Polynomials
Polynomials and Smooth Functions
Polynomials are perhaps the “nicest” class of functions we have to work with when it comes to Calculus. Recall that polynomials are sums or differences of monomials, and monomials are functions of the form:
$$c\cdot x^n$$
where \(c\in \mathbb{R}\) and \(n\in \mathbb{N}\). A few examples of polynomials:
$$x^2+5x+12\ \ \ \ \ \ \ 12.52x^5-3x^3-78x+1\ \ \ \ \ \ \ \frac{3}{4}x^{10}-x^7+\frac{15}{4}x+8$$. The stuff out in front of your powers’ of \(x\) can be any real number – decimals and fractions included. Powers can only be positive whole numbers.
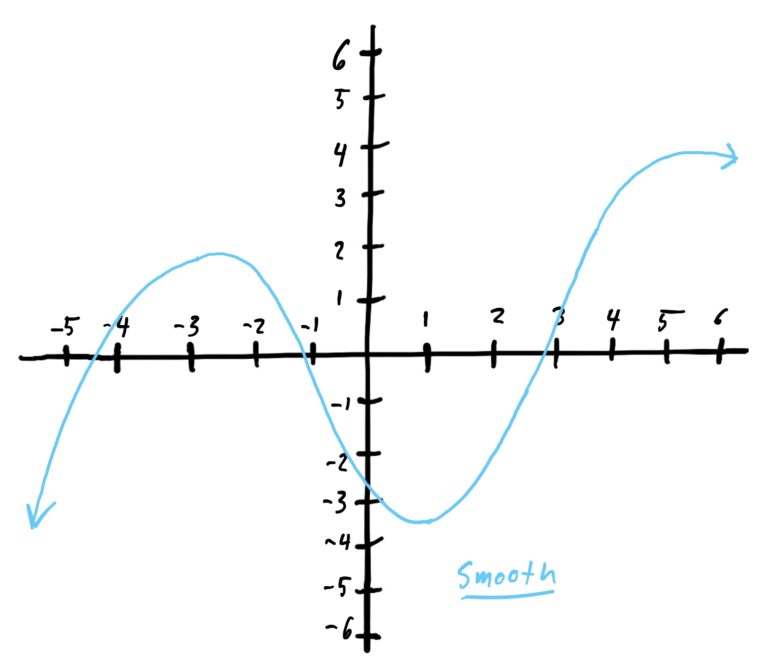
Polynomials have a medley of useful features. One of the most important is that of “smoothness” (yes, that is the mathematical term for it).
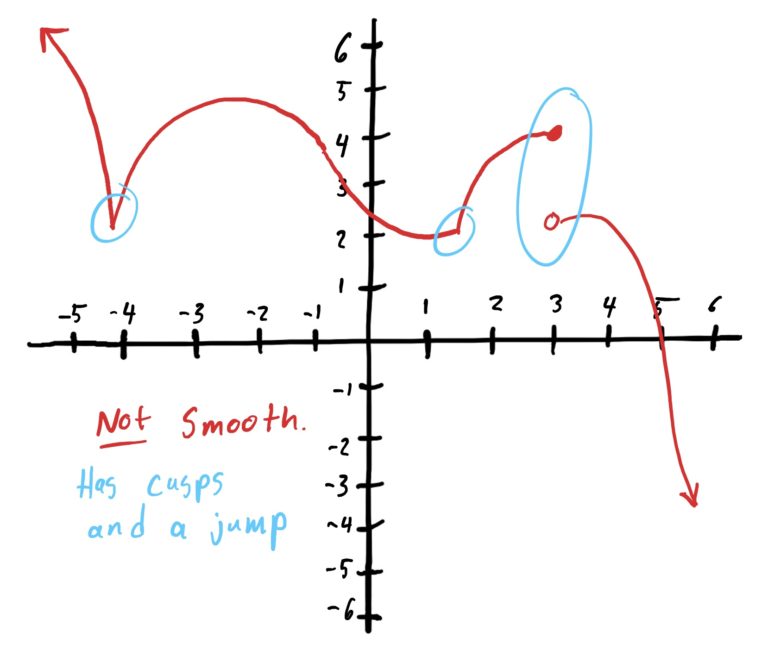
There is a mathematically precise definition of “smoothness,” but perhaps we will save it for another time. Below is an example of a smooth versus non-smooth function.
Limits of Polynomials
If given the rule for a polynomial, finding the limit of it at any \(x\)-value is simple.
The reason this works
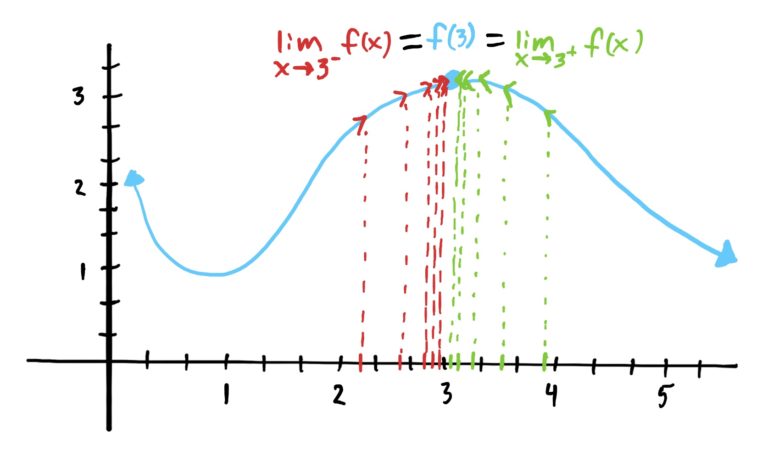
If a function is smooth on some interval, it implies that the function is defined at every \(x\)-value, and also that the left and right-hand limit of \(f\) at every \(x\)-value is the same AND equal to the function’s \(y\)-value at that point. This is illustrated in the graph below
Since \(f\) is a polynomial, we can compute the limit simply by plugging in \(x=2\)!
$$\begin{align}\lim_{x\rightarrow 2} x^3-2x^2+x-1 &= f(2)\\ &=(2)^3-2\cdot(2)^2+(2)-1\\ &=8-8+2-1\\&=1\end{align}$$
Incognito Polynomials
Sometimes we are given functions that look complicated, but in fact after a bit of simplification, turn out to be simple functions that are easy to work with and find limits of. For example, suppose we are given the function
$$f(x)=\frac{x^2+2x+1}{x+1}$$
Note that \(f\) is not defined at \(x=-1\) because it would make the denominator zero. Since we cannot plug in \(x=-1\) directly, we might be interested in seeing what the (two-sided) limit is at \(x=-1\) instead. But again, we cannot directly plug in \(x=-1\) to do so.
What we can do in this case is simplify how our function is defined through factoring and fraction reduction. Notice that
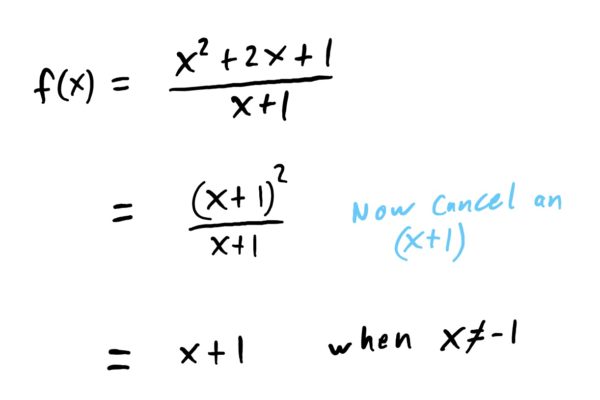
So, it turns out that this function is somewhat of a “covert” polynomial (albeit undefined at \(x=-1\) because the original version was undefined there). Now, since limits are not concerned with what is happening to a function AT EXACTLY the limit \(x\)-value (in this case, \(x=-1\)) but rather is concerned with what is happening NEARBY, we can use this reduced version of our function to find the limit! Thus
$$\begin{align} \lim_{x\rightarrow -1} \frac{x^2+2x+1}{x+1}&=\lim_{x\rightarrow -1} x+1\\&=(-1)+1\\&=0 \end{align}$$
In summary, if you cannot at first plug in a limit \(x\)-value directly, see if you can reduce or simplify the function’s definition first AND THEN plug in the limiting value.
Compute the following limits.
\(\lim_{x\rightarrow 5} 3x^2+2x+1=86\)
Since the function given is a polynomial, it is smooth, and therefore we can plug in the limit \(x\)-value \(x=5\) directly to get the limit. Replace all the \(x\)’s in the function with \(5\).
$$\begin{align}\lim_{x\rightarrow 5} 3x^2+2x+1&=3(5)^2+2\cdot(5)+1\\&=75+10+1\\&=1\end{align}$$
\(\lim_{x\rightarrow -1} 3.14x^3-2.4x^2+x-0.5\)
The function given is a polynomial, so we can compute the limit by plugging in \(x=-1\) directly. Hence,
$$\begin{align}\lim_{x\rightarrow -1} 3.14x^3-2.4x^2+x-0.5&=3.14\cdot(-1)^3-2.4\cdot(-1)^2+(-1)-0.5\\&=-3.14-2.4-1-0.5\\&=-7.04\end{align}$$
\(\lim_{x\rightarrow 2} \frac{x^2-5x+6}{x-2}=-1\)
Notice that we cannot plug in \(x=2\) directly because it would make the denominator of the function equal to zero, thereby causing a division-by-zero problem. So, in hope that we can actually compute this limit, we factor the numerator to see if we can get something to cancel the entire denominator.
The numerator factors as \(x^2-5x+6=(x-3)(x-2)\). So, we notice
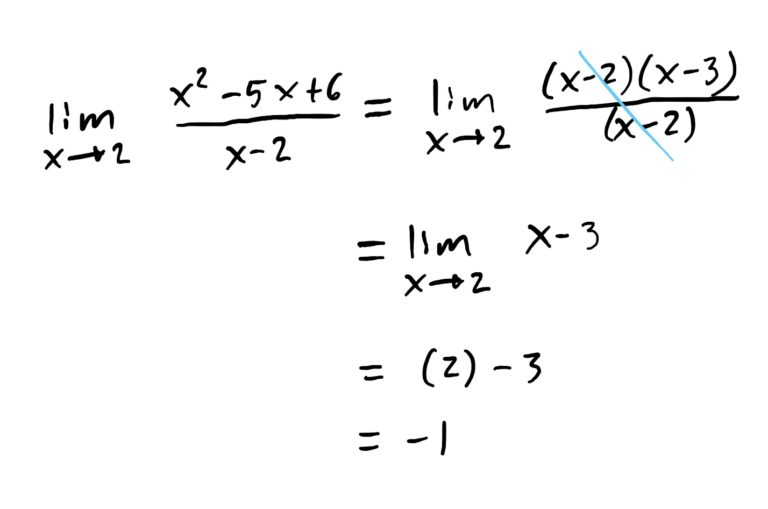
\(\lim_{x\rightarrow 1} \frac{x^2-1}{x-1}=2\)
Just like in the last problem, we cannot directly plug \(x=1\) into this function because it would make the denominator zero. So we factor the numerator (difference of squares) to get \(x^2-1=(x+1)(x-1)\). Because of this, we get some nice cancellation that allows us to compute the limit. Hence,
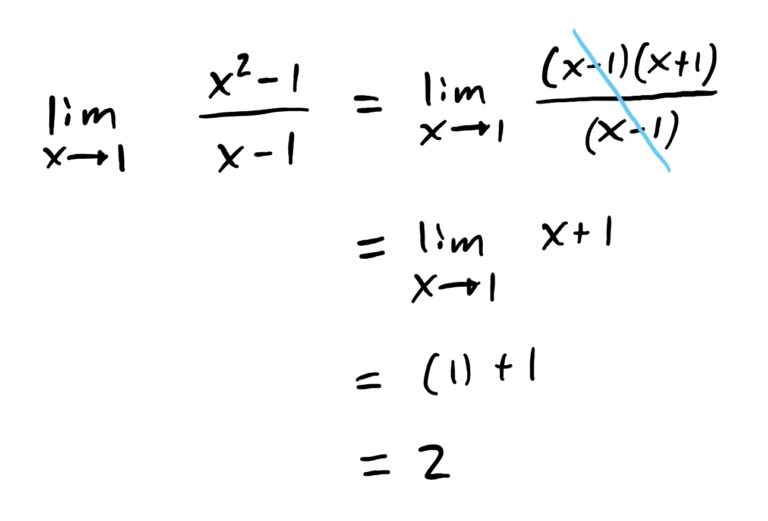
\(\lim_{h\rightarrow 0} \frac{h^2x^2+hx+4h}{h}=x+4\)
Don’t be intimidated by having two variables in this function. We are trying to find what happens to the function in the limit as the variable \(h\) goes to \(0\). We don’t care what \(x\) is at all (and so can assume it is a fixed real number).
Similar to the last problem, we can’t directly plug in \(h=0\) because the denominator will be zero. So we need to factor the top of the fraction in hope that we can cancel the \(h\) in the denominator.
The numerator can be factored as \(h^2x^2+hx+4h=h\cdot(hx^2+x+4)\). Now let’s compute the limit. Note carefully that you will be replacing \(h\) with \(0\) NOT \(x\). Leave \(x\) alone. It just comes along for the ride.
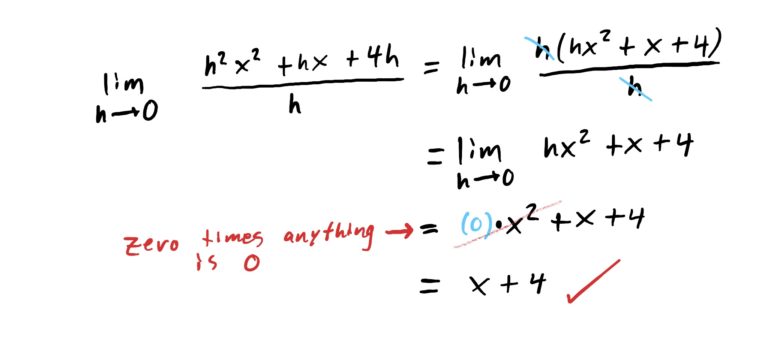
\(\lim_{h\rightarrow 0}\frac{h^3x-2h^2+h^2x^2}{h^2}=-2+x^2\)
Don’t be intimidated by having two variables in this function. We are trying to find what happens to the function in the limit as the variable \(h\) goes to \(0\). We don’t care what \(x\) is at all (and so can assume it is a fixed real number).
Similar to the last problem, we can’t directly plug in \(h=0\) because the denominator will be zero. So we need to factor the top of the fraction in hope that we can cancel the \(h\) in the denominator.
The numerator can be factored completely as \(h^3x-2h^2+h^2x^2=h^2\cdot(hx-2+x^2)\). Now let’s compute the limit. Note carefully that you will be replacing \(h\) with \(0\) NOT \(x\). Leave \(x\) alone. It just comes along for the ride.