Finding Limits Using Graphs
One and Two-Sided Limits
Let \(f\) be the function given by the graph below.
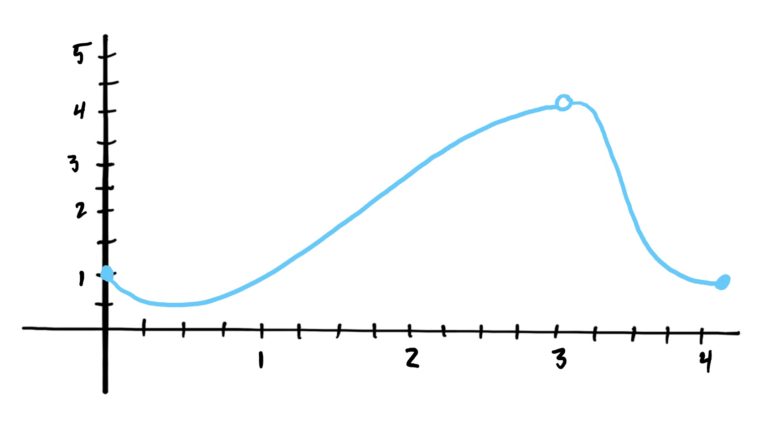
Notice that \(f\) is NOT DEFINED at \(x=3\) because there is no \(y\)-value that corresponds with \(x=3\) (the hole tells you that the graph/function is not defined wherever the open point/hole is located). However, just looking at the graph, we can tell what should be in the hole at \(x=3\).
We make this determination based on what is happening to the function’s \(y\)-values at \(x\)-values that are approaching \(x=3\) on both the left and the right of \(x=3\). We notice that as the \(x\)-values get closer to \(x=3\) on the LEFT, the corresponding \(y\)-values are getting closer to \(y=4\). Similarly, as the \(x\)-values get closer to \(x=3\) on the RIGHT, those corresponding \(y\)-values increase and get closer and closer to \(y=4\) as well. See image below.
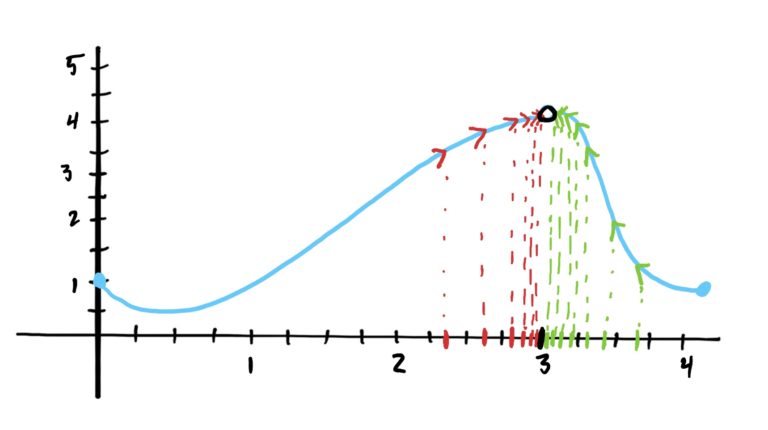
This idea is encapsulated in the following definitions.
When both one-sided limits approach the same value, we can determine a two-sided limit.
In the example above (graph given again below for convenience), we have \(\lim_{x\rightarrow 3}f(x)=4\) because we have both \(\lim_{x\rightarrow 3^+}f(x)=4\) and \(\lim_{x\rightarrow 3^-}f(x)=4\); hence the (two-sided) limit of \(f\) at \(x=3\) is \(y=4\).

Note: we don’t usually say “two-sided limit” unless it makes sense from context to do so. Normally, we simply refer to the two-sided limit of a function as just “it’s limit,” without indication of “sides.”
When a Two-Sided Limit Doesn’t Exist
Let \(g\) be the function given by the graph below.
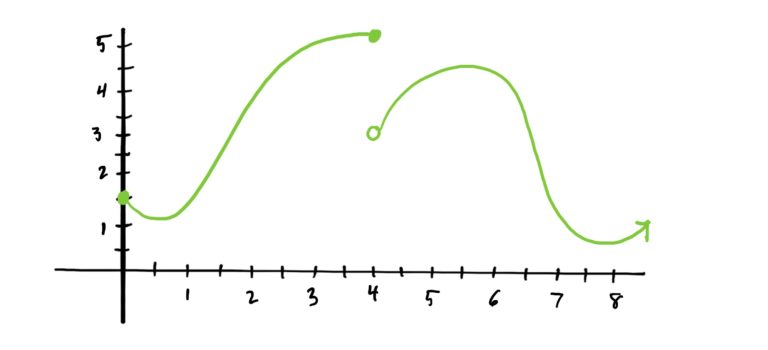
Notice that there is a “jump” in the graph at \(x=4\). Furthermore, notice that \(\lim_{x\rightarrow 4^+} g(x)=3\) whereas \(\lim_{x\rightarrow 4^-} g(x)=5\). Said verbally, the right-hand limit of \(g\) at \(x=4\) is 3, but the left-hand limit of \(g\) at \(x=4\) is 5. Since the left-hand limit and the right-hand limit are different, the two-sided limit DOES NOT EXIST! See this illustrated below.
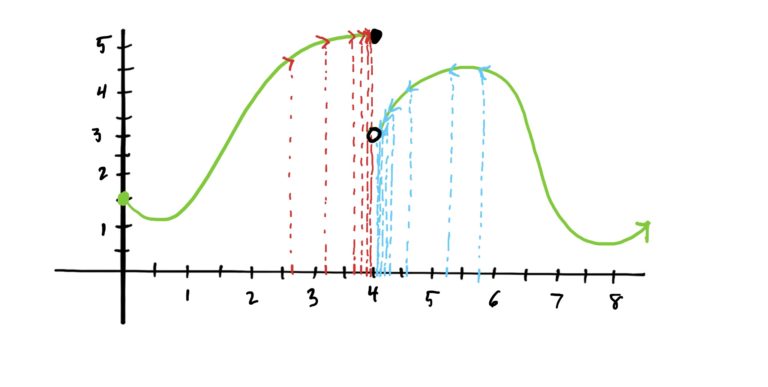
When a Limit Is Different From the Function’s Value at a Point
Occasionally, we run into the circumstance that we see in the graph below, where there is not only a hole but a point above or below the hole.
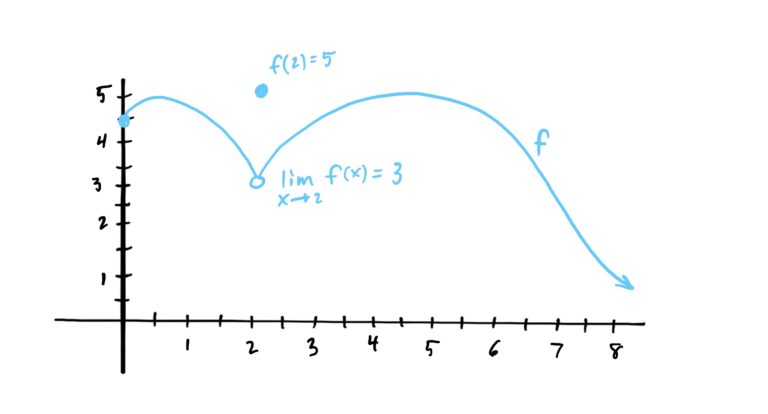
In this case, the function is defined at \(x=2\) and \(f(2)=5\), but notice that as we approach \(x=2\) from both the left and the right, we end up with a two-sided limit of \(y=3\). This illustrates that sometimes the function’s output on a specific \(x\)-value input might differ from what’s happening to the function’s outputs close by.
To express this idea mathematically, we’d write
$$\lim_{x\rightarrow 2}f(x)=3 \neq f(2)$$
- \(\lim_{x\rightarrow 1^+} f(x)\)
- \(\lim_{x\rightarrow 1^-} f(x)\)
- \(\lim_{x\rightarrow 1} f(x)\)
- \( \lim_{x\rightarrow 2}f(x)\)
- \(\lim_{x\rightarrow 3} f(x)\)
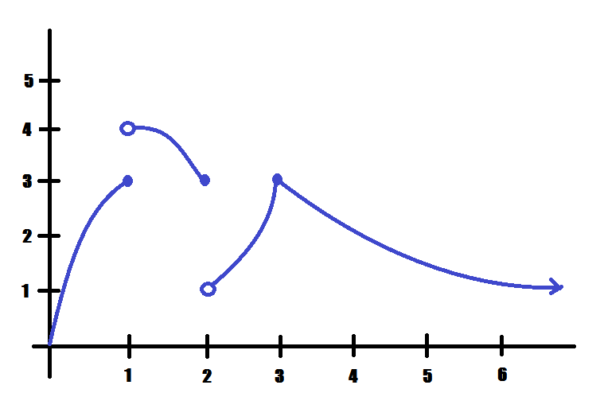
Consider what happens to the y-values of the function as you “plug in” values closer and closer to \(x=1,2\) and \(3\).
- \(\lim_{x\rightarrow 1^+} f(x)=4\)
- \(\lim_{x\rightarrow 1^-} f(x)=3\)
- \(\lim_{x\rightarrow 1} f(x)\) DNE
- \( \lim_{x\rightarrow 2}f(x)\) DNE
- \(\lim_{x\rightarrow 3} f(x)=3\)
- \(\lim_{x\rightarrow 1} f(x)\)
- \(\lim_{x\rightarrow 3} f(x)\)
- \(\lim_{x\rightarrow 4} f(x)\)
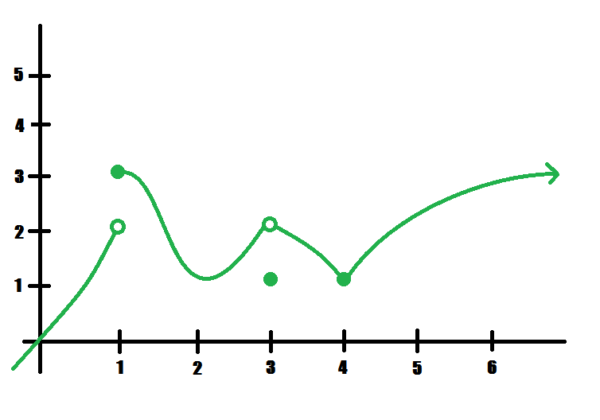
See where the y-values tend to go the closer you get to \(x=1,3\) and \(4\) on both sides of those x-values.
- \(\lim_{x\rightarrow 1} f(x)\) DNE
- \(\lim_{x\rightarrow 3} f(x)=2\)
- \(\lim_{x\rightarrow 4} f(x)=1\)
- \(\lim_{x\rightarrow 1^+} f(x)\)
- \(\lim_{x\rightarrow 2} f(x)\)
- \(\lim_{x\rightarrow 3} f(x)\)
- \(\lim_{x\rightarrow 5}f(x)\)
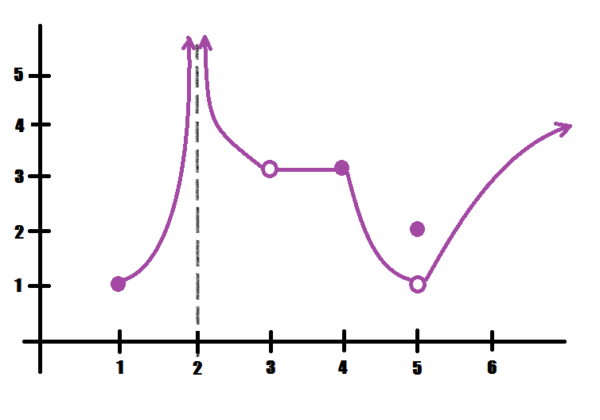
See where the y-values of the function go as you approach 1 from the right, and 2 from both sides… Note that the closer you get to 2, the bigger the y-values. Venture a guess to how big those get? For the limits approaching \(x=3\) and \(x=5\), see what happens to the y-values as you approach from both sides.
- \(\lim_{x\rightarrow 1^+} f(x)=1\)
- \(\lim_{x\rightarrow 2} f(x)=\infty\)
- \(\lim_{x\rightarrow 3} f(x)=3\)
- \(\lim_{x\rightarrow 5}f(x)=1\)
Consider the previous problems where graphs are given. Maybe one of those graphs will help with this problem.
It is possible. See video for quick reasoning as to why
Consider the previous problems where graphs are given. Maybe one of those graphs will help with this problem.
It is NOT always true. See video for quick explanation.
