Second Derivative Test for Classifying Critical Points
A Test Borne of a Simple Observation
Take a look at the graph below and locate the local mins and local maxes.
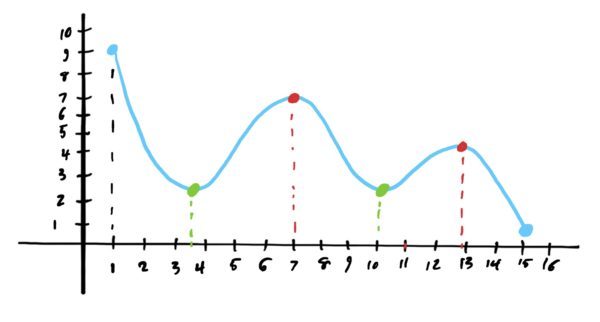
Notice that at the local maxes, the function is concave down (because its rate of change is decreasing, going from positive to negative), and at the local mins, the function is concave up (because its rate of change is increasing, changing from negative to positive). We know from a previous lesson that the concavity of a function on an interval (and at a point) can be determined by the second derivative of the function. The graph is concave down when the second derivative \(f”\) is negative. It is concave up when \(f”\) is positive. This gives us a very easy way of determining whether or not a critical point is a local min or a local max.
In a prior lesson, we found the critical points of \(f\) by finding the derivative and setting it equal to zero, then solving for \(x\). Since the point of the problem is not to find critical points but to classify them, we omit the work of finding them here. The critical points are \(x=1.1547\) and \(x=-1.1547\).
To classify these as a min or a max, simply find the second derivative of the function and plug ’em in, checking to see if the result is positive or negative. If positive, we have a min. If negative, we have a max. If zero, we need to hit it with another test.
Notice \(f^{\prime\prime}(x)=6x\) (because \(f'(x)=3x^2-4\)).
Now notice \(f^{\prime\prime}(1.1547)=6\cdot(1.1547)=6.9282\) which is positive. This indicates that the graph is concave up at \(x=1.1547\), indicating that the function has a local MINIMUM at \(x=1.1547\).
Similarly, notice \(f^{\prime\prime}(-1.1547)=-6.9282\) which is negative, indicating that \(f\) is concave down at \(x=-1.1547\), which indicates also that \(x=-1.1547\) is a local MAXIMUM.
The following diagram is useful for keeping things straight.

Start by finding the critical points of your function where \(f'(x)=0\), and plugging them into the second derivative to determine the concavity of the graph at each of those points.
- Using the 2nd Derivative Test to Classify Critical Points:
- Find critical points of \(f\):Set \(f'(x)=0\) and solve for \(x\)
- Find all \(x\)-values where \(f'(x)\) DNE
- Compute the second derivative \(f”(x)\).
- Plug each critical point \(x=c\), where \(f'(c)=0\), into \(f”(x)\) to classify them (DON’T plug in crit pts where \(f’\) DNE):If \(f”(c)>0\) then \(f\) is concave up at \(x=c\) and so \(f\) has a local min at \(x=c\). If \(f”(c)<0\), then \(f\) is concave down at \(x=c\) and so \(f\) has a local max at \(x=c\).
- If \(f”(c)=0\), the the test is inconclusive.
- Use the first derivative test, or some other means, to classify the critical points where either \(f'(x)\) DNE, or the second deriv test is inconclusive (i.e. in step 3 above).
Local Max at: \(x=\frac{1}{\sqrt{3}}\)
Local Min at: \(x=-\frac{1}{\sqrt{3}}\)
Start by finding the critical points of your function where \(f'(x)=0\), and plugging them into the second derivative to determine the concavity of the graph at each of those points.
- Using the 2nd Derivative Test to Classify Critical Points:
- Find critical points of \(f\):Set \(f'(x)=0\) and solve for \(x\)
- Find all \(x\)-values where \(f'(x)\) DNE
- Compute the second derivative \(f”(x)\).
- Plug each critical point \(x=c\), where \(f'(c)=0\), into \(f”(x)\) to classify them (DON’T plug in crit pts where \(f’\) DNE):If \(f”(c)>0\) then \(f\) is concave up at \(x=c\) and so \(f\) has a local min at \(x=c\). If \(f”(c)<0\), then \(f\) is concave down at \(x=c\) and so \(f\) has a local max at \(x=c\).
- If \(f”(c)=0\), the the test is inconclusive.
- Use the first derivative test, or some other means, to classify the critical points where either \(f'(x)\) DNE, or the second deriv test is inconclusive (i.e. in step 3 above).
Local Max at: \(x=-2\)
Local Min at: \(x=2\)
Start by finding the critical points of your function where \(f'(x)=0\), and plugging them into the second derivative to determine the concavity of the graph at each of those points.
- Using the 2nd Derivative Test to Classify Critical Points:
- Find critical points of \(f\):Set \(f'(x)=0\) and solve for \(x\)
- Find all \(x\)-values where \(f'(x)\) DNE
- Compute the second derivative \(f”(x)\).
- Plug each critical point \(x=c\), where \(f'(c)=0\), into \(f”(x)\) to classify them (DON’T plug in crit pts where \(f’\) DNE):If \(f”(c)>0\) then \(f\) is concave up at \(x=c\) and so \(f\) has a local min at \(x=c\). If \(f”(c)<0\), then \(f\) is concave down at \(x=c\) and so \(f\) has a local max at \(x=c\).
- If \(f”(c)=0\), the the test is inconclusive.
- Use the first derivative test, or some other means, to classify the critical points where either \(f'(x)\) DNE, or the second deriv test is inconclusive (i.e. in step 3 above).
Local Max at: \(-\frac{1}{\sqrt[4]{5}}\)
Local Min at: \(\frac{1}{\sqrt[4]{5}}\)
Start by finding the critical points of your function where \(f'(x)=0\), and plugging them into the second derivative to determine the concavity of the graph at each of those points.
- Using the 2nd Derivative Test to Classify Critical Points:
- Find critical points of \(f\):Set \(f'(x)=0\) and solve for \(x\)
- Find all \(x\)-values where \(f'(x)\) DNE
- Compute the second derivative \(f”(x)\).
- Plug each critical point \(x=c\), where \(f'(c)=0\), into \(f”(x)\) to classify them (DON’T plug in crit pts where \(f’\) DNE):If \(f”(c)>0\) then \(f\) is concave up at \(x=c\) and so \(f\) has a local min at \(x=c\). If \(f”(c)<0\), then \(f\) is concave down at \(x=c\) and so \(f\) has a local max at \(x=c\).
- If \(f”(c)=0\), the the test is inconclusive.
- Use the first derivative test, or some other means, to classify the critical points where either \(f'(x)\) DNE, or the second deriv test is inconclusive (i.e. in step 3 above).
Local Max at: \(x=\frac{64}{27}\)
Local Min at: \(x=0\)
Start by finding the critical points of your function where \(f'(x)=0\), and plugging them into the second derivative to determine the concavity of the graph at each of those points.
- Using the 2nd Derivative Test to Classify Critical Points:
- Find critical points of \(f\):Set \(f'(x)=0\) and solve for \(x\)
- Find all \(x\)-values where \(f'(x)\) DNE
- Compute the second derivative \(f”(x)\).
- Plug each critical point \(x=c\), where \(f'(c)=0\), into \(f”(x)\) to classify them (DON’T plug in crit pts where \(f’\) DNE):If \(f”(c)>0\) then \(f\) is concave up at \(x=c\) and so \(f\) has a local min at \(x=c\). If \(f”(c)<0\), then \(f\) is concave down at \(x=c\) and so \(f\) has a local max at \(x=c\).
- If \(f”(c)=0\), the the test is inconclusive.
- Use the first derivative test, or some other means, to classify the critical points where either \(f'(x)\) DNE, or the second deriv test is inconclusive (i.e. in step 3 above).
local min at \(x=0\).
Start by finding the critical points of your function where \(f'(x)=0\), and plugging them into the second derivative to determine the concavity of the graph at each of those points.
- Using the 2nd Derivative Test to Classify Critical Points:
- Find critical points of \(f\):Set \(f'(x)=0\) and solve for \(x\)
- Find all \(x\)-values where \(f'(x)\) DNE
- Compute the second derivative \(f”(x)\).
- Plug each critical point \(x=c\), where \(f'(c)=0\), into \(f”(x)\) to classify them (DON’T plug in crit pts where \(f’\) DNE):If \(f”(c)>0\) then \(f\) is concave up at \(x=c\) and so \(f\) has a local min at \(x=c\). If \(f”(c)<0\), then \(f\) is concave down at \(x=c\) and so \(f\) has a local max at \(x=c\).
- If \(f”(c)=0\), the the test is inconclusive.
- Use the first derivative test, or some other means, to classify the critical points where either \(f'(x)\) DNE, or the second deriv test is inconclusive (i.e. in step 3 above).
\(x=-1\) is neither a min nor a max (we were forced to use the first derivative test)
Start by finding the critical points of your function where \(f'(x)=0\), and plugging them into the second derivative to determine the concavity of the graph at each of those points.
- Using the 2nd Derivative Test to Classify Critical Points:
- Find critical points of \(f\):Set \(f'(x)=0\) and solve for \(x\)
- Find all \(x\)-values where \(f'(x)\) DNE
- Compute the second derivative \(f”(x)\).
- Plug each critical point \(x=c\), where \(f'(c)=0\), into \(f”(x)\) to classify them (DON’T plug in crit pts where \(f’\) DNE):If \(f”(c)>0\) then \(f\) is concave up at \(x=c\) and so \(f\) has a local min at \(x=c\). If \(f”(c)<0\), then \(f\) is concave down at \(x=c\) and so \(f\) has a local max at \(x=c\).
- If \(f”(c)=0\), the the test is inconclusive.
- Use the first derivative test, or some other means, to classify the critical points where either \(f'(x)\) DNE, or the second deriv test is inconclusive (i.e. in step 3 above).
Local max at \(x=0\)
local min at \(x=4\)
