Recall that we said a function is concave up on an interval provided that the slopes of the graph inside that interval are increasing, and that the graph is concave down on an interval provided that the slopes are decreasing. Concavity indicates how quickly the function is increasing or decreasing. Concave up indicates that the graph is rapidly increasing (or decreasing less quickly) and concave down indicates that the graph is decreasing more quickly (or increasing more slowly). This is depicted in the graph below.
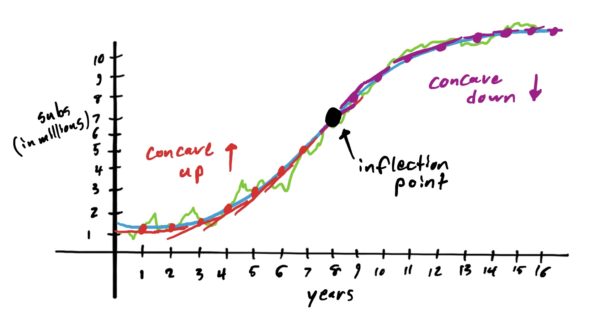
Note that we also mentioned in the previous lesson that because concavity direction indicates the rate of change of the rate of change (i.e. how quickly the graph is increasing or decreasing), we can determine a graph’s concavity by its second derivative.
Recall that we call the transition point x=c where the concavity of the function changes an inflection point. Moreover, because it’s a transition point, the function is neither concave up nor down at that point, making f”(c)=0 or f”(x) undefined. This gives us a neat way of determining where a function is concave up or down that is especially useful for polynomials and other sufficiently well-behaved functions.
Note that the above method doesn’t handle the case where f is neither concave up nor down on an entire interval. If you are dealing with a function of this type, you would find that the function’s second derivative is zero on an entire interval as opposed to a handful of individual points when trying to find all inflection points. This is a weird case that we won’t consider here in any of our examples.
Note also that we are able to determine the concavity of an entire interval (between potential inflection points) because when we find our potential inflection points by setting f”(x)=0 we have found all possible places where the function could change concavity. Put another way, if we suppose the function changed concavity between inflection points, then there would be another inflection point aside from the ones we already found… but that’s not possible because we had found them all! So the concavity must be the same between and beyond all inflection points.
Following the procedure above, we first find all possible inflection points by deriving the function twice and setting it to zero and solving for x, and also determining where the second derivative is undefined. The work for this is shown below:

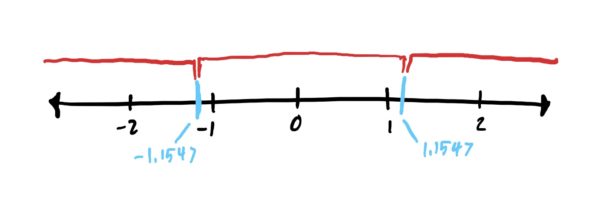
By the above, we see that the potential inflection points are x=1.1547 and x=-1.1547. Note that since f” is a polynomial, there is nowhere where f” can be undefined.
So, now we build a number line and plot these x-values, and divide up the number line into subintervals, which we will demarcate in red:
Now, on each of these red intervals we choose our favorite x-values and plug them into f”. If f”(x)>0 then f is concave up on that interval. If f”(x)<0, then f is concave down on that interval. I chose to plug in x=-2 for the first interval, x=0 for the second, and x=2 for the third. Your choice could have been very different. Computations are shown below, with an up or down arrow (you could use “+” or “-” instead) on each interval to express whether f is concave up or down. Viz:
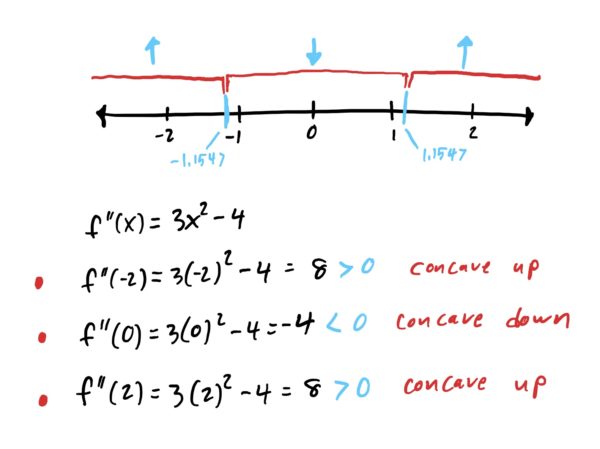
Lastly, we want to find our inflection points. This is easy: at each potential inflection point determine if the concavity is different before and after it. Looking at x=-1.1547 the concavity changed from concave up to concave down, reading the number line from left to right. Similarly, at x=1.1547 the concavity changed from concave down to concave up. Therefore, both of our potential inflection points are actual inflection points.
In summary, we have that our function f is concave up from -\infty up to x=1.15, and from x=1.1547 to \infty, and concave down between x=-1.1547 and x=1.1547. The inflection points are x=-1.1547 and x=1.1547 (because the concavity changes at each).
First, find potential inflection points by finding where the second derivative is equal to zero or is undefined.
First, find potential inflection points by finding where the second derivative is equal to zero or is undefined.
First, find potential inflection points by finding where the second derivative is equal to zero or is undefined.
First, find potential inflection points by finding where the second derivative is equal to zero or is undefined.
First, find potential inflection points by finding where the second derivative is equal to zero or is undefined.
