Quotient Rule
Deriving Fractions of Functions
In the previous lesson, we have discussed how to derive products of functions, or functions that are multiplied together. How do we go about deriving fractions of functions, or functions that are being divided? We use the Quotient Rule, which is very similar to the product rule, but with an extra complication.
Put into words,
$$\left(\frac{f(x)}{g(x)}\right)’=\frac{(derive\ f)(copypaste\ g)-(copypaste\ f)(derive\ g)}{g\ squared}$$
Notice that the numerator is basically the same as what you’d get for the product rule EXCEPT that we are subtracting instead of adding. We also have that \(g(x)\) squared in the denom. So its not too much extra to memorize.
First, we will let \(f(x)=x^2\) and \(g(x)=x^3+2\). Then, the derivative can be found by substitution as shown below.
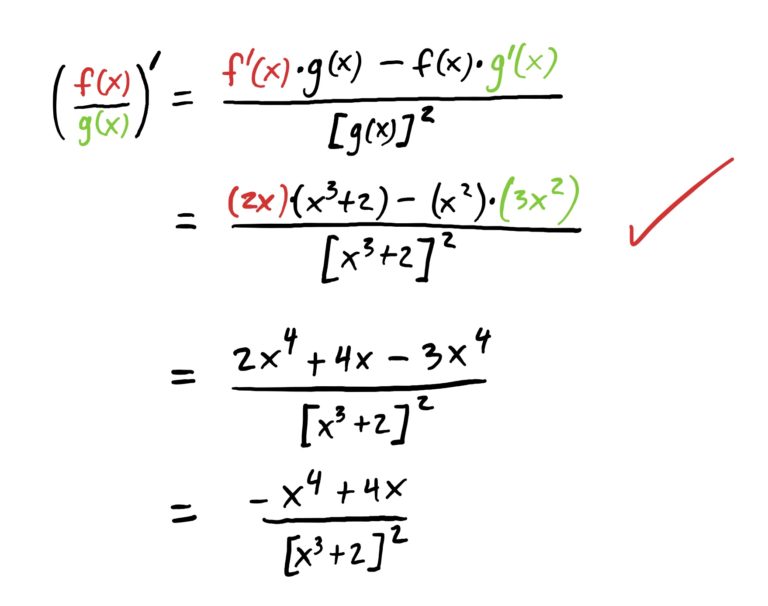
Finding Tangent Lines Using the Quotient Rule
Finding tangent lines using the quotient rule works exactly the same as how we do it with any other derivative rule. Nothing changes at all… except the rule we use to find the slope of the tangent line. See example below.
Remember: to find the equation of a tangent line using the point-slope formula for lines \((y-y_0)=m(x-x_0)\), we need three ingredients: \(m\) which is the slope of the line, which can be found from the derivative of your function at the given \(x\)-value, and the \(x\) and \(y\)-value of a point on your line, which we get from the \(x\)-value given, and the \(y\)-value of the function \(H\) at \(x=1\).
To find the slope, we need to find the derivative of \(H\). This was done in the example above. We found that
$$H'(x)=\frac{(2x)(x^3+2)-(x^2)(3x^2)}{[x^3+2]}$$
To see the steps for how it was computed, expand the dropdown box below.
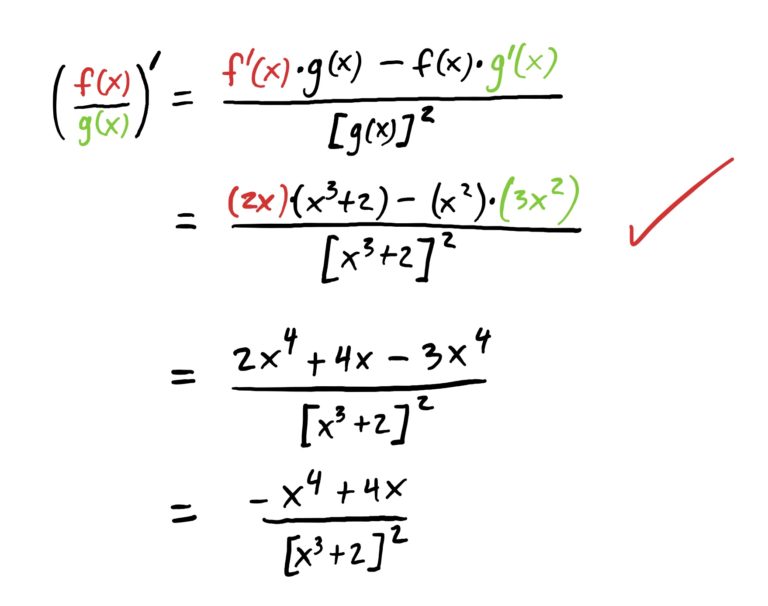
Now, to find \(m\), we need only plug \(x=1\) into \(H'(x)\). This gives us
$$\begin{align}H'(1)&=\frac{(2\cdot(1))((1)^3+2)-((1)^2)(3\cdot(1)^2)}{[(1)^3+2]}\\&=\frac{3}{3}\\&=1\end{align}$$
So we have \(m=1\). Also, we are given the \(x\)-value of the point on the line, namely \(x=1\). We still need a \(y\)-value. This we get by plugging \(x=1\) into \(H\) (NOT \(H’\)). This gives us
$$H(1)=\frac{(1)^2}{(1)^3+2}=\frac{1}{3}$$
So, in summary, we have \(m=1\), \(x_0=1\), and \(y_0=\frac{1}{3}\). Now let’s plug this into the point-slope formula for lines: \((y-y_0)=m(x-x_0)\). This gives us
$$(y-\frac{1}{3})=1\cdot(x-1)$$
When you solve for \(y\), you get the equation of the tangent line
$$y=x-\frac{2}{3}$$.
Done!
Use the Quotient Rule to find the following derivatives
\(\frac{d}{dx} \frac{f(x)}{g(x)}=\frac{(derive\ top)\cdot(bottom)-(top)\cdot(derive bottom)}{(bottom)^2}\)
Quotient Rule: \(\frac{d}{dx}\frac{f(x)}{g(x)}=\frac{f'(x)g(x)-f(x)g'(x)}{[g(x)]^2}\)
\(\frac{d}{dx} \frac{f(x)}{g(x)}=\frac{(derive\ top)\cdot(bottom)-(top)\cdot(derive bottom)}{(bottom)^2}\)
\(f'(x)=\frac{-5}{(3x-1)^2}\)
\(\frac{d}{dx} \frac{f(x)}{g(x)}=\frac{(derive\ top)\cdot(bottom)-(top)\cdot(derive bottom)}{(bottom)^2}\)
Quotient Rule: \(\frac{d}{dx}\frac{f(x)}{g(x)}=\frac{f'(x)g(x)-f(x)g'(x)}{[g(x)]^2}\)
\(\frac{d}{dx} \frac{f(x)}{g(x)}=\frac{(derive\ top)\cdot(bottom)-(top)\cdot(derive bottom)}{(bottom)^2}\)
\(f'(x)=\frac{4x}{(x^2+1)^2}\)
\(\frac{d}{dx} \frac{f(x)}{g(x)}=\frac{(derive\ top)\cdot(bottom)-(top)\cdot(derive bottom)}{(bottom)^2}\)
Quotient Rule: \(\frac{d}{dx}\frac{f(x)}{g(x)}=\frac{f'(x)g(x)-f(x)g'(x)}{[g(x)]^2}\)
\(\frac{d}{dx} \frac{f(x)}{g(x)}=\frac{(derive\ top)\cdot(bottom)-(top)\cdot(derive bottom)}{(bottom)^2}\)
\(f'(x)=\frac{3.1x^2-5x+15.5}{(x^2-5)^2}\)
\(\frac{d}{dx} \frac{f(x)}{g(x)}=\frac{(derive\ top)\cdot(bottom)-(top)\cdot(derive bottom)}{(bottom)^2}\)
\(\frac{d}{dx} \frac{f(x)}{g(x)}=\frac{(derive\ top)\cdot(bottom)-(top)\cdot(derive bottom)}{(bottom)^2}\)
Quotient Rule: \(\frac{d}{dx}\frac{f(x)}{g(x)}=\frac{f'(x)g(x)-f(x)g'(x)}{[g(x)]^2}\)
\(f'(x)=\frac{(\frac{1}{3}x^{\frac{-2}{3}}+2x^{-3})(x^{\frac{1}{2}}+x^3)-(x^\frac{1}{3}-x^{-2})(\frac{1}{2}x^{\frac{-1}{2}}+3x^2)}{(x^{\frac{1}{2}}+x^3)^2}\)
\(\frac{d}{dx} \frac{f(x)}{g(x)}=\frac{(derive\ top)\cdot(bottom)-(top)\cdot(derive bottom)}{(bottom)^2}\)
\(\frac{d}{dx} \frac{f(x)}{g(x)}=\frac{(derive\ top)\cdot(bottom)-(top)\cdot(derive bottom)}{(bottom)^2}\)
Quotient Rule: \(\frac{d}{dx}\frac{f(x)}{g(x)}=\frac{f'(x)g(x)-f(x)g'(x)}{[g(x)]^2}\)
\(f'(x)=\frac{(x^{-\frac{2}{3}}+2x)(x^{-2}-x^{-3})-(3x^{\frac{1}{3}}+x^2)(2x^{-3}+3x^{-4})}{(x^{-2}-x^{-3})^2}\)
First convert radicals to fractional powers, then use \(\frac{d}{dx} \frac{f(x)}{g(x)}=\frac{(derive\ top)\cdot(bottom)-(top)\cdot(derive bottom)}{(bottom)^2}\)
\(\frac{d}{dx} \frac{f(x)}{g(x)}=\frac{(derive\ top)\cdot(bottom)-(top)\cdot(derive bottom)}{(bottom)^2}\)
Quotient Rule: \(\frac{d}{dx}\frac{f(x)}{g(x)}=\frac{f'(x)g(x)-f(x)g'(x)}{[g(x)]^2}\)
\(f'(x)=\frac{(2x^{-\frac{1}{2}})(x^2-x^{1}{3})-(4x^{\frac{1}{2}}+3)(2x-\frac{1}{3}x^{\frac{-2}{3}})}{(x^2-x^{\frac{1}{3}})^2}\)
\(\frac{d}{dx} \frac{f(x)}{g(x)}=\frac{(derive\ top)\cdot(bottom)-(top)\cdot(derive bottom)}{(bottom)^2}\), note that the derivative of \(e^x\) is itself.
\(\frac{d}{dx} \frac{f(x)}{g(x)}=\frac{(derive\ top)\cdot(bottom)-(top)\cdot(derive bottom)}{(bottom)^2}\)
Quotient Rule: \(\frac{d}{dx}\frac{f(x)}{g(x)}=\frac{f'(x)g(x)-f(x)g'(x)}{[g(x)]^2}\)
\(f'(x)=\frac{e^{x}(x-1)}{x^2}\)
First convert radicals to fractional powers, then powers of x up to numerators of the little fractions. Then hit it with \(\frac{d}{dx} \frac{f(x)}{g(x)}=\frac{(derive\ top)\cdot(bottom)-(top)\cdot(derive bottom)}{(bottom)^2}\)
\(\frac{d}{dx} \frac{f(x)}{g(x)}=\frac{(derive\ top)\cdot(bottom)-(top)\cdot(derive bottom)}{(bottom)^2}\)
Quotient Rule: \(\frac{d}{dx}\frac{f(x)}{g(x)}=\frac{f'(x)g(x)-f(x)g'(x)}{[g(x)]^2}\)
\(f'(x)=\frac{(-8x^{-3}+6x^{-4})(x^{-\frac{1}{2}}+1)-(4x^{-2}-2x^{-3})(-\frac{1}{2}x^{-\frac{3}{2}})}{(x^{-\frac{1}{2}}+1)^2)}\)
Foil first, then use \(\frac{d}{dx} \frac{f(x)}{g(x)}=\frac{(derive\ top)\cdot(bottom)-(top)\cdot(derive bottom)}{(bottom)^2}\)
\(\frac{d}{dx} \frac{f(x)}{g(x)}=\frac{(derive\ top)\cdot(bottom)-(top)\cdot(derive bottom)}{(bottom)^2}\)
Quotient Rule: \(\frac{d}{dx}\frac{f(x)}{g(x)}=\frac{f'(x)g(x)-f(x)g'(x)}{[g(x)]^2}\)
\(f'(x)=\frac{(2x+2)(x^2-2x+1)-(x^2+2x+1)(2x-2)}{(x^2-2x+1)^2}\)
First convert radicals to fractional powers, then powers of x up to numerators of the little fractions. Then hit it with \(\frac{d}{dx} \frac{f(x)}{g(x)}=\frac{(derive\ top)\cdot(bottom)-(top)\cdot(derive bottom)}{(bottom)^2}\)
\(\frac{d}{dx} \frac{f(x)}{g(x)}=\frac{(derive\ top)\cdot(bottom)-(top)\cdot(derive bottom)}{(bottom)^2}\)
Quotient Rule: \(\frac{d}{dx}\frac{f(x)}{g(x)}=\frac{f'(x)g(x)-f(x)g'(x)}{[g(x)]^2}\)
\(f'(x)=\frac{(\frac{1}{2}x^{-\frac{1}{2}}+2x^{-3})(1+x^{-\frac{1}{3}})-(x^{\frac{1}{2}}-x^{-2})(-\frac{1}{3}x^{-\frac{4}{3}})}{(1+x^{-\frac{1}{3}})^2}\)
Find common denominator in the big fraction numerator. Get things to just one fraction, then hit it with \(\frac{d}{dx} \frac{f(x)}{g(x)}=\frac{(derive\ top)\cdot(bottom)-(top)\cdot(derive bottom)}{(bottom)^2}\)
\(\frac{d}{dx} \frac{f(x)}{g(x)}=\frac{(derive\ top)\cdot(bottom)-(top)\cdot(derive bottom)}{(bottom)^2}\)
Quotient Rule: \(\frac{d}{dx}\frac{f(x)}{g(x)}=\frac{f'(x)g(x)-f(x)g'(x)}{[g(x)]^2}\)
\(f'(x)=\frac{(1+2x)(x^{\frac{3}{2}}+5x-x^{\frac{1}{2}}-5)-(x+x^2)(\frac{3}{2}x^{\frac{1}{2}}+5-\frac{1}{2}x^{-\frac{1}{2}})}{(x^{\frac{3}{2}}+5x-x^{\frac{1}{2}}-5)^2}\)
Simplify the fraction first so you only have one big fraction. Then use \(\frac{d}{dx} \frac{f(x)}{g(x)}=\frac{(derive\ top)\cdot(bottom)-(top)\cdot(derive bottom)}{(bottom)^2}\)
\(\frac{d}{dx} \frac{f(x)}{g(x)}=\frac{(derive\ top)\cdot(bottom)-(top)\cdot(derive bottom)}{(bottom)^2}\)
Quotient Rule: \(\frac{d}{dx}\frac{f(x)}{g(x)}=\frac{f'(x)g(x)-f(x)g'(x)}{[g(x)]^2}\)
\(f'(x)=\frac{(2x)(x^2+3+x^3+3x)-x^2\cdot(2x+3x^2+3)}{(x^2+3+x^3+3x)^2}\)
For each of the following functions, find the tangent at the given point.
First find the derivative of \(f\) using the quotient rule to find the slope \(m\) of the tangent line.
- Find \(y_0=f(x_0)\), i.e. the y-value of the given x-value (if not provided already)
- Compute f'(x)
- Compute m=f'(x_0), i.e. plug in given x-value into derivative found in step 2.
- Plug \(x_0,y_0,m\) into point-slope formula \(y-y_0)=m\cdot(x-x_0)\) and solve for \(y\).
- Point-Slope Form: \((y-y_0)=m\cdot(x-x_0)\)
- Quotient Rule: \(\frac{d}{dx}\frac{f(x)}{g(x)}=\frac{f'(x)g(x)-f(x)g'(x)}{[g(x)]^2}\)
\(y=x-1\)
First find the derivative of \(f\) using the quotient rule to find the slope \(m\) of the tangent line.
- Point-Slope Form: \((y-y_0)=m\cdot(x-x_0)\)
- Quotient Rule: \(\frac{d}{dx}\frac{f(x)}{g(x)}=\frac{f'(x)g(x)-f(x)g'(x)}{[g(x)]^2}\)
- Find \(y_0=f(x_0)\), i.e. the y-value of the given x-value (if not provided already)
- Compute f'(x)
- Compute m=f'(x_0), i.e. plug in given x-value into derivative found in step 2.
- Plug \(x_0,y_0,m\) into point-slope formula \(y-y_0)=m\cdot(x-x_0)\) and solve for \(y\).
\(y=\frac{-13}{36}x+\frac{25}{36}\)
First find the y-value of the point on the tangent line by calculating \(f(2)\). Then find the slope of the tangent line \(m\), using the quotient rule.
- Point-Slope Form: \((y-y_0)=m\cdot(x-x_0)\)
- Quotient Rule: \(\frac{d}{dx}\frac{f(x)}{g(x)}=\frac{f'(x)g(x)-f(x)g'(x)}{[g(x)]^2}\)
- Find \(y_0=f(x_0)\), i.e. the y-value of the given x-value (if not provided already)
- Compute f'(x)
- Compute m=f'(x_0), i.e. plug in given x-value into derivative found in step 2.
- Plug \(x_0,y_0,m\) into point-slope formula \(y-y_0)=m\cdot(x-x_0)\) and solve for \(y\).
\(y=\frac{e^2}{4}\)
