$Project Greater Ed Logo$

Derivatives of Logarithmic Functions

Business Calculus Basic Derivative Rules Derivatives of Logarithmic Functions

Finding the Derivative of $\ln(x)$

Let’s investigate how one can derive $ln(x)$. Recall that exponentials cancel logs and vice-versa. Specifically, when $x>0$, note:

$$e^{\ln(x)}=x$$

because the exponential cancels the log. Now, if our goal is to find $\frac{d}{dx} \ln(x)$ we can compute it using what we already know about derivatives and also a little bit of algebra on the above equation. See steps below!

cancelling the e^ln(x) to get x in front of the derivative (yet to be found) of ln(x)

The Derivative of $ln(x)$

For all $x>0$,
$$\frac{d}{dx} \ln(x)=\frac{1}{x}

Deriving Logs with Stuff Inside

The above formula for the derivative of $ln(x)$ also gives us a neat formula for computing derivatives of logs with (nontrivial) functions inside them if we employ the chain-rule.

The Derivative of $ln(g(x))$

Let $g$ be a function whose $y$-values are always positive and whose derivative exists for all $x$-values in its domain. Then
$$\frac{d}{dx}\ln(g(x))=\frac{g'(x)}{g(x)}$$

As mentioned before, this rule comes entirely from the chain rule and the derivative of natural logs. The numerator in the rule above comes from multiplying by the derivative $g’$ of the inside function $g$, and the $g(x)$ in the denominator is the original inside function that replaces $x$ in the rule $\frac{d}{dx}\ln(x)=\frac{1}{x}$.

Below is an example of how this log-chain-rule thing works in practice.

One can either use the chain rule idea here, or just use the formula. We will just use the formula. Find the derivative of the inside and put on top. Copy-paste the inside and put it in the denominator. That easy. Be below.

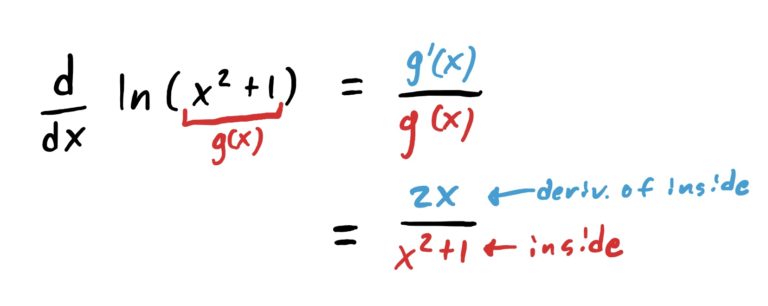
computing the derivative of the given function by putting the derivative of inside on top and original inside on bottom.

Deriving Non-Natural Logs

We can use the above rule to derive non-natural logs with stuff inside, like $\log_2(x^3+2x-1)$. Here the base is $2$ instead of $e$. Thankfully, this doesn’t complicate things too much. We just hit it with the change-of-base formula.

Deriving $\log_a{g(x)}$

Let $g$ be a function whose $y$-values are always positive and whose derivative exists for all $x$-values in its domain and let $a$ be a positive real number. Then
$$\log_a{g(x)}=\frac{\ln(g(x))}{\ln(a)}$$
Which thus implies
$$\begin{align}\frac{d}{dx}\log_a(g(x))&=\frac{d}{dx}\frac{\ln(g(x))}{ln(a)}\\&=\frac{1}{\ln(a)}\cdot\frac{g'(x)}{g(x)}\end{align}$$

In other words, we first use the change of base formula to convert the log to the natural log (which we know how to derive), noting that $\ln(a)$ is just an ugly number that we more or less just carry along for the ride, and derive the natural log part as usual. All of this is demonstrated in the quick example below.

First we convert this log to a fraction of natural logs using the change-of-base formula.

$$\begin{align}\log_2(x^3+x^2-1)&=\frac{\ln(x^3+x^2-1)}{\ln(2)}\end{align}$$

Note that $\ln(2)$ is just an ugly number. In fact, if it’s helpful to compute it’s decimal value (approximately), then do so. $ln(2)=0.693147$. So we can now rewrite the above as

$$\begin{align}\frac{\ln(x^3+x^2-1)}{\ln(2)}&=\frac{\ln(x^3+x^2-1)}{0.693147}\\&=\frac{1}{0.693147}\cdot\ln(x^3+x^2-1)\\&=1.1442695\cdot \ln(x^3+x^2-1)\end{align}$$

Now we can take derivatives as usual using our rule for deriving logs, just carrying along that constant out in front until the end of the problem.

$$\begin{align}\frac{d}{dx}1.1442695\cdot \ln(x^3+x^2-1)&=1.1442695\cdot \frac{d}{dx} \ln(x^3+x^2-1)\\&=1.1442695 \frac{3x^2+2x}{x^3+x^2-1}\end{align}$$

Now, you can leave the answer as you see it above, or you can distribute that nasty decimal through the numerator. Up to you.

Again, the method is: convert the “unnatural” log using change-of-base, then derive it as usual.

Use the formula $\frac{d}{dx}\ln(g(x))=\frac{g'(x)}{g(x)}$

For deriving natural logarithmic functions $\ln(g(x))$:

copy/paste the inside of the log into the bottom of a fraction
Derive the function inside the log and put it in the numerator of the fraction

Derivative of Natural Logs: $\frac{d}{dx}\ln(g(x))=\frac{g'(x)}{g(x)}$

$\frac{d}{dx}\ln(x^2)=\frac{2}{x}$

Use the formula $\frac{d}{dx}\ln(g(x))=\frac{g'(x)}{g(x)}$

For deriving natural logarithmic functions $\ln(g(x))$:

copy/paste the inside of the log into the bottom of a fraction
Derive the function inside the log and put it in the numerator of the fraction

Derivative of Natural Logs: $\frac{d}{dx}\ln(g(x))=\frac{g'(x)}{g(x)}$

$\frac{d}{dx} \ln(5x+3)=\frac{5}{5x+3}$

First write the radical as a fractional power, then apply the method used for deriving logs

For deriving natural logarithmic functions $\ln(g(x))$:

copy/paste the inside of the log into the bottom of a fraction
Derive the function inside the log and put it in the numerator of the fraction

Derivative of Natural Logs: $\frac{d}{dx}\ln(g(x))=\frac{g'(x)}{g(x)}$

$\frac{d}{dx}\ln(\sqrt{x})=\frac{1}{2x}$

Use change of base formula

First apply Change-of-Base formula so you only have natural logs.
Use the formula $\frac{d}{dx} \ln(g(x))=\frac{g'(x)}{g(x)}$ to derive logarithmic functions, either directly, or along with other derivative rules (i.e. product, chain, quotient). Treat logs of numbers as constants and not functions.

Derivative of Natural Logs: $\frac{d}{dx}\ln(g(x))=\frac{g'(x)}{g(x)}$
Change-of-Base Formula: $\log_b(a)=\frac{\ln(a)}{\ln(b)}$

$\frac{d}{dx} \log_2(x)=\frac{1}{x\ln(2)}$

Use change of base formula

First apply Change-of-Base formula so you only have natural logs.
Use the formula $\frac{d}{dx} \ln(g(x))=\frac{g'(x)}{g(x)}$ to derive logarithmic functions, either directly, or along with other derivative rules (i.e. product, chain, quotient). Treat logs of numbers as constants and not functions.

Derivative of Natural Logs: $\frac{d}{dx}\ln(g(x))=\frac{g'(x)}{g(x)}$
Change-of-Base Formula: $\log_b(a)=\frac{\ln(a)}{\ln(b)}$

$\frac{d}{dx} \log_3(x^2+1)=\frac{2x}{(x^2+1)\ln(3)}$

Previous Topic

Back to Lesson

Next Lesson

Business Calculus

Derivatives of Logarithmic Functions

Finding the Derivative of \(\ln(x)\)

$$e^{\ln(x)}=x$$

The Derivative of \(ln(x)\)

Deriving Logs with Stuff Inside

The Derivative of \(ln(g(x))\)

Deriving Non-Natural Logs

Deriving \(\log_a{g(x)}\)

$$\begin{align}\frac{\ln(x^3+x^2-1)}{\ln(2)}&=\frac{\ln(x^3+x^2-1)}{0.693147}\\&=\frac{1}{0.693147}\cdot\ln(x^3+x^2-1)\\&=1.1442695\cdot \ln(x^3+x^2-1)\end{align}$$