Finding Derivatives Using Several Different Rules
Identifying the “Outermost Operation”
More often than not, when we are given modestly complicated functions to derive, said functions require that multiple derivative rules be used sequentially. To determine which derivative rule we need to use first we determine which operation (multiplication, division, or composition) is the “outermost” operation. Let’s take a look at the function \(f(x)\) below:
$$f(x)=x^2\cdot \ln(x^3+2x+1)$$
Looking at this carefully, we have two functions being multiplied, namely \(x^2\) and \(\ln(x^3+2x+1)\) which warrants use of the product rule. We also have function composition, with \(x^3+2x+1\) being plugged into \(\ln(x)\) to get \(\ln(x^3+2x+1)\), which requires use of the chain rule. So which rule do we use first? It turns out we would use the product rule first because it is the “outermost” operation. The composition \(\ln(x^3+2x+1)\) is “contained within” the product \(x^2\cdot \ln(x^3+2x+1)\).
Looking at another example,
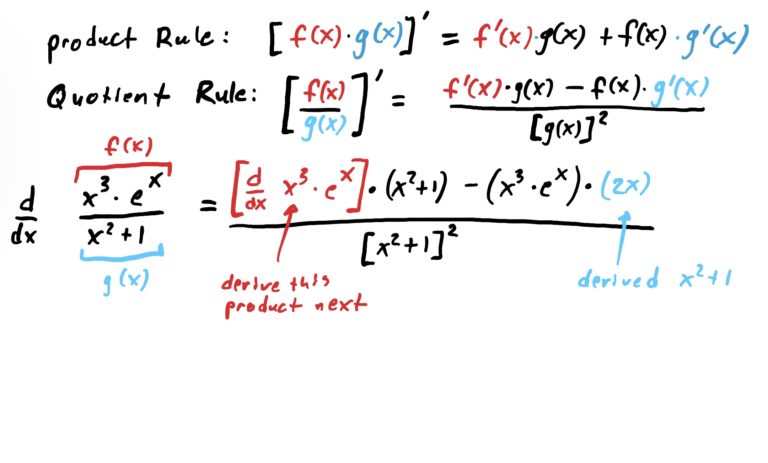
$$g(x)=\frac{x^3\cdot e^x}{x^2+1}$$
We would use the quotient rule first because the product \(x^3\cdot e^x\) is “contained within” the fraction (specifically, it is the numerator of the fraction containing it).
Last example. Let
$$h(x)=\ln\left(\frac{x^2-1}{x^2+1}\right)$$
To derive \(h\), we would start by using the chain rule because the fraction is contained within another function, namely the log. So the “outermost operation” is function composition (which warrants the chain rule).
So, to determine which operation is the “outermost operation, ” ask yourself which type of situation your function most closely resembles:
| Function Structure / Outermost Operation | Derivative Rule to Start With |
| \(f(x)\cdot g(x)\) | Product Rule |
| \(\frac{f(x)}{g(x)}\) | Quotient Rule |
| \(f(g(x))\) | Chain Rule |
Overall, it will likely take some experience with deriving functions requiring multiple rules to build up some intuition as to what rule to use first.
Now that we’ve discussed identifying the derivative rule to use first, we should probably go through how to actually compute derivatives using multiple rules.
Deriving Functions Using Multiple Rules
Let’s work through the examples presented above
Which form from the table above does this function take? What is the outermost operation? Multiplication of functions is the answer. Let \(f(x)=x^2\) and \(g(x)=\ln(x^3+2x+1)\). Notice that the operation in \(g\) is function composition, with \(x^3+2x+1\) being “plugged into ” \(\ln(x)\). That will require the chain rule. See how this all works out below.
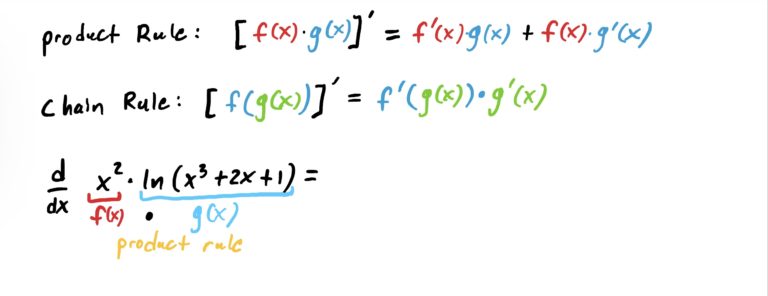
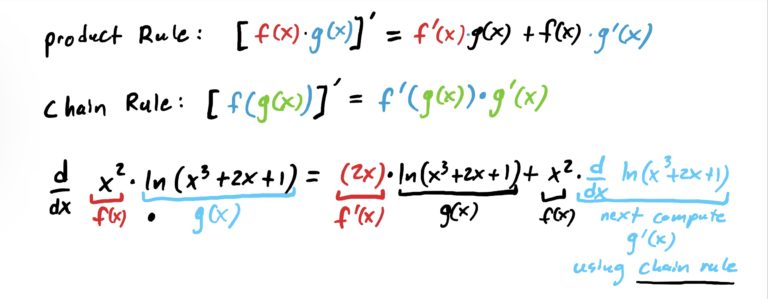
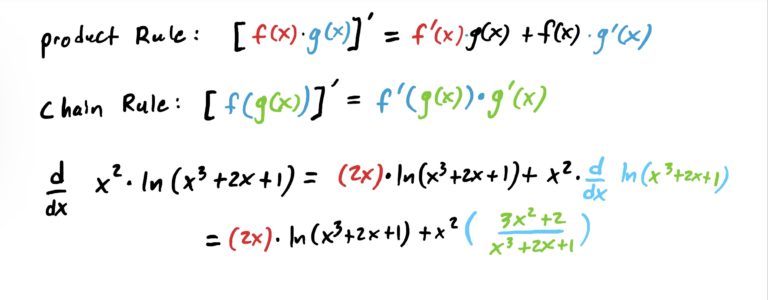
Notice that we first derived the product \(x^2\) times \(\ln(x^3+2x+1)\), but to compute the derivative of \(\ln(x^3+2x+1)\) as part of the product rule we need to use the chain rule (or just the rule for logs with stuff inside). This is shown in the last line above in green.
If you wanted to, you can simplify the above. The problem didn’t ask us to, so we wont.
As mentioned before, the outermost operation is division. There is a product \(x^3\cdot e^x\) in the numerator, but this product is contained in the quotient (because it’s the numerator). So we start by using the quotient rule. Along the way, in deriving the numerator, we will need to use the product rule. This is shown in the steps below.
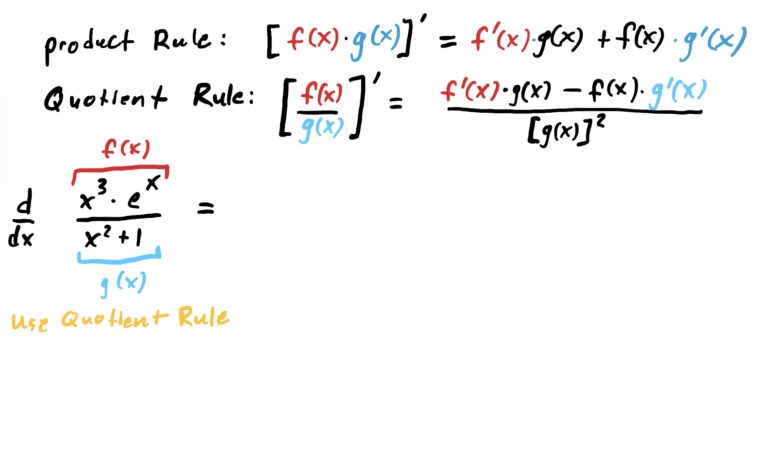

It is STRONGLY advised that you try some of the examples below yourself before looking at the solutions. Don’t touch any homework problems until you have done so!
Find the following derivatives.
Start with Product Rule, followed by Chain Rule
- Product Rule: \(\frac{d}{dx}f(x)\cdot g(x)=f'(x)g(x)+f(x)g'(x)\)
- Quotient Rule: \(\frac{d}{dx} \frac{f(x)}{g(x)} = \frac{f'(x)g(x)-f(x)g'(x)}{[g(x)]^2}\)
- Chain Rule: \(\frac{d}{dx}f(g(x))=f'(g(x))\cdot g'(x)\)
- Exponential Derivatives: \(\frac{d}{dx}e^{g(x)}=e^{g(x)}\cdot g'(x)\)
\(e^{x^2+1}\cdot [1+2x^2]\) (after a bit of simplifying)
Start with Product Rule, followed by Chain Rule
- Product Rule: \(\frac{d}{dx}f(x)\cdot g(x)=f'(x)g(x)+f(x)g'(x)\)
- Quotient Rule: \(\frac{d}{dx} \frac{f(x)}{g(x)} = \frac{f'(x)g(x)-f(x)g'(x)}{[g(x)]^2}\)
- Chain Rule: \(\frac{d}{dx}f(g(x))=f'(g(x))\cdot g'(x)\)
- Exponential Derivatives: \(\frac{d}{dx}e^{g(x)}=e^{g(x)}\cdot g'(x)\)
\(e^{-1}[1-x]+3e^{3x}\)
Start with Product Rule, followed by Chain Rule
- Product Rule: \(\frac{d}{dx}f(x)\cdot g(x)=f'(x)g(x)+f(x)g'(x)\)
- Quotient Rule: \(\frac{d}{dx} \frac{f(x)}{g(x)} = \frac{f'(x)g(x)-f(x)g'(x)}{[g(x)]^2}\)
- Chain Rule: \(\frac{d}{dx}f(g(x))=f'(g(x))\cdot g'(x)\)
- Exponential Derivatives: \(\frac{d}{dx}e^{g(x)}=e^{g(x)}\cdot g'(x)\)
\(e^{-1}[1-x]+3e^{3x}\)
Start with Quotient Rule, then Chain Rule to derive the top and bottom respectively.
- Product Rule: \(\frac{d}{dx}f(x)\cdot g(x)=f'(x)g(x)+f(x)g'(x)\)
- Quotient Rule: \(\frac{d}{dx} \frac{f(x)}{g(x)} = \frac{f'(x)g(x)-f(x)g'(x)}{[g(x)]^2}\)
- Chain Rule: \(\frac{d}{dx}f(g(x))=f'(g(x))\cdot g'(x)\)
- Exponential Derivatives: \(\frac{d}{dx}e^{g(x)}=e^{g(x)}\cdot g'(x)\)
\(\frac{2(x+1)(x-1)^3-3(x+1)^2(x-1)}{(x-1)^6}\) or \(\frac{2(x+1)(x-1)^2-3(x+1)^2}{(x-1)^5}\)
Start with Product Rule, followed by Chain Rule
- Product Rule: \(\frac{d}{dx}f(x)\cdot g(x)=f'(x)g(x)+f(x)g'(x)\)
- Quotient Rule: \(\frac{d}{dx} \frac{f(x)}{g(x)} = \frac{f'(x)g(x)-f(x)g'(x)}{[g(x)]^2}\)
- Chain Rule: \(\frac{d}{dx}f(g(x))=f'(g(x))\cdot g'(x)\)
- Exponential Derivatives: \(\frac{d}{dx}e^{g(x)}=e^{g(x)}\cdot g'(x)\)
\(-2(2x-5)^{-2}(x^2-x)^2+2(2x-5)^{-1}(x^2-x)(2x-1)\) or \(\frac{-2(x^2-x)^2}{(2x-5)^2}+\frac{2(x^2-x)(2x-1)}{(2x-5)}\)
Start with Quotient Rule, then Chain Rule to derive the top and bottom respectively.
- Product Rule: \(\frac{d}{dx}f(x)\cdot g(x)=f'(x)g(x)+f(x)g'(x)\)
- Quotient Rule: \(\frac{d}{dx} \frac{f(x)}{g(x)} = \frac{f'(x)g(x)-f(x)g'(x)}{[g(x)]^2}\)
- Chain Rule: \(\frac{d}{dx}f(g(x))=f'(g(x))\cdot g'(x)\)
- Exponential Derivatives: \(\frac{d}{dx}e^{g(x)}=e^{g(x)}\cdot g'(x)\)
\(e^{-2x}(x^2-5)^2\cdot [-2(x^2-5)+6x]\)
Start with Chain Rule, then Quotient Rule
- Product Rule: \(\frac{d}{dx}f(x)\cdot g(x)=f'(x)g(x)+f(x)g'(x)\)
- Quotient Rule: \(\frac{d}{dx} \frac{f(x)}{g(x)} = \frac{f'(x)g(x)-f(x)g'(x)}{[g(x)]^2}\)
- Chain Rule: \(\frac{d}{dx}f(g(x))=f'(g(x))\cdot g'(x)\)
- Exponential Derivatives: \(\frac{d}{dx}e^{g(x)}=e^{g(x)}\cdot g'(x)\)
\(\frac{35(3t+1)^{-6}}{(4t-1)^{-4}}\) or \(\frac{35(4t-1)^4}{(3t+1)^6}\)
Start with Chain Rule, followed by Quotient Rule
- Product Rule: \(\frac{d}{dx}f(x)\cdot g(x)=f'(x)g(x)+f(x)g'(x)\)
- Quotient Rule: \(\frac{d}{dx} \frac{f(x)}{g(x)} = \frac{f'(x)g(x)-f(x)g'(x)}{[g(x)]^2}\)
- Chain Rule: \(\frac{d}{dx}f(g(x))=f'(g(x))\cdot g'(x)\)
- Exponential Derivatives: \(\frac{d}{dx}e^{g(x)}=e^{g(x)}\cdot g'(x)\)
\(\frac{3x^6}{(x^3-4x)^4}\cdot (-3x^2+2x-7)\)
Start with Chain Rule, followed by Quotient Rule
- Product Rule: \(\frac{d}{dx}f(x)\cdot g(x)=f'(x)g(x)+f(x)g'(x)\)
- Quotient Rule: \(\frac{d}{dx} \frac{f(x)}{g(x)} = \frac{f'(x)g(x)-f(x)g'(x)}{[g(x)]^2}\)
- Chain Rule: \(\frac{d}{dx}f(g(x))=f'(g(x))\cdot g'(x)\)
- Exponential Derivatives: \(\frac{d}{dx}e^{g(x)}=e^{g(x)}\cdot g'(x)\)
\(\frac{(x-1)^{-\frac{1}{2}}}{(x+1)^{\frac{3}{2}}}\) or \(\frac{1}{(x-1)^{\frac{1}{2}}(x+1)^{\frac{3}{2}}}\)
Start with Quotient Rule, then Chain Rule to derive the bottom
- Product Rule: \(\frac{d}{dx}f(x)\cdot g(x)=f'(x)g(x)+f(x)g'(x)\)
- Quotient Rule: \(\frac{d}{dx} \frac{f(x)}{g(x)} = \frac{f'(x)g(x)-f(x)g'(x)}{[g(x)]^2}\)
- Chain Rule: \(\frac{d}{dx}f(g(x))=f'(g(x))\cdot g'(x)\)
- Exponential Derivatives: \(\frac{d}{dx}e^{g(x)}=e^{g(x)}\cdot g'(x)\)
\(\frac{(1-2x)^{\frac{1}{2}}+x(1-2x)^{-\frac{1}{2}}}{1-2x}\)
Start with Quotient Rule, then Chain Rule
- Product Rule: \(\frac{d}{dx}f(x)\cdot g(x)=f'(x)g(x)+f(x)g'(x)\)
- Quotient Rule: \(\frac{d}{dx} \frac{f(x)}{g(x)} = \frac{f'(x)g(x)-f(x)g'(x)}{[g(x)]^2}\)
- Chain Rule: \(\frac{d}{dx}f(g(x))=f'(g(x))\cdot g'(x)\)
- Exponential Derivatives: \(\frac{d}{dx}e^{g(x)}=e^{g(x)}\cdot g'(x)\)
\(\frac{\frac{1}{3}\cdot x (x^2-1)^{-\frac{2}{3}}-2(x^2-1)^{\frac{1}{3}}}{x^3}\)
Start with Quotient Rule, then Product Rule to derive the bottom
- Product Rule: \(\frac{d}{dx}f(x)\cdot g(x)=f'(x)g(x)+f(x)g'(x)\)
- Quotient Rule: \(\frac{d}{dx} \frac{f(x)}{g(x)} = \frac{f'(x)g(x)-f(x)g'(x)}{[g(x)]^2}\)
- Chain Rule: \(\frac{d}{dx}f(g(x))=f'(g(x))\cdot g'(x)\)
- Exponential Derivatives: \(\frac{d}{dx}e^{g(x)}=e^{g(x)}\cdot g'(x)\)
\(\frac{e^{2x}[x^2+\frac{1}{2}x^{\frac{1}{2}}-2x^3+2x^{\frac{3}{2}}]}{(xe^{2x})^2}\)
