Solving Logarithmic and Exponential Equations

A Brief Review of Cancellation

Recall from our log laws the following property.

That is, logs and exponential expressions sharing the same base cancel one another out, leaving you with whatever is inside either the exponent (for \(\log_a(a^x)=x\)) or inside the log (for \(a^{\log_a(x)}=x\)). Furthermore, this happens even when \(x\) is an algebraic expression! It doesn’t matter what sort of thing is there where \(x\) is.

---

Using Cancellation to Solve exponential Equations

The first part of the Log-Exponential Cancellation Property (i.e. \(\log_a(a^x)=x\)) and the one-to-one-ness of logarithmic functions enables us to solve equations where our variables are in the exponent of an exponential expression, such as in the equation

$$5^{3x-1}+3=10$$

Specifically, what we can do is get all our exponential expression stuff on one side of the equation, and then take logs of both sides… specifically, the log whole base is the same as the exponential expressions we see.

Using our above example, after subtracting \(3\) from both sides, we get

$$5^{3x-1}=7$$

Now, we take the \(\log_5\) of both sides so we can cancel out the base \(5\) of the exponential expression on the Left-Hand-Side

$$\begin{align}\log_5(5^{3x-1})&=\log_5(7)& \text{taking logs of both sides}\\ 3x-1&=\log_5(7)&\text{cancelled the log and the base of the power}\end{align}$$

Then, finally, after computing the value of \(\log_5(7)=1.2091\), and adding 1 to both sides of the equation and then dividing by 3, we get that

$$x=0.069687.$$

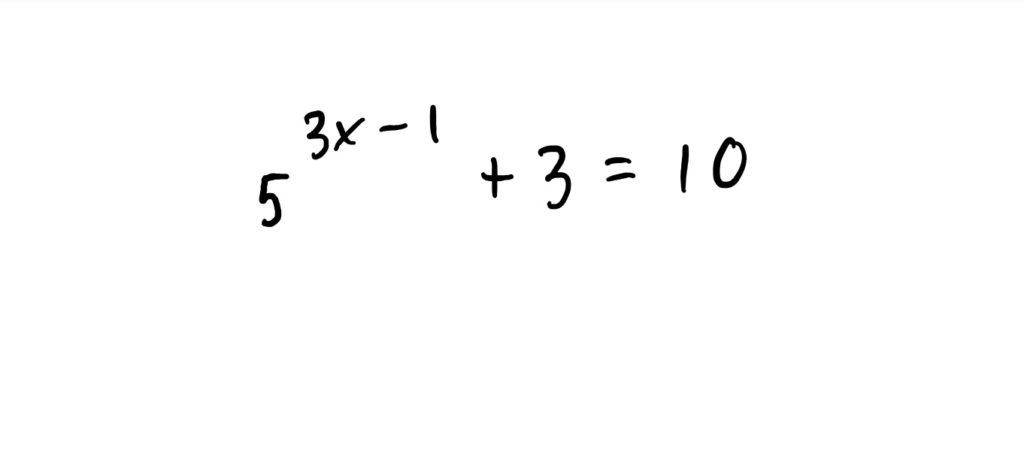
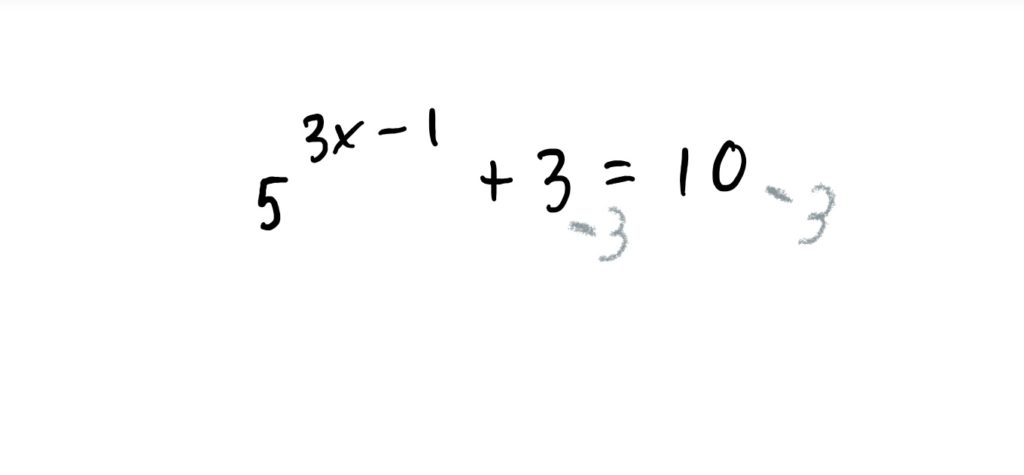
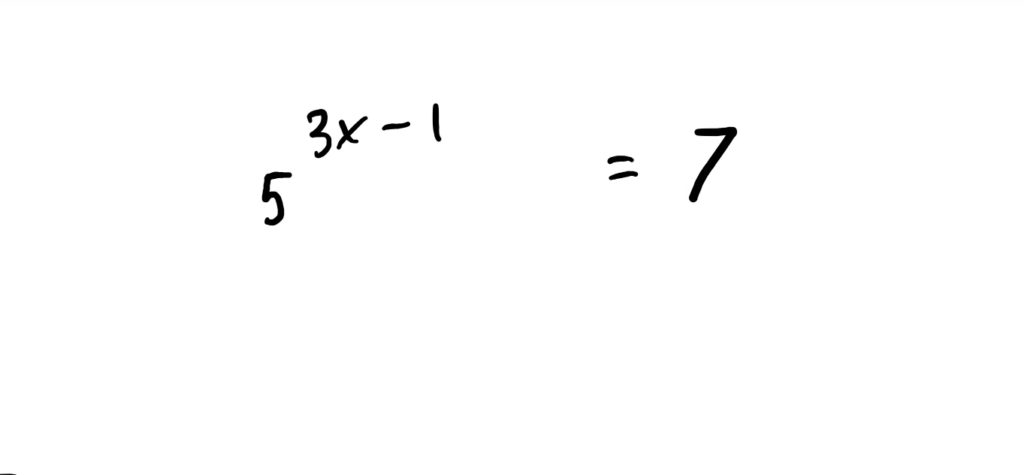
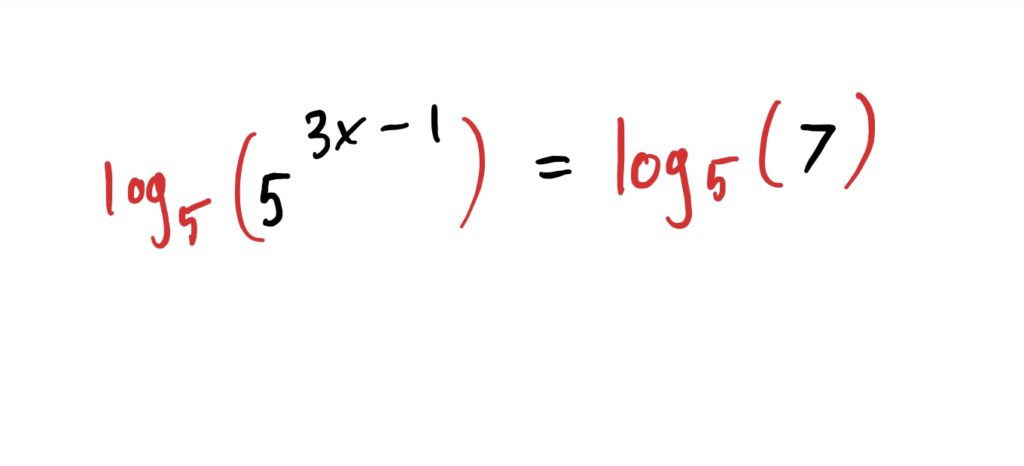
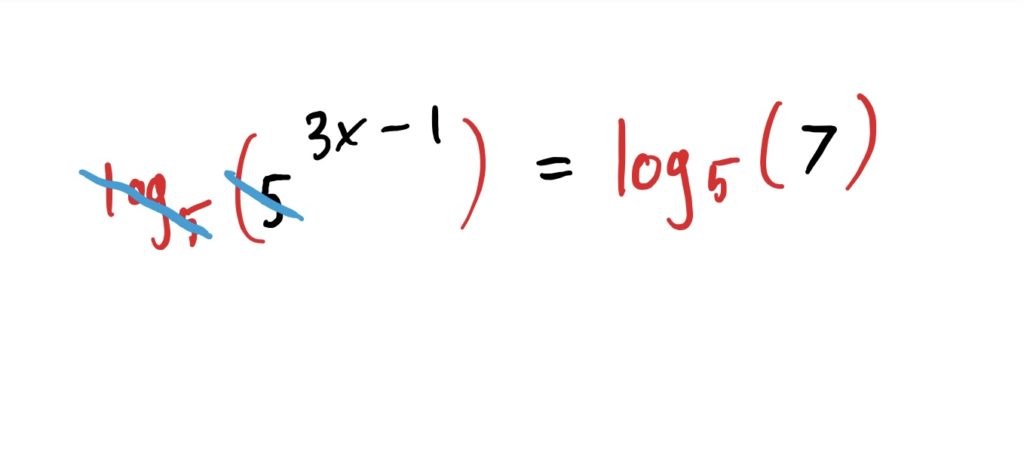
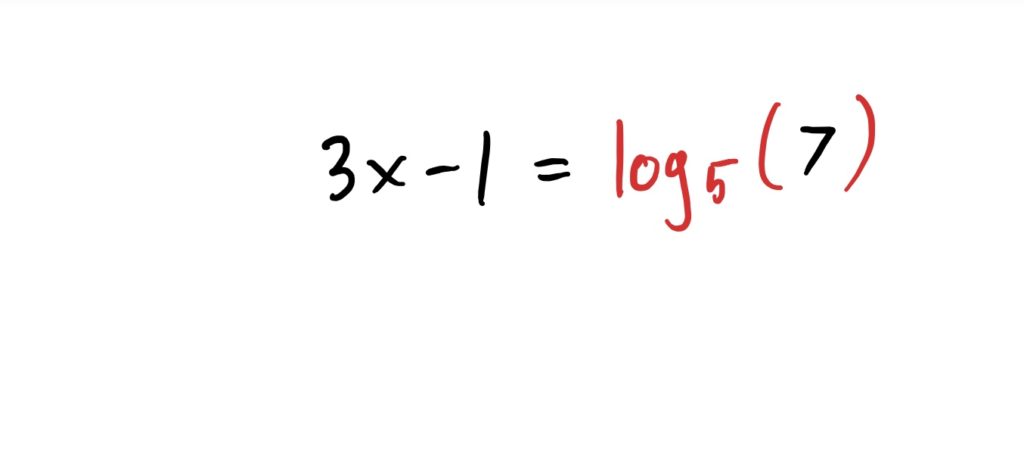
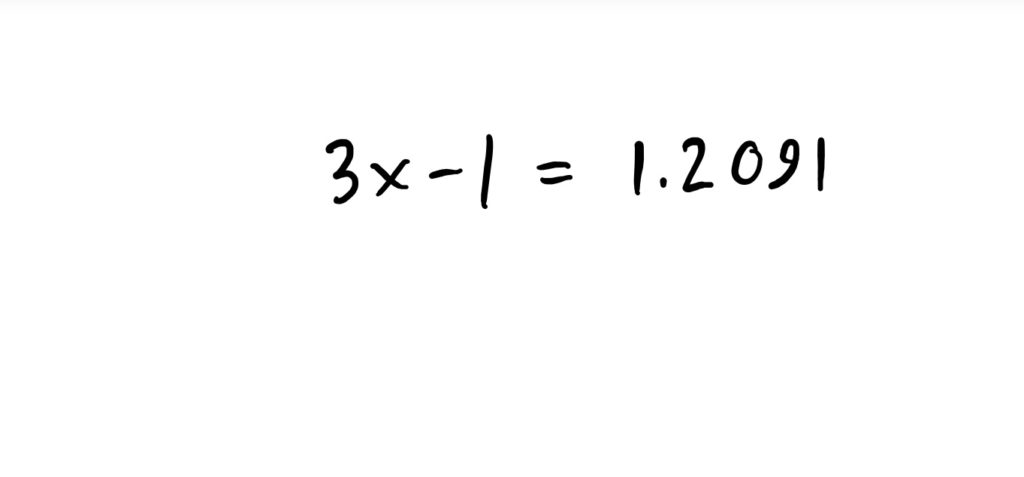
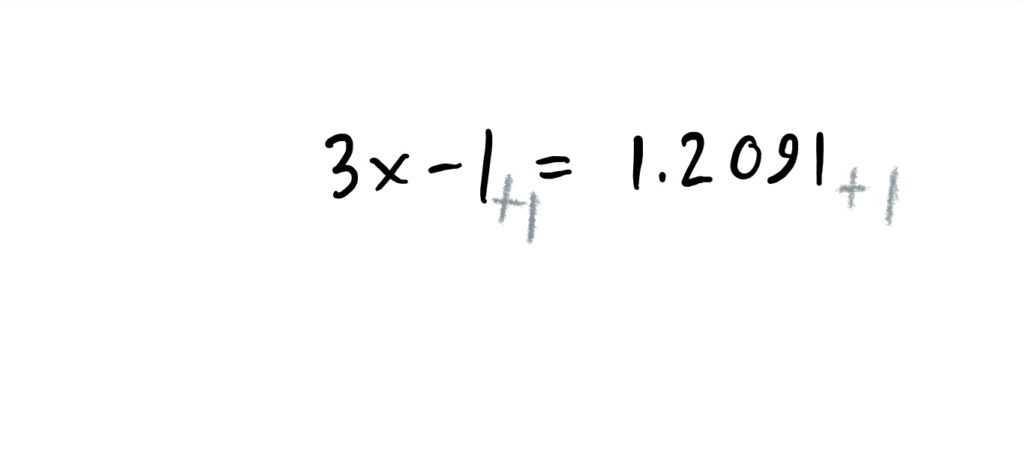
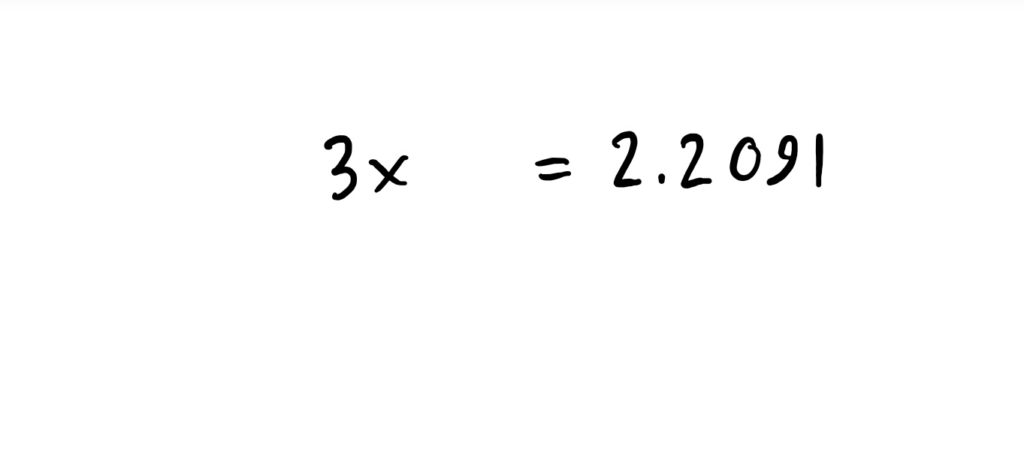
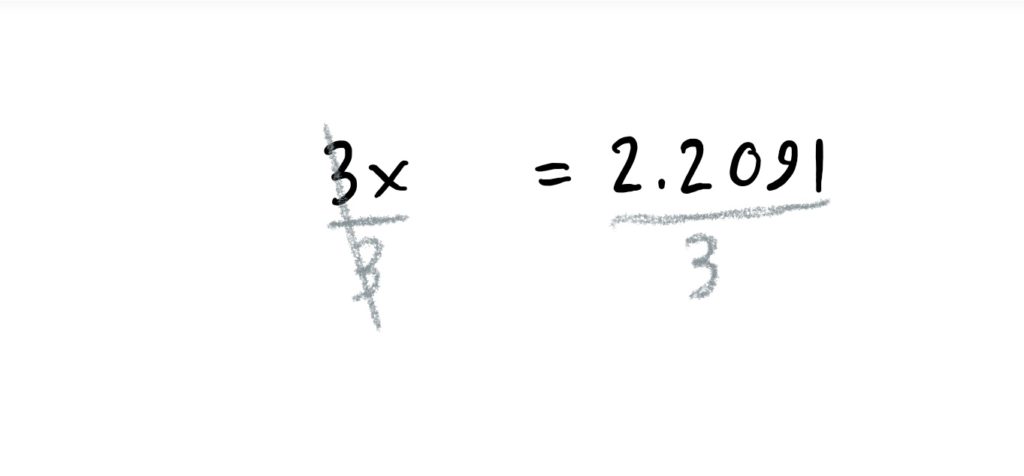
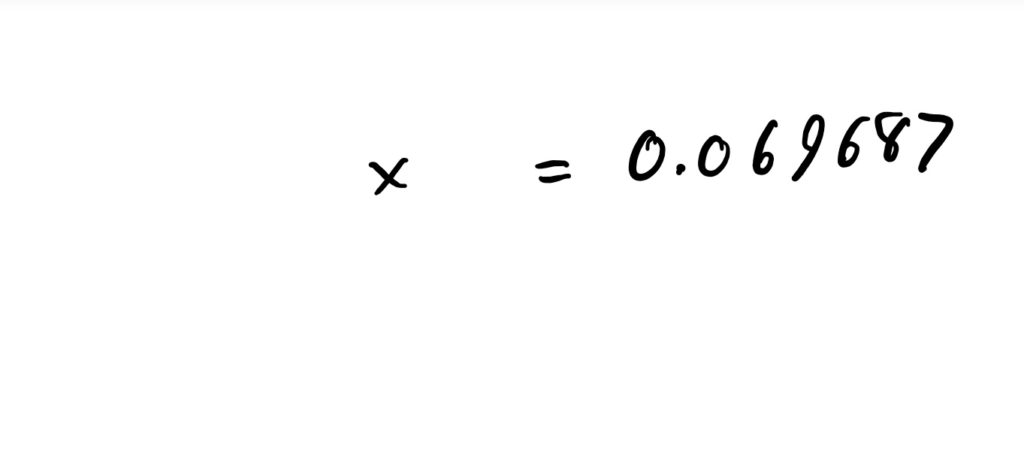
More complicated examples than this are explained in the examples section below. All things considered, the same exact idea/method applies in nearly every problem:

1. Simplify the equation and (usually) isolate the exponential expressions
2. Take logs of both sides (usually with the same base as the exponential expressions you see) and cancel the base with the log, leaving behind the exponent
3. Solve the equation for \(x\) using usual methods.

---

Solving Logarithmic Equations

Recall the second part of the Log-exponential cancellation property above:

$$a^{\log_a(x)}=x$$

This property is useful when you have equations involving logarithms of a certain base, like

$$\log_2(2x-1)=3$$

What we can do in these situations is use the one-to-one property of exponential functions, and exponentiate both sides of the equation, with base 2 (matching the log), in order to cancel the log. Viz:

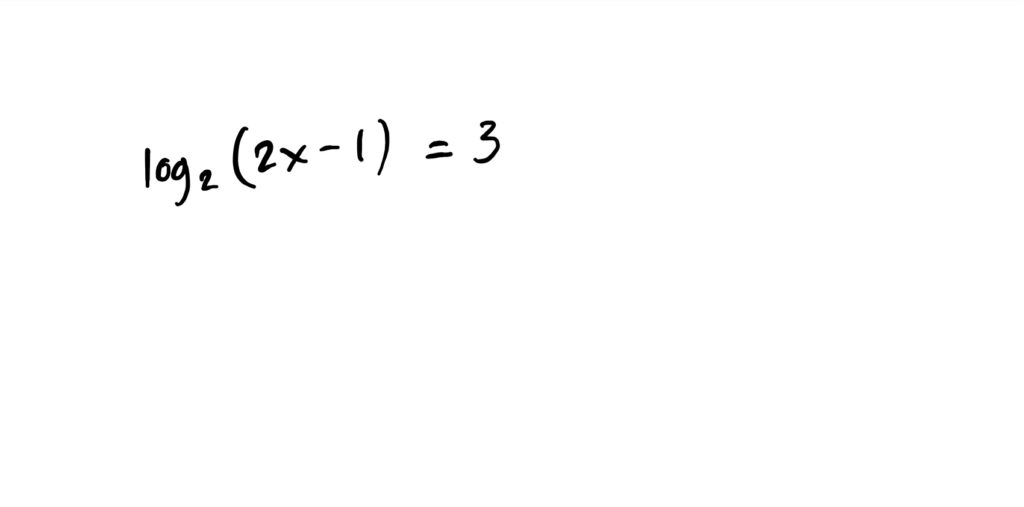
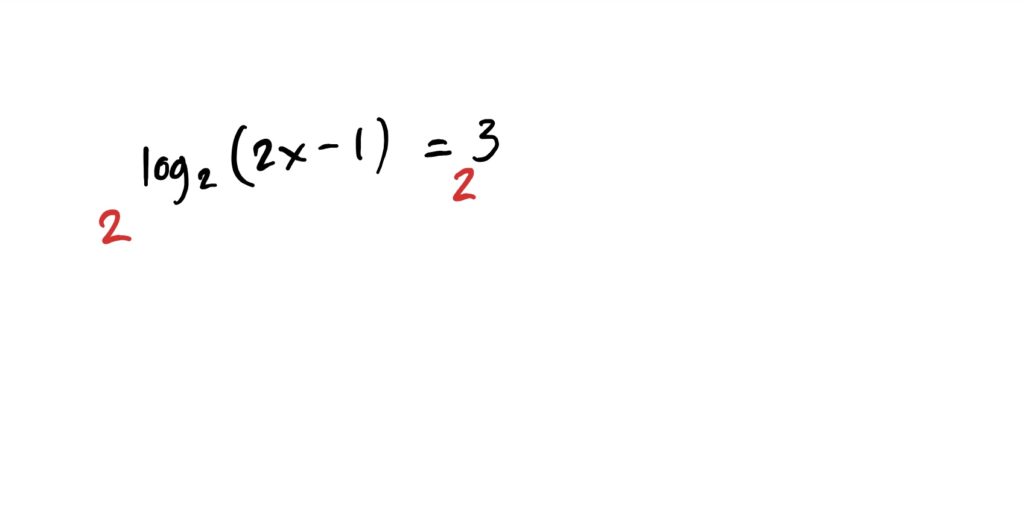
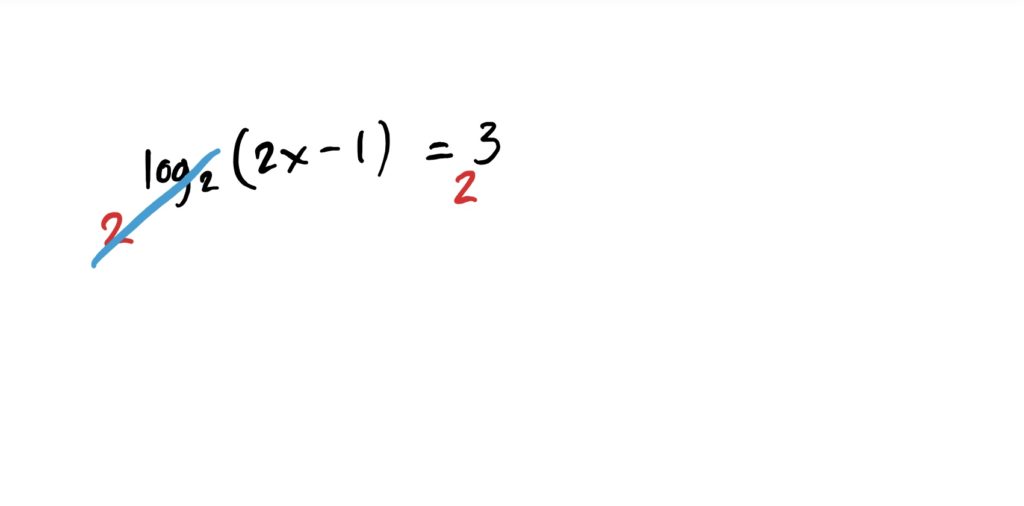
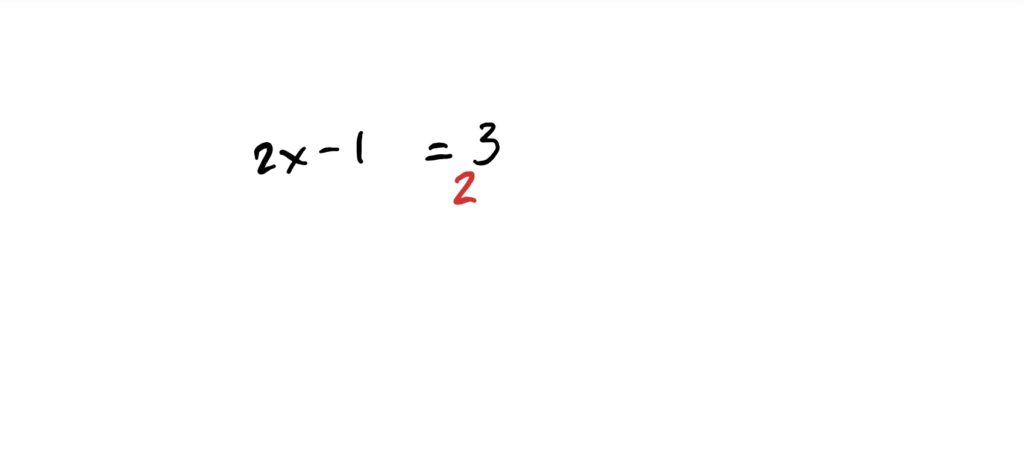
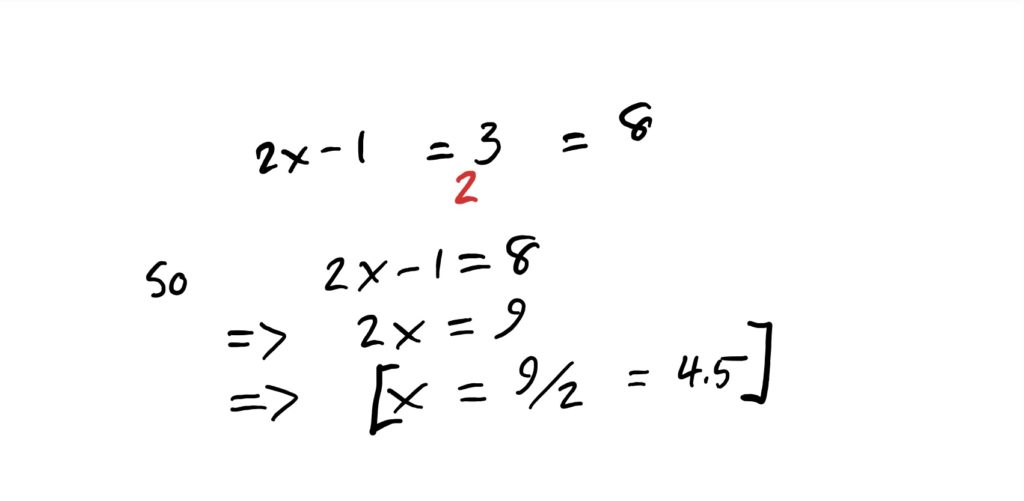
Naturally, these get a little more complicated and we will go over more complicated problems in the examples below. However even in those harder problems, the method largely remains invariant (unchanging):

1. Simplify the equation so that the logarithms are by themselves (Log laws help with this)
2. Exponentiate both sides using the same base as one of your logs.
3. Once all your logs are gone, solve the equation for \(x\) as you normally would.